Задачи на теоремы Менелая, Чевы и Стюарта. Формулы для биссектрисы и медианы

\(\blacktriangleright\) Теорема Менелая: пусть прямая пересекает треугольник в точке \(C_1\) на стороне \(AB\), в точке \(A_1\) на стороне \(BC\) и в точке \(B_1\) на продолжении стороны \(AC\). Тогда имеет место следующее соотношение:

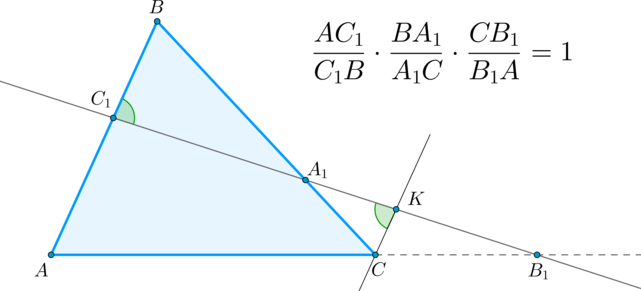
Доказательство: Проведем через точку \(C\) прямую параллельно \(AB\). Пусть она пересечет \(A_1B_1\) в точке \(K\). Тогда по двум углам \(\triangle A_1BC_1\sim \triangle A_1KC \Rightarrow\)

\(\dfrac{C_1B}{CK}=\dfrac{BA_1}{A_1C}\) или \(\dfrac{BA_1\cdot CK}{A_1C\cdot C_1B}=1 \ (*)\)

Т.к. \(\triangle AB_1C_1\sim \triangle CKB_1 \Rightarrow \)

\(\dfrac{CK}{AC_1}=\dfrac{B_1C}{AB_1}\), откуда \(CK=\dfrac{B_1C\cdot AC_1}{AB_1}\)

Подставив последнее равенство в \((*)\) и сгруппировав множители, получим требуемое равенство.

\(\blacktriangleright\) Теорема, обратная теореме Менелая: пусть в треугольнике точка \(B_1\) лежит на продолжении стороны \(AC\), а точки \(A_1, C_1\) — на сторонах \(BC\) и \(AB\) соответственно. Тогда, если выполнено равенство \[\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_1}{C_1A}=1,\] то точки \(A_1, B_1, C_1\) лежат на одной прямой.

Доказательство: Предположим, что эти три точки не лежат на одной прямой. Тогда прямая \(A_1B_1\) пересечет сторону \(AB\) в точке \(C_2\), отличной от точки \(C_1\). Тогда по теореме Менелая для точек \(A_1, B_1, C_2\) будет выполнено равенство:

\(\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_2}{C_2A}=1\)

Сравнивая это равенство с равенством из условия, получим, что \(\dfrac{BC_2}{C_2A}=\dfrac{BC_1}{C_1A}\),

то есть точки \(C_1\) и \(C_2\) поделили отрезок \(AB\) в одинаковом соотношении. Значит, эти точки совпадут.

Теорема Чевы: пусть на сторонах треугольника \(ABC\) выбраны точки \(A_1\in BC, B_1\in AC, C_1\in AB\). Отрезки \(AA_1, BB_1, CC_1\) пересекаются в одной точке тогда и только тогда, когда выполнено равенство \[{\large{\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_1}{C_1A}=1}}\]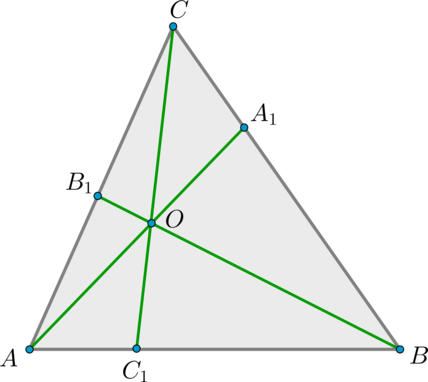

Доказательство:

1) Докажем, что из пересечения отрезков следует данное равенство:

Применим теорему Менелая для \(\triangle ABB_1\) и прямой \(CC_1\):

\(\dfrac{AC_1}{C_1B}\cdot \dfrac{BO}{OB_1}\cdot\dfrac{B_1C}{CA}=1\)

Применим теперь теорему Менелая для \(\triangle BB_1C\) и прямой \(AA_1\):

\(\dfrac{BA_1}{A_1C}\cdot \dfrac{CA}{AB_1}\cdot \dfrac{B_1O}{OB}=1\)

Перемножив полученные два равенства, получим:

\(\dfrac{AB_1}{B_1C}\cdot\dfrac{CA_1}{A_1B}\cdot\dfrac{BC_1}{C_1A}=1\)

2) Докажем, что из данного равенства следует, что отрезки пересекутся в одной точке:

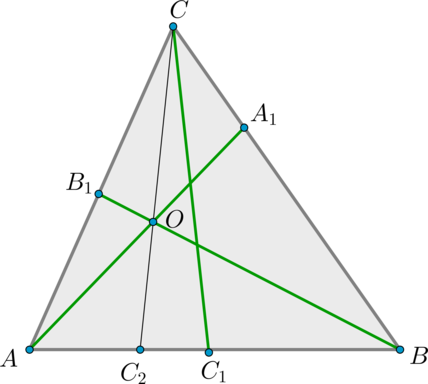
Предположим, что отрезок \(CC_1\) не проходит через точку \(O\). Тогда проведем отрезок \(CC_2\) через точку \(O\). Т.к. три отрезка \(AA_1, BB_1, CC_2\) пересеклись в одной точке, то для них верно:

\(\dfrac{AB_1}{B_1C}\cdot\dfrac{CA_1}{A_1B}\cdot\dfrac{BC_2}{C_2A}=1\)

Сравнивая полученное равенство с равенством из условия, заключаем, что

\(\dfrac{BC_2}{C_2A}=\dfrac{BC_1}{C_1A}\), т.е. точки \(C_1\) и \(C_2\) поделили отрезок \(AB\) в одинаковом отношении. Это возможно только в том случае, когда эти точки совпадают, т.е. \(C_1=C_2\).

\(\blacktriangleright\) Теорема Стюарта: пусть в треугольнике на стороне \(AB\) отмечена точка \(P\).
Тогда, если \(CP=p, AP=x, BP=y,AC=b, BC=a\), верно следующее соотношение:

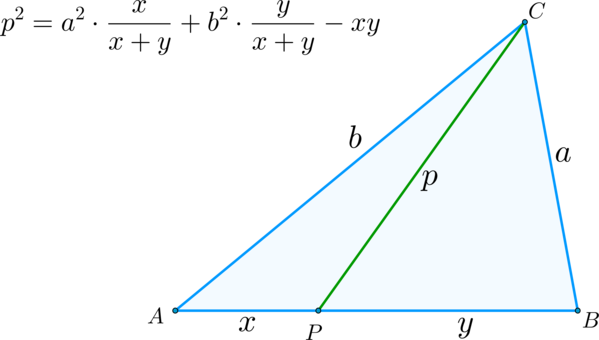
Доказательство: Рассмотрим \(\triangle ABC\): по теореме косинусов имеем
\(a^2=b^2+(x+y)^2-2b(x+y)\cos \angle A \Rightarrow \cos\angle A=\dfrac{b^2+(x+y)^2-a^2}{2b(x+y)}\)

Рассмотрим \(\triangle ACP\):
\(p^2=b^2+x^2-2bx\cos \angle A \Rightarrow \cos\angle A=\dfrac{b^2+x^2-p^2}{2bx}\)

Следовательно: \(\dfrac{b^2+x^2-p^2}{2bx}=\dfrac{b^2+(x+y)^2-a^2}{2b(x+y)} \Rightarrow \dfrac{b^2+x^2-p^2}{x}=\dfrac{b^2+(x+y)^2-a^2}{x+y}\), откуда получаем равенство из условия.

\(\blacktriangleright\) С помощью теоремы Стюарта выводятся формулы нахождения биссектрис и медиан треугольника:

I. Если \(l_c\) — биссектриса, проведенная к стороне \(c\) и разбивающая эту сторону на отрезки \(x\) и \(y\), а \(a,b\) — две другие его стороны, то \[{\large{l^2_c=ab-xy}}\]

Действительно, т.к. \(l_c\) — биссектриса, то она делит сторону \(c\) на отрезки, пропорциональные прилежащим сторонам, т.е.

\(\dfrac{x}{y}=\dfrac{b}{a}\)

Следовательно, можно принять \(x=kb, y=ka\), где \(k\) — этот коэффициент пропорциональности.

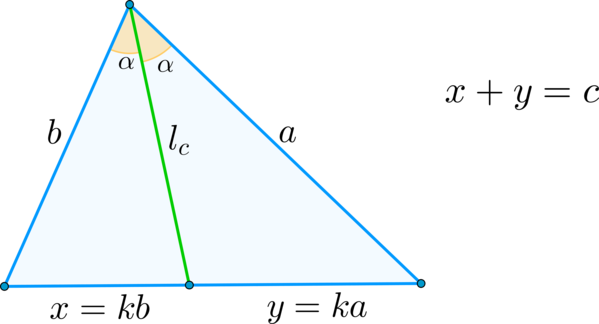
Запишем теорему Стюарта:

\(l^2_c=a^2\cdot \dfrac x{x+y}+b^2\cdot \dfrac y{x+y}-xy=\dfrac{a^2kb}{k(a+b)}+\dfrac{b^2ka}{k(a+b)}-xy=\dfrac{kab(a+b)}{k(a+b)}-xy=ab-xy\)

II. Если \(m_c\) — медиана, проведенная к стороне \(c\) треугольника, а \(a,b\) — две другие его стороны, то \[{\large{m^2_c=\dfrac{2a^2+2b^2-c^2}4}}\]

Действительно, т.к. \(m_c\) — медиана, то \(x=y\). Подставив это в равенство Стюарта, получим формулу вычисления медианы треугольника.