Теорема
В прямоугольной системе координат расстояние между точками \(P(x_1;
y_1)\) и \(Q(x_2; y_2)\) выражается формулой \(\rho(P, Q) = \sqrt{(x_1 -
x_2)^2 + (y_1 - y_2)^2}\).
Доказательство
Если \(PQ\parallel Ox\), то он лежит на некоторой прямой \(y = C\), тогда \(y_1 = y_2 = C\), следовательно, \(\sqrt{(x_1 - x_2)^2 + (y_1 -
y_2)^2} = |x_1 - x_2|\), что равно его длине.
Если \(PQ\parallel Oy\), то он лежит на некоторой прямой \(x = C\), тогда \(x_1 = x_2 = C\), следовательно, \(\sqrt{(x_1 - x_2)^2 + (y_1 -
y_2)^2} = |y_1 - y_2|\), что равно его длине.
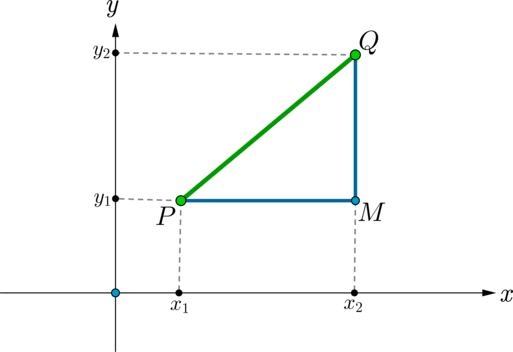
Если \(PQ\) не параллелен осям, то рассмотрим прямоугольный треугольник \(PQM\), в котором \(PM\parallel Ox\), \(QM\parallel Oy\). По теореме Пифагора \(PQ^2 = PM^2 + QM^2\). Так как \(PM\parallel Ox\), то \(PM\) лежит на некоторой прямой \(y = C\), откуда \(PM = |x_1 - x_2|\), аналогично \(QM = |y_1 - y_2|\), тогда \(PQ^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2\), откуда получаем требуемое равенство.
Утверждение
Если в прямоугольной системе координат точка \(M\) – середина отрезка \(PQ\), где \(P(x_1;y_1), \ Q(x_2;y_2)\), то
\[M\left(\dfrac{x_1 + x_2}{2}; \dfrac{y_1 +
y_2}{2}\right)\]
Доказательство
Пусть \(M(a;b)\).
1) Пусть \(PQ\parallel Oy \Rightarrow x_1=x_2=a\). Значит, \(a=\dfrac{x_1+x_2}2=\dfrac{a+a}2\) – верно.
Т.к. \(PM=MQ\), следовательно, \(|y_2-b|=|y_1-b| \Rightarrow
y_2-b=y_1-b\) или \(y_2-b=b-y_1\), что равносильно \(y_2=y_1\) или \(b=\dfrac{y_1+y_2}2\). Первое равенство невозможно (т.к. тогда точки \(P\) и \(Q\) совпадают).
2) Случай \(PQ\parallel Ox \Rightarrow y_1=y_2=b\) доказывается аналогично.
3) \(x_1\ne x_2, y_1\ne y_2\).
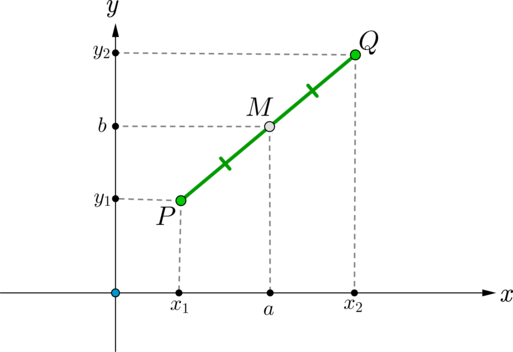
Тогда \(Ma=b\) – средняя линия трапеции \(x_1PQx_2\), следовательно, равна полусумме оснований, то есть \(b=\dfrac{y_1+y_2}2\).
Аналогично \(a=\dfrac{x_1+x_2}2\).
\[{\Large{\text{Векторы на координатной плоскости}}}\]
Лемма
Если векторы \(\overrightarrow a\) и \(\overrightarrow b\) коллинеарны, то существует такое число \(\lambda\ne 0\), что \(\overrightarrow
a=\lambda\overrightarrow b\).
Доказательство
1) Если \(\overrightarrow a\uparrow \uparrow \overrightarrow b\).
Рассмотрим вектор \(\dfrac1{|\overrightarrow a|}\overrightarrow a\). Данный вектор сонавправлен с \(\overrightarrow a\), а его длина равна \(1\). Тогда вектор \(\dfrac{|\overrightarrow b|}{|\overrightarrow
a|}\overrightarrow a\) также сонаправлен с \(\overrightarrow a\), но его длина равна \(|\overrightarrow b|\). То есть равен вектору \(\overrightarrow b\).
2) Если \(\overrightarrow a\uparrow \downarrow \overrightarrow b\).
Аналогично доказывается, что \(\overrightarrow
b=-\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow
a\).
Определение
Если вектор \(\overrightarrow p\) представлен как линейная комбинация двух векторов: \(\overrightarrow p=\alpha\overrightarrow a+\beta
\overrightarrow b\), то говорят, что вектор \(\overrightarrow p\) разложен по векторам \(\overrightarrow a\) и \(\overrightarrow b\).
\(\alpha, \beta\) – коэффициенты разложения.
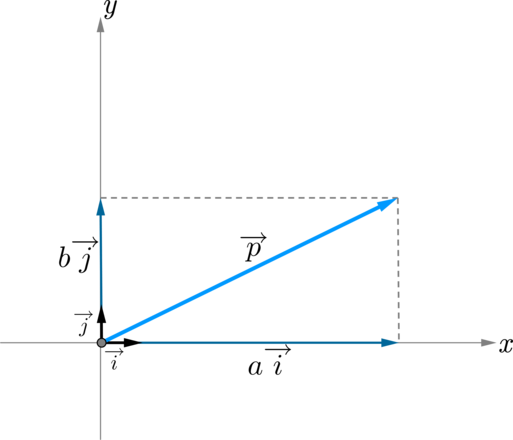
Пусть векторы \(\overrightarrow i\), \(\overrightarrow j\) – векторы, длины которых равны \(1\), а направление совпадает с направлением осей \(Ox\) и \(Oy\) соответственно. Такие векторы называются единичными векторами.
Тогда если \(\overrightarrow p=a\overrightarrow i+b\overrightarrow
j\), то \(\{a;b\}\) – координаты вектора \(\overrightarrow p\).
Свойства координат вектора
1. Равные векторы имеют равные координаты.
2. Координаты суммы векторов равны сумме координат каждого вектора: если \(\overrightarrow a\{x_1;y_1\}, \ \overrightarrow b\{x_2;y_2\}\), то \(\overrightarrow a+\overrightarrow b=\{x_1+x_2;y_1+y_2\}\).
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: \(\overrightarrow a\{x;y\}, \ \lambda \) – число, то \(\lambda\overrightarrow a\{\lambda x;\lambda y\}\).
Теорема
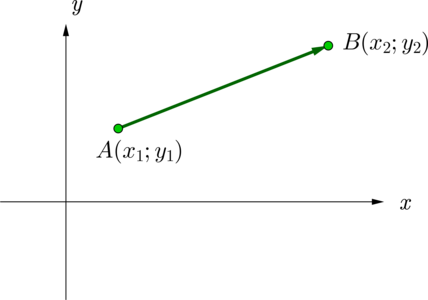
Если точки \(A(x_1;y_1), \ B(x_2;y_2)\), то \(\overrightarrow
{AB}\{x_2-x_1;y_2-y_1\}\).
То есть каждая координата вектора равна разности соответствующих координат его конца и начала.
Следствие
Если \(\overrightarrow a\{x;y\}\), то длина \(|\overrightarrow
a|=\sqrt{x^2+y^2}\).
\[{\Large{\text{Скалярное произведение векторов}}}\]
Определение
Пусть от одной точки отложены два вектора \(\overrightarrow {AB}\) и \(\overrightarrow {AC}\). Тогда угол между этими векторами – это угол \(\angle BAC\), не превышающий развернутого угла.

Скалярное произведение векторов \(\overrightarrow a\) и \(\overrightarrow b\) – это число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: \(\overrightarrow a\cdot \overrightarrow b\) или \((\overrightarrow a, \overrightarrow b)\). \[(\overrightarrow a, \overrightarrow b)=|\overrightarrow a|\cdot
|\overrightarrow b|\cdot \cos\widehat{(\overrightarrow a,
\overrightarrow b)}\]
Следствия
1. Если ненулевые векторы взаимно перпендикулярны, то косинус угла между ними равен нулю, следовательно, и их скалярное произведение равно нулю.
2. Если угол между ненулевыми векторами острый, то скалярное произведение положительно.
3. Если угол между ненулевыми векторами тупой, то скалярное произведение отрицательно.
4.Скалярное произведение вектора на себя равно квадрату его длины: \(\overrightarrow a\cdot \overrightarrow a=|\overrightarrow a|^2\).
Теорема
В прямоугольной системе координат скалярное произведение векторов \(\overrightarrow a\{x_1;y_1\}\) и \(\overrightarrow b\{x_2;y_2\}\) выражается формулой:
\[\overrightarrow a\cdot \overrightarrow b=x_1x_2+y_1y_2\]
Доказательство
Рассмотрим вектор \(\overrightarrow c\):
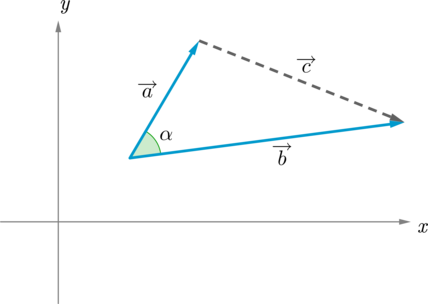
Т.к. \(\overrightarrow a+\overrightarrow c=\overrightarrow b
\Rightarrow \overrightarrow c=\overrightarrow b-\overrightarrow a
\Rightarrow \overrightarrow c \{x_2-x_1; y_2-y_1\}\).
По теореме косинусов: \(|c|^2=|a|^2+|b|^2-2|a||b|\cos\alpha\), но \(|a||b|\cos \alpha=\overrightarrow a\cdot \overrightarrow b\), значит: \[\overrightarrow a\cdot \overrightarrow b=\dfrac12\left(|a|^2+|b|^2-|c|^2\right)
=\dfrac12\left(x_1^2+y_1^2+x_2^2+y_2^2-(x_2-x_1)^2-(y_2-y_1)^2\right)=x_1x_2+y_1y_2\]
Свойства скалярного произведения
Для любых векторов \(\overrightarrow a, \overrightarrow b,
\overrightarrow c\) и любого числа \(\lambda\) справедливо:
1. Скалярное произведение вектора на себя всегда неотрицательно, причем равно нулю оно тогда и только тогда, когда вектор нулевой: \(\overrightarrow a^2\geqslant 0, \quad \overrightarrow a^2=0
\Leftrightarrow |\overrightarrow a|=0\).
2. Переместительный закон: \(\overrightarrow a\cdot \overrightarrow
b=\overrightarrow b\cdot \overrightarrow a\).
3. Распределительный закон: \(\overrightarrow a \cdot
(\overrightarrow b+\overrightarrow c)=\overrightarrow a\cdot
\overrightarrow b+\overrightarrow a\cdot \overrightarrow c\).
4. Сочетательный закон: \((\lambda\overrightarrow a)\cdot
\overrightarrow b=\lambda (\overrightarrow a\cdot \overrightarrow
b)\).









