2. Площадь многоугольника, составленного из нескольких многоугольников, у которых внутренние области не пересекаются, равна сумме площадей этих многоугольников.

Определение

Площадь квадрата – это число, равное квадрату длины его стороны.

Площади многоугольников*
Данные формулы были рассмотрены в разделе “Геометрия на плоскости. Часть I” в теме “Площади многоугольников”.

Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию.

Площадь треугольника равна \(\sqrt{p(p-a)(p-b)(p-c)}\), где \(a, b, c\) — его стороны, а \(p\) – полупериметр.

Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию.

Площадь прямоугольника равна произведению длин двух его смежных сторон.

Площадь ромба равна половине произведения его диагоналей.

Площадь квадрата равна половине квадрата длины его диагонали.

Площадь трапеции равна произведению ее высоты на полусумму оснований.

Замечание

В школьном курсе геометрии понятие площади базируется на понятии длины. Попробуйте сформулировать, что такое длина отрезка?

Теорема: площадь треугольника

Площадь треугольника равна половине произведения его сторон на синус угла между ними.

Доказательство

Рассмотрим треугольник \(ABC\) и проведем в нем высоту \(BH\).

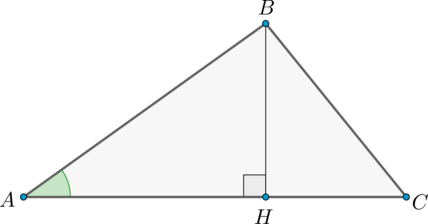
Тогда \(S_{\triangle ABC}=\dfrac 12 BH\cdot AC \qquad (*)\).

Из прямоугольного треугольника \(ABH\): \(\sin \angle A=\dfrac{BH}{AB} \Rightarrow BH=AB\cdot \sin \angle A\). Подставим данное выражение в формулу \((*)\):

\(S_{\triangle ABC}=\dfrac 12 AB\cdot AC\cdot \sin \angle A\), чтд.

Теорема: площадь параллелограмма

Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними.

Доказательство

Рассмотрим параллелограмм \(ABCD\) и проведем диагональ \(BD\). Треугольники \(ABD\) и \(CBD\) равны по трем сторонам.

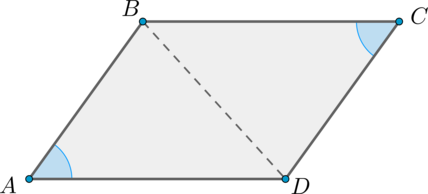
Следовательно, \(S_{ABCD}=2S_{ABD}=2\cdot \dfrac12 AB\cdot AD\cdot \sin\angle A=AB\cdot AD\cdot \sin\angle A\), чтд.

Теорема

Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Доказательство

Рассмотрим выпуклый четырехугольник \(ABCD\). Обозначим \(AO=a, BO=b, CO=c, DO=d\).

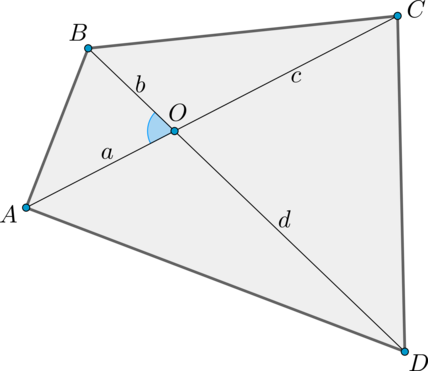
Заметим, что \(\angle AOB\) и \(\angle BOC\) — смежные, следовательно, \(\sin \angle AOB=\sin \angle BOC\).

Заметим также, что \(\angle AOB\) и \(\angle COD\), \(\angle BOC\) и \(\angle DOA\) – пары вертикальных углов, следовательно, они равны, следовательно, и их синусы равны.

Таким образом, обозначим \(\sin \angle AOB=\sin \angle BOC=\sin \angle COD=\sin \angle DOA=\sin \angle O\).

\(\begin{multline*} S_{ABCD}=S_{AOB}+S_{BOC}+S_{COD}+S_{DOA}=\\ =\frac 12 ab\cdot\sin \angle O+\frac12 bc\cdot\sin \angle O+\frac 12cd\cdot\sin \angle O+\frac12 da\cdot\sin \angle O= \frac12 \sin \angle O(ab+bc+cd+da)=\\ =\frac12 \sin \angle O(b(a+c)+d(a+c))= \frac12 \sin \angle O(a+c)(b+d)=\frac12 AC\cdot BD\cdot \sin \angle O \end{multline*}\)