\(\blacktriangleright\) На ОДЗ верны следующие формулы:
\[\large{\begin{array}{|ll|}
\hline a^0=1 &a^1=a\\
a^{nm}=(a^n)^m &a^n\cdot a^m=a^{n+m}\\
\dfrac{a^n}{a^m}=a^{n-m}&a^{-n}=\dfrac{1}{a^n}\\
a^n\cdot b^n=(a\cdot b)^n &\\
a^{\frac{k}{r}}=\sqrt[r]{a^k} \qquad \qquad \qquad \qquad&
\dfrac{a^n}{b^n}=\left(\dfrac{a}{b}\right)^n\\&\\
a,b>0, \ \ a,b\ne 1, \ k\in \mathbb{Z},& r\in\mathbb{N}, \ m,n\in\mathbb{R}\\
\hline
\end{array}}\]
\(\blacktriangleright\) Стандартное показательное неравенство: \[{\Large{a^{h(x)}\geqslant a^{g(x)} \ (*)}}\] где \(a>0,\ a\ne 1\)
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
Показательная функция \(f(x)=a^x\) является возрастающей, если число \(a>1\), и убывающей, если \(0<a<1\), и определена при всех \(x\) (то есть ее область определения \(x\in\mathbb{R}\)).
На графике приведен пример возрастающей показательной функции \(f_1(x)=2^x\) и убывающей показательной функции \(f_2(x)=(0,5)^x\).
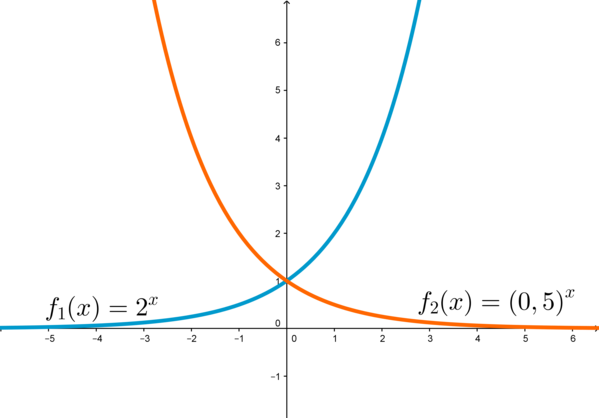
Напомним, что функция возрастает, если при увеличении \(x\) увеличивается и \(f(x)\). Функция убывает, если при увеличении \(x\) уменьшается \(f(x)\).
Действительно, для функции \(f_1(x)=2^x\), например, \(f_1(2)>f_1(3)
\Leftrightarrow 4>8\), а для функции \(f_2(x)=0,5^x\), например, \(f_2(2)<f_2(3) \Leftrightarrow 0,25<0,125\).
Таким образом, неравенство \((*)\) есть не что иное, как сравнение \(f(h)\) и \(f(g)\). Если функция \(f\) — возрастает, то неравенство \(f(h)\geqslant f(g)\) равносильно неравенству \(h\geqslant g\), а если убывает — то неравенству \(h\leqslant g\).
Поэтому для того, чтобы решить неравенство \((*)\), нужно сравнить основание \(a\) с единицей:
если \({\large{a>1}}\), то данное неравенство равносильно \[{\Large{h(x)\geqslant g(x)}}\]
если \({\large{0<a<1}}\), то данное неравенство равносильно \[{\Large{h(x)\leqslant g(x)}}\]
\(\blacktriangleright\) Напомним, что область значений показательной функции — все положительные числа, т.е. \(a^x>0\) при всех возможных \(a\) и \(x\).
\(\blacktriangleright\) С помощью формулы \({\Large{b=a^{\log_ab}}}\) можно любое число \(b>0\) представить в виде степени необходимого нам числа \(a>0,\ a\ne 1\).
Пример 1. Решить неравенство \(2^x>3^{x-1}\).
Нужно представить левую и правую части неравенства как степени с одинаковым основанием. Воспользовавшись формулой, можно записать \(3=2^{\log_23}\). Тогда неравенство примет вид:
\(2^x>2^{\log_23\cdot (x-1)}\). Т.к. основания \(2>1\), то знак неравенства не будет меняться и данное неравенство равносильно неравенству
\(x>\log_23\cdot (x-1)\). Отсюда \((1-\log_23)x>-\log_23\). Т.к. \(\log_23>1\), то \((1-\log_23)<0\), значит, при делении правой и левой частей неравенства на \((1-\log_23)\) нужно изменить знак неравенства на противоположный, то есть \[x<-\dfrac{\log_23}{1-\log_23}
\Leftrightarrow x<\dfrac{\log_23}{\log_23-1}\].
\(\blacktriangleright\) Рассмотрим неравенства вида \[{\Large{(f(x))^{h(x)}\lor(f(x))^{g(x)}}}\] то есть когда в основании находится не конкретное число, а функция, также зависящая от \(x\).
В таких неравенствах \(f(x)\) может быть равно единице, если знак неравенства нестрогий (т.е. \(\geqslant, \ \leqslant\)) и если это не противоречит ОДЗ неравенства. Действительно, тогда мы получаем, например, \(1^{h(x)}\geqslant 1^{g(x)}\), что верно, т.к. единица в любой степени дает единицу.
Таким образом, имеем: \[\textbf{I. }{\Large{(f(x))^{h(x)}> (f(x))^{g(x)} \quad \Leftrightarrow\quad \left[\begin{gathered}
\begin{aligned}
&\begin{cases} f(x)>1\\ h(x)>
g(x) \end{cases}\\[2pt]
&\begin{cases} 0<f(x)<1\\ h(x)< g(x) \end{cases}
\end{aligned}
\end{gathered}
\right.}}\]
\[\textbf{II. }{\Large{(f(x))^{h(x)}\geqslant (f(x))^{g(x)}
\quad\Leftrightarrow\quad \left[\begin{gathered}
\begin{aligned}
&\begin{cases} f(x)>1\\ h(x)\geqslant
g(x) \end{cases}\\[2pt]
&\begin{cases} 0<f(x)<1\\ h(x)\leqslant g(x) \end{cases}\\[2pt]
&f(x)=1
\end{aligned}
\end{gathered}
\right.}}\]
Пример 2. Решить неравенство \(x^{\sqrt{x-0,5}}\geqslant x^2\)
Запишем ОДЗ: выражение под корнем должно быть неотрицательным, т.е. \(x-0,5\geqslant 0 \Leftrightarrow x\geqslant
0,5\). Тогда на ОДЗ данное неравенство равносильно:
\(\left[\begin{gathered}
\begin{aligned}
&\begin{cases} x>1\\ \sqrt{x-0,5}\geqslant
2 \end{cases}\\[2pt]
&\begin{cases} 0<x<1\\ \sqrt{x-0,5}\leqslant 2 \end{cases}\\[2pt]
&x=1
\end{aligned}
\end{gathered}
\right. \Rightarrow \left[\begin{gathered}
\begin{aligned}
&\begin{cases} x>1\\ x\geqslant
4,5 \end{cases}\\[2pt]
&\begin{cases} 0<x<1\\ x\leqslant 4,5 \end{cases}\\[2pt]
&x=1
\end{aligned}
\end{gathered}
\right. \Rightarrow x\in (0;1]\cup [4,5;+\infty)\)
Пересекая полученный ответ с ОДЗ, получим \[x\in
[0,5;1]\cup [4,5;+\infty)\]




