\({\color{red}{\textbf{Факт 1. Про векторы}}}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), то вектор \(\overrightarrow{AB}\) имеет координаты \[\overrightarrow{AB} = \{x_2-x_1;y_2-y_1;z_2-z_1\}\]
\(\bullet\) Если в пространстве заданы два вектора \(\vec{a}
=\{x_1;y_1;z_1\}\) и \(\vec{b}=
\{x_2;y_2;z_2\}\), то:
\(\qquad \blacktriangleright\) сумма этих векторов \(\vec{a}+\vec{b}=\{x_1+x_2;y_1+y_2;z_1+z_2\}\)
\(\qquad \blacktriangleright\) разность этих векторов \(\vec{a}-\vec{b}=\{x_1-x_2;y_1-y_2;z_1-z_2\}\)
\(\qquad \blacktriangleright\) произведение вектора на число \(\lambda
\vec{a}=\{\lambda x_1;\lambda
y_1;\lambda z_1\}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), а точка \(O\) — середина отрезка \(AB\), то \(O\) имеет координаты \[O\left(\dfrac{x_1+x_2}2;\dfrac{y_1+y_2}2;\dfrac{z_1+z_2}2\right)\]
\(\bullet\) Длина вектора \(\vec{a}=\{x;y;z\}\) обозначается \(|\vec{a}|\) и вычисляется по формуле \[|\vec{a}|=\sqrt{x^2+y^2+z^2}\]
\(\bullet\) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
\({\color{red}{\textbf{Факт 2. Про скалярное произведение}}}\)
\(\bullet\) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: \[{\large{(\vec{a},
\vec{b})=|\vec{a}|\cdot|\vec{b}|\cdot\cos \angle (\vec{a},
\vec{b})}}\] На рисунке показано, что такое угол между векторами:
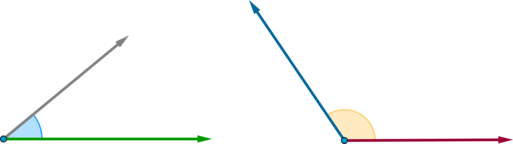
\(\bullet\) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: \[(\vec{a}, \vec{b})=0 \quad\Leftrightarrow\quad
\vec{a}\perp \vec{b}\]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: \[|\vec{a}|=\sqrt{(\vec{a},
\vec{a})}\]
III. Переместительный закон: \[(\vec{a}, \vec{b})=(\vec{b},
\vec{a})\]
IV. Распределительный закон: \[(\vec{a}+\vec{b},
\vec{c})=(\vec{a}, \vec{c})+(\vec{b}, \vec{c})\]
V. Сочетательный закон (\(\lambda\) – число): \[\lambda(\vec{a}, \vec{b})=(\lambda
\vec{a}, \vec{b})\]
\(\bullet\) Скалярное произведение двух векторов \(\vec{a}
=\{x_1;y_1;z_1\}\) и \(\vec{b}= \{x_2;y_2;z_2\}\) можно вычислить с помощью координат этих векторов: \[{\large{(\vec{a},
\vec{b})=x_1x_2+y_1y_2+z_1z_2}}\]
\(\bullet\) Косинус угла между векторами \(\vec{a} =\{x_1;y_1;z_1\}\) и \(\vec{b}= \{x_2;y_2;z_2\}\) вычисляется по формуле: \[{\large{\cos\angle(\vec{a}, \vec{b})=\dfrac{x_1x_2+y_1y_2+z_1z_2}
{\sqrt{x^2_1+y^2_1+z^2_1}\cdot
\sqrt{x^2_2+y^2_2+z^2_2}}}}\]
\({\color{red}{\textbf{Факт 3. Про уравнение плоскости}}}\)
\(\bullet\) Если \(\vec{n}=\{a;b;c\}\) – нормаль к плоскости, то уравнение плоскости имеет вид \[ax+by+cz+d=0\] Для того, чтобы найти \(d\), нужно подставить в уравнение плоскости вместо \(x, y, z\) координаты любой точки, лежащей в этой плоскости.
Пример: если \(\vec{n}=\{1;2;3\}\) – нормаль к плоскости, \(O(4;5;6)\) – точка из плоскости, то справедливо: \(1\cdot 4+2\cdot 5+3\cdot
6+d=0\), откуда \(d=-32\), следовательно, уравнение плоскости имеет вид \(x+2y+3z-32=0\).
\(\bullet\) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть \(A(1;0;0), \
B(0;3;4), \ C(2;0;5)\) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: \[\begin{cases}
1\cdot a+0\cdot b+0\cdot c+d=0\\
0\cdot a+3\cdot b+4\cdot c+d=0\\
2\cdot a+0\cdot b+5\cdot c+d=0\end{cases} \quad\Rightarrow\quad
\begin{cases}
d=-a\\
3b+4c-a=0\\
a+5c=0\end{cases}\quad\Rightarrow\quad \begin{cases} d=-a\\
a=-5c\\
b=-3c\end{cases}\quad\Rightarrow\quad\begin{cases}a=-5c\\
b=-3c\\
d=5c\end{cases}\] Следовательно, уравнение плоскости имеет вид: \[-5c\cdot x-3c\cdot y+c\cdot z+5c=0\] Можно разделить обе части на \(c\), так как \(c\ne 0\) (иначе \(a=b=c=d=0\)), следовательно, уравнение плоскости имеет вид \[-5x-3y+z+5=0\]
\({\color{red}{\textbf{Факт 4. Про углы между прямыми, плоскостями}}}\)
\(\bullet\) Если векторы \(\vec{a} =\{x_1;y_1;z_1\}\) и \(\vec{b}=
\{x_2;y_2;z_2\}\) являются направляющими прямых \(p\) и \(q\), то косинус угла между этими прямыми равен: \[\cos \phi=\dfrac{|x_1x_2+y_1y_2+z_1z_2|}
{\sqrt{x^2_1+y^2_1+z^2_1}\cdot \sqrt{x^2_2+y^2_2+z^2_2}}\]
\(\bullet\) Если \(\vec{a}\) — направляющий вектор прямой \(p\), а \(\vec{n}\) — нормаль к плоскости \(\phi\) (перпендикуляр к плоскости), то синус угла между прямой \(p\) и плоскостью \(\phi\) равен модулю косинуса угла между векторами \(\vec{a}\) и \(\vec{n}\): \[\sin
\angle(p, \phi)=|\cos \angle(\vec{a}, \vec{n})|\]
\(\bullet\) Если две плоскости заданы уравнениями \(a_1x+b_1y+c_1z+d_1=0\) и \(a_2x+b_2y+c_2z+d_2=0\), то косинус угла между плоскостями ищется по формуле: \[{\large{\cos \phi=\left| \dfrac{a_1a_2+b_1b_2+c_1c_2}
{\sqrt{a^2_1+b^2_1+c^2_1}\cdot
\sqrt{a^2_2+b^2_2+c^2_2}}\right|}}\]
\({\color{red}{\textbf{Факт 5. Про расстояния от точки до плоскости,
между скрещивающимися прямыми}}}\)
\(\bullet\) Если \(M(x_0;y_0;z_0)\) — некоторая точка вне плоскости \(\phi\), \(ax+by+cz+d=0\) — уравнение плоскости \(\phi\), то расстояние от точки \(M\) до плоскости \(\phi\) ищется по формуле: \[\rho(M, \phi)=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\]
\(\bullet\) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.




