\(\blacktriangleright\) Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат.
Угол в \(1^\circ\) — это такой центральный угол, который опирается на дугу, длина которой равна \(\dfrac1{360}\) длины всей окружности.
\(\blacktriangleright\) Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси \(Ox\) (на рисунке выделено красным).
На рисунке таким образом отмечены углы \(45^\circ,\ 180^\circ,\
240^\circ\):
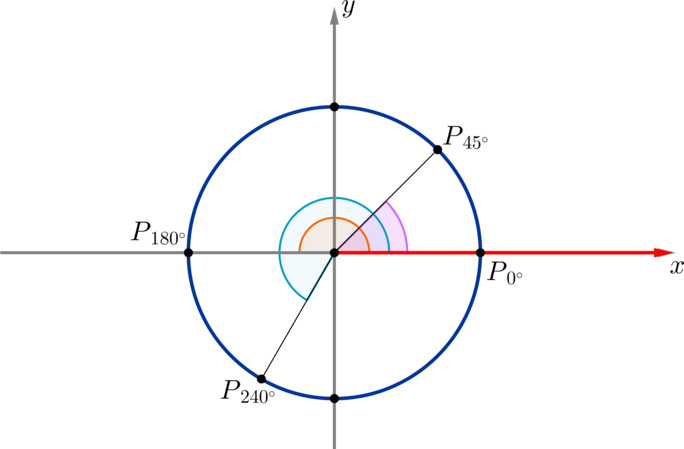
Заметим, что угол \(0^\circ\) — это угол, обе стороны которого совпадают с положительным направлением оси \(Ox\).
Точку, в которой вторая сторона такого угла \(\alpha\) пересекает окружность, будет называть \(P_{\alpha}\).
Положение точки \(P_{0}\) будем называть начальным положением.
Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения \(P_0\) до положения \(P_{\alpha}\) на угол \(\alpha\).
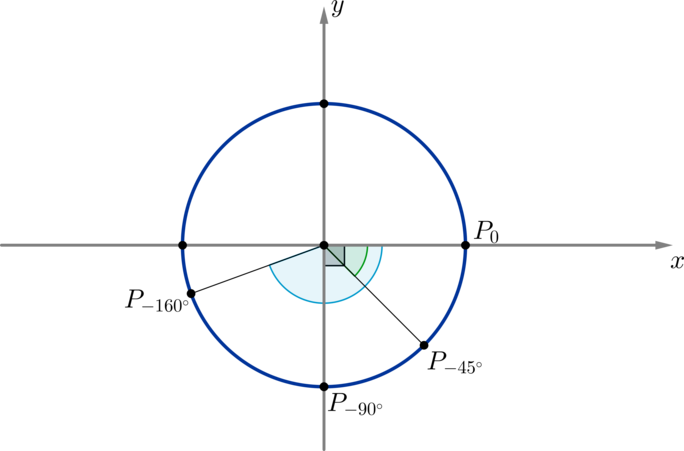
\(\blacktriangleright\) Поворот по окружности против часовой стрелки — это поворот на положительный угол. Поворот по часовой стрелке — это поворот на отрицательный угол.
Например, на рисунке отмечены углы \(-45^\circ, -90^\circ,
-160^\circ\):
\(\blacktriangleright\) Рассмотрим точку \(P_{30^\circ}\) на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки \(P_{30^\circ}\), необходимо совершить поворот на угол \(30^\circ\) (оранжевый). Если мы совершим полный оборот (то есть на \(360^\circ\)) и еще поворот на \(30^\circ\), то мы снова попадем в эту точку, хотя уже был совершен поворот на угол \(390^\circ=360^\circ+30^\circ\) (голубой). Также попасть в эту точку мы можем, совершив поворот на \(-330^\circ\) (зеленый), на \(750^\circ=360^\circ+360^\circ+30^\circ\) и т.д.
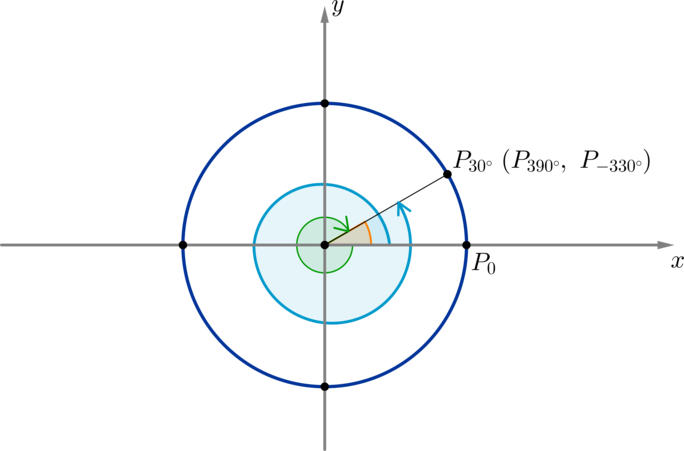
Таким образом, каждой точке на окружности соответствует бесконечное множество углов, причем отличаются эти углы друг от друга на целое число полных оборотов (\(n\cdot360^\circ, n\in\mathbb{Z}\)).
Например, угол \(30^\circ\) на \(360^\circ\) больше, чем угол \(-330^\circ\), и на \(2\cdot 360^\circ\) меньше, чем угол \(750^\circ\).
Все углы, находящиеся в точке \(P_{30^\circ}\) можно записать в виде: \(\alpha=30^\circ+n\cdot 360^\circ, \ n\in\mathbb{Z}\).
\(\blacktriangleright\) Угол в \(1\) радиан — это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности:
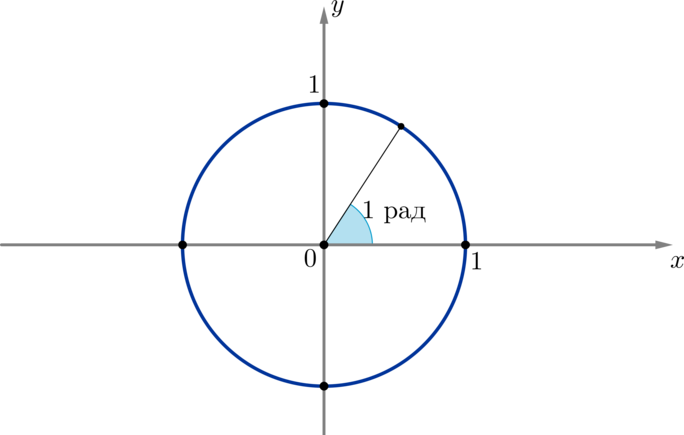
Т.к. длина всей окружности радиусом \(R\) равна \(2\pi R\), а в градусной мере — \(360^\circ\), то имеем \(360^\circ=2\pi \cdot
1\textbf{ рад}\), откуда \[180^\circ=\pi \textbf{ рад}\] Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот.
Пример 1. Найти радианную меру угла \(60^\circ\).
Т.к. \(180^\circ = \pi \Rightarrow 1^\circ = \dfrac{\pi}{180}
\Rightarrow 60^\circ=\dfrac{\pi}3\)
Пример 2. Найти градусную меру угла \(\dfrac34 \pi\).
Т.к. \(\pi=180^\circ \Rightarrow \dfrac34 \pi=\dfrac34 \cdot
180^\circ=135^\circ\).
Обычно пишут, например, не \(\dfrac{\pi}4 \text{ рад}\), а просто \(\dfrac{\pi}4\) (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают. Таким образом, под записью “угол равен \(1\)” понимают, что “угол равен \(1\) радиану”, а не “угол равен \(1\) градусу”.
Т.к. \(\pi \thickapprox 3,14 \Rightarrow 180^\circ \thickapprox 3,14
\textbf{ рад} \Rightarrow 1 \textbf{ рад} \thickapprox 57^\circ\).
Такую приблизительную подстановку делать в задачах нельзя, но знание того, чему приближенно равен \(1\) радиан в градусах часто помогает при решении некоторых задач. Например, таким образом проще найти на окружности угол в \(5\) радиан: он примерно равен \(285^\circ\).
\(\blacktriangleright\) Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов \(0<\alpha< 90^\circ\) определены синус, косинус, тангенс и котангенс следующим образом:
если дан прямоугольный треугольник со сторонами \(a, b, c\) и углом \(\alpha\), то:

Т.к. на единичной окружности определены любые углы \(\alpha\in(-\infty;+\infty)\), то нужно определить синус, косинус, тангенс и котангенс для любого угла.
Рассмотрим единичную окружность и на ней угол \(\alpha\) и соответствующую ему точку \(P_{\alpha}\):
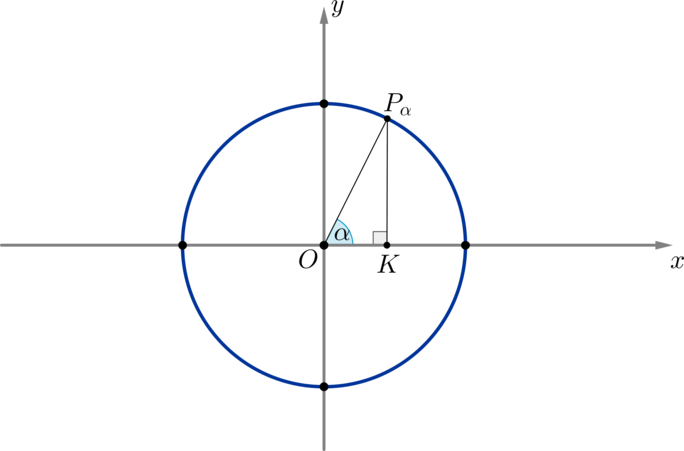
Опустим перпендикуляр \(P_{\alpha}K\) из точки \(P_{\alpha}\) на ось \(Ox\). Мы получим прямоугольный треугольник \(\triangle OP_{\alpha}K\), из которого имеем: \[\sin\alpha=\dfrac{P_{\alpha}K}{P_{\alpha}O} \qquad \cos \alpha=\dfrac{OK}{P_{\alpha}O}\] Заметим, что отрезок \(OK\) есть не что иное, как абсцисса \(x_{\alpha}\) точки \(P_{\alpha}\), а отрезок \(P_{\alpha}K\) — ордината \(y_{\alpha}\). Заметим также, что т.к. мы брали единичную окружность, то \(P_{\alpha}O=1\) — ее радиус.
Таким образом, \[\sin\alpha=y_{\alpha}, \qquad \cos \alpha=x_{\alpha}\]
Таким образом, если точка \(P_{\alpha}\) имела координаты \((x_{\alpha}\,;y_{\alpha})\), то через соответствующий ей угол ее координаты можно переписать как \((\cos\alpha\,;\sin\alpha)\).
Определение: 1. Синусом угла \(\alpha\) называется ордината точки \(P_{\alpha}\), соответствующей этому углу, на единичной окружности.
2. Косинусом угла \(\alpha\) называется абсцисса точки \(P_{\alpha}\), соответствующей этому углу, на единичной окружности.
Поэтому ось \(Oy\) называют осью синусов, ось \(Ox\) — осью косинусов.
\(\blacktriangleright\) Окружность можно разбить на \(4\) четверти, как показано на рисунке.
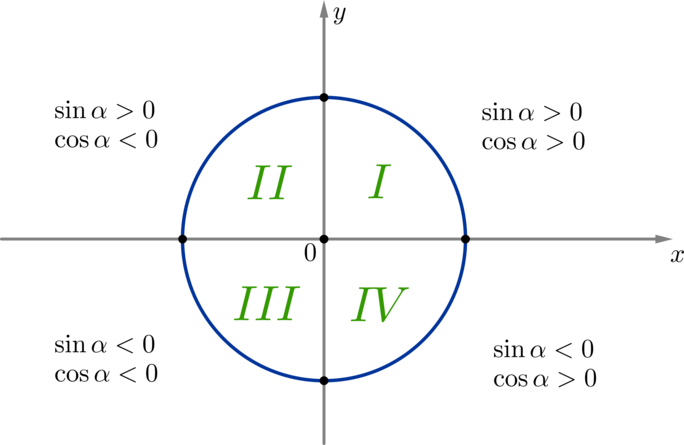
Т.к. в \(I\) четверти и абсциссы, и ординаты всех точек положительны, то косинусы и синусы всех углов из этой четверти также положительны.
Т.к. во \(II\) четверти ординаты всех точек положительны, а абсциссы — отрицательны, то косинусы всех углов из этой четверти — отрицательны, синусы — положительны.
Аналогично можно определить знак синуса и косинуса для оставшихся четвертей.
Пример 3. Так как, например, точки \(P_{\frac{\pi}{6}}\) и \(P_{-\frac{11\pi}6}\) совпадают, то их координаты равны, т.е. \(\sin\dfrac{\pi}6=\sin \left(-\dfrac{11\pi}6\right),\ \cos
\dfrac{\pi}6=\cos
\left(-\dfrac{11\pi}6\right)\).
Пример 4. Рассмотрим точки \(P_{\alpha}\) и \(P_{\pi-\alpha}\). Пусть для удобства \(0<\alpha<\dfrac{\pi}2\).
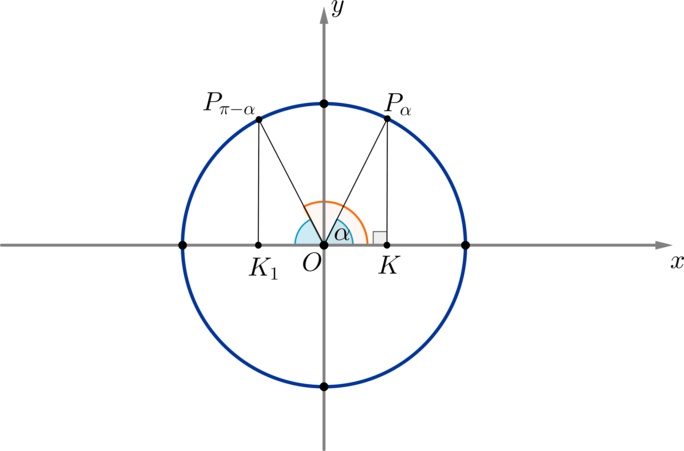
Проведем перпендикуляры на ось \(Ox\): \(OK\) и \(OK_1\). Треугольники \(OKP_{\alpha}\) и \(OK_1P_{\pi-\alpha}\) равны по гипотенузе и углу (\(\angle P_{\alpha}OK=\angle P_{\pi-\alpha}OK_1=\alpha\)).
Следовательно, \(OK=OK_1, KP_{\alpha}=K_1P_{\pi-\alpha}\).
Т.к. координаты точки \(P_{\alpha}=(OK;KP_{\alpha})=(\cos\alpha\,;\sin\alpha)\), а точки \(P_{\pi-\alpha}=(-OK_1;K_1P_{\pi-\alpha})=(\cos(\pi-\alpha)\,;\sin(\pi-\alpha))\), следовательно, \[\cos(\pi-\alpha)=-\cos\alpha, \qquad \sin(\pi-\alpha)=\sin\alpha\]
Таким образом доказываются и другие формулы, называемые формулами приведения: \[{\large{\begin{array}{l|r}
\hline \sin(\pi-\alpha)=\sin\alpha &
\cos(\pi-\alpha)=-\cos\alpha\\[2ex]
\sin(\pi+\alpha)=-\sin\alpha &
\cos(\pi+\alpha)=-\cos\alpha\\[2ex]
\sin(2\pi\pm\alpha)=\pm\sin\alpha & \cos
(2\pi\pm\alpha)=\cos\alpha\\[2ex]
\sin \left(\dfrac{\pi}2\pm\alpha\right)=\cos\alpha &
\cos\left(\dfrac{\pi}2\pm\alpha\right)=\pm\sin\alpha\\[2ex]
\hline
\end{array}}}\]
С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из \(I\) четверти.
Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
\[{\large{\begin{array}{|c|c|c|c|c|c|}
\hline &&&&&\\[-17pt]
& \quad 0 \quad (0^ \circ)& \quad \dfrac{\pi}6 \quad (30^\circ)
& \quad \dfrac{\pi}4
\quad (45^\circ) & \quad \dfrac{\pi}3 \quad (60^\circ)& \quad \dfrac{\pi}2 \quad
(90^\circ) \\
&&&&&\\[-17pt]
\hline \sin & 0 &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2&1\\[4pt]
\hline \cos &1&\frac{\sqrt3}2&\frac{\sqrt2}2&\frac12&0\\[4pt]
\hline \mathrm{tg} &0 &\frac{\sqrt3}3&1&\sqrt3&\infty\\[4pt]
\hline \mathrm{ctg} &\infty &\sqrt3&1&\frac{\sqrt3}3&0\\[4pt]
\hline
\end{array}}}\]
Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”.
Пример 5. Найдите \(\sin{\dfrac{3\pi}4}\).
Преобразуем угол: \(\dfrac{3\pi}4=\dfrac{4\pi-\pi}{4}=\pi-\dfrac{\pi}4\)
Таким образом, \(\sin{\dfrac{3\pi}4}=\sin\left(\pi-\dfrac{\pi}4\right)=\sin\dfrac{\pi}4=\dfrac{\sqrt2}2\).
\(\blacktriangleright\) Для упрощения запоминания и использования формул приведения можно следовать следующему правилу.
Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm
\alpha\), где \(n\in\mathbb{N}\), то \[\sin(n\cdot \pi\pm
\alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\). \[\cos(n\cdot \pi\pm
\alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\).
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол \(\alpha\) находится в \(I\) четверти.
Случай 2. Если угол можно представить в виде \(n\cdot
\pi+\dfrac{\pi}2\pm\alpha\), где \(n\in\mathbb{N}\), то \[\sin(n\cdot \pi+\dfrac{\pi}2\pm
\alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\). \[\cos(n\cdot \pi+\dfrac{\pi}2\pm
\alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\).
Знак определяется таким же образом, как и в случае \(1\).
Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Пример 6. Найти \(\sin \dfrac{13\pi}{3}\).
Преобразуем угол: \(\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3\), следовательно, \(\sin \dfrac{13\pi}{3}=\sin
\left(4\pi+\dfrac{\pi}3\right)=\sin\dfrac{\pi}3=\dfrac{\sqrt3}2\)
Пример 7. Найти \(\cos \dfrac{17\pi}{6}\).
Преобразуем угол: \(\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6\), следовательно, \(\cos \dfrac{17\pi}{6}=\cos
\left(3\pi-\dfrac{\pi}6\right)=-\cos\dfrac{\pi}6=-\dfrac{\sqrt3}2\)
\(\blacktriangleright\) Область значений синуса и косинуса.
Т.к. координаты \(x_{\alpha}\) и \(y_{\alpha}\) любой точки \(P_{\alpha}\) на единичной окружности находятся в пределах от \(-1\) до \(1\), а \(\cos\alpha\) и \(\sin\alpha\) — абсцисса и ордината соответственно этой точки, то \[{\large{-1\leq \cos\alpha\leq 1 ,\qquad -1\leq\sin\alpha\leq 1}}\] 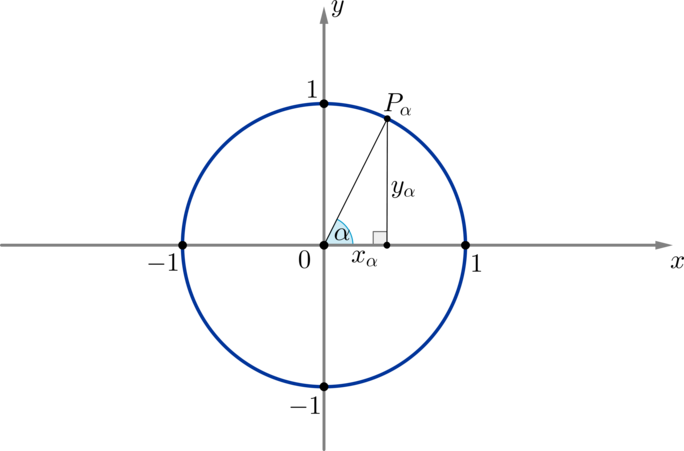
Из прямоугольного треугольника по теореме Пифагора имеем: \(x^2_{\alpha}+y^2_{\alpha}=1^2\)
Т.к. \(x_{\alpha}=\cos\alpha,\ y_{\alpha}=\sin\alpha \Rightarrow\) \[{\large{\sin^2\alpha+\cos^2\alpha=1}} - \textbf{основное тригонометрическое тождество (ОТТ)}\]
\(\blacktriangleright\) Тангенс и котангенс.
Т.к. \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}, \cos\alpha\ne 0\)
\(\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}, \sin\alpha\ne 0\), то:
1) \({\large{\mathrm{tg}\,\alpha\cdot \mathrm{ctg}\,\alpha=1, \cos\alpha\ne 0, \sin\alpha \ne 0}}\)
2) тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны в \(II\) и \(IV\) четвертях.
3) область значений тангенса и котангенса — все вещественные числа, т.е. \(\mathrm{tg}\,\alpha\in\mathbb{R}, \
\mathrm{ctg}\,\alpha\in\mathbb{R}\)
4) для тангенса и котангенса также определены формулы приведения.
Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm
\alpha\), где \(n\in\mathbb{N}\), то \[\mathrm{tg}\,(n\cdot \pi\pm
\alpha)=\bigodot \mathrm{tg}\,\alpha\] где на месте \(\bigodot\) стоит знак тангенса угла \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\)). \[\mathrm{ctg}\,(n\cdot \pi\pm
\alpha)=\bigodot \mathrm{ctg}\,\alpha\] где на месте \(\bigodot\) стоит знак котангенса угла \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\)).
Случай 2. Если угол можно представить в виде \(n\cdot
\pi+\dfrac{\pi}2\pm\alpha\), где \(n\in\mathbb{N}\), то \[\mathrm{tg}\,(n\cdot \pi+\dfrac{\pi}2\pm
\alpha)=\bigodot \mathrm{ctg}\,\alpha\] где на месте \(\bigodot\) стоит знак тангенса угла \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\)). \[\mathrm{ctg}\,(n\cdot \pi+\dfrac{\pi}2\pm
\alpha)=\bigodot \mathrm{tg}\,\alpha\] где на месте \(\bigodot\) стоит знак котангенса угла \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\)).
5) ось тангенсов проходит через точку \((1;0)\) параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов;
ось котангенсов — через точку \((0;1)\) параллельно оси косинусов, причем положительное направление оси котангенсов совпадает с положительным направлением оси косинусов.
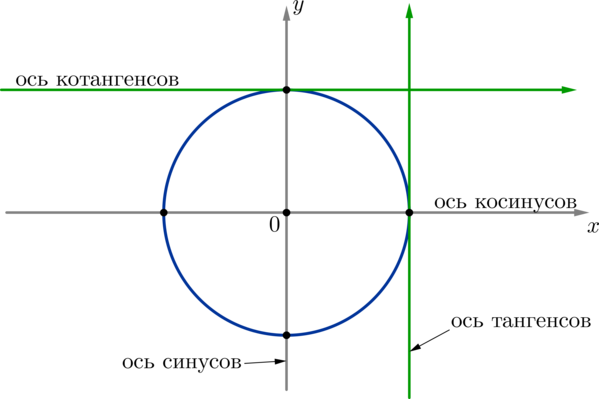
Доказательство этого факта приведем на примере оси тангенсов.
\(\triangle OP_{\alpha}K \sim \triangle AOB \Rightarrow
\dfrac{P_{\alpha}K}{OK}=\dfrac{BA}{OB} \Rightarrow
\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{BA}1 \Rightarrow
BA=\mathrm{tg}\,\alpha\).
Таким образом, если точку \(P_{\alpha}\) соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно \(\mathrm{tg}\,\alpha\).
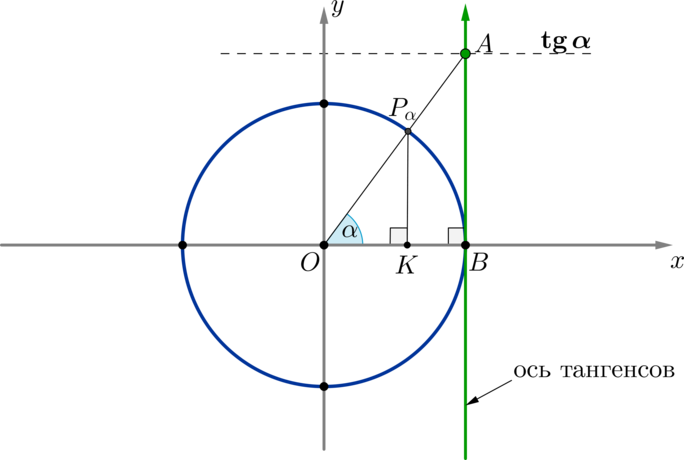
6) из основного тригонометрического тождества вытекают следующие формулы: \[1+\mathrm{tg}\,^2\alpha=\dfrac1{\cos^2\alpha},\cos\alpha\ne 0 \qquad \qquad 1+\mathrm{ctg}\,^2\alpha=\dfrac1{\sin^2\alpha}, \sin\alpha\ne 0\] Первую формулу получают делением правой и левой частей ОТТ на \(\cos^2\alpha\), вторую — делением на \(\sin^2\alpha\).
Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это \(\alpha=\dfrac{\pi}2+\pi n, n\in\mathbb{Z}\));
котангенс не определен в углах, где синус равен нулю (это \(\alpha=\pi+\pi n, n\in\mathbb{Z}\)).
\(\blacktriangleright\) Четность косинуса и нечетность синуса, тангенса, котангенса.
Напомним, что функция \(f(x)\) называется четной, если \(f(-x)=f(x)\).
Функция называется нечетной, если \(f(-x)=-f(x)\).
По окружности видно, что косинус угла \(\alpha\) равен косинусу угла \(-\alpha\) при любых значениях \(\alpha\):
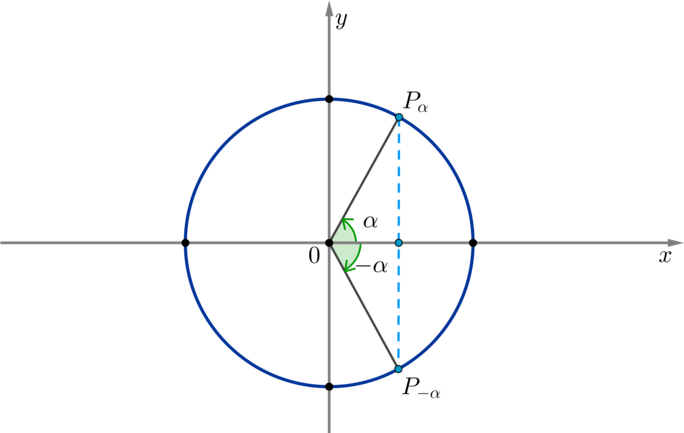
Таким образом, косинус — четная функция, значит, верна формула \[{\Large{\cos(-x)=\cos x}}\]
По окружности видно, что синус угла \(\alpha\) противоположен синусу угла \(-\alpha\) при любых значениях \(\alpha\):
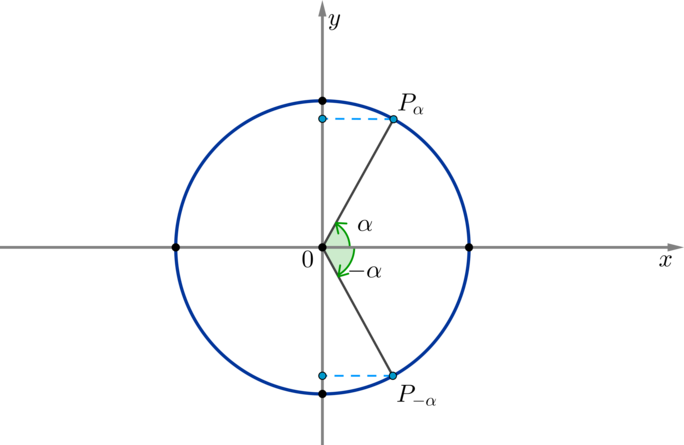
Таким образом, синус — нечетная функция, значит, верна формула \[{\Large{\sin(-x)=-\sin x}}\]
Тангенс и котангенс также нечетные функции: \[{\Large{\mathrm{tg}\,(-x)=-\mathrm{tg}\,x}}\] \[{\Large{\mathrm{ctg}\,(-x)=-\mathrm{ctg}\,x}}\]
Т.к. \(\mathrm{tg}\,(-x)=\dfrac{\sin (-x)}{\cos(-x)}=\dfrac{-\sin
x}{\cos x}=-\mathrm{tg}\,x \qquad \mathrm{ctg}\,(-x)=\dfrac{\cos(-x)}{\sin(-x)}=-\mathrm{ctg}\,x\))
















