Определение
Многогранником будем называть замкнутую поверхность, составленную из многоугольников и ограничивающую некоторую часть пространства.
Отрезки, являющиеся сторонами этих многоугольников, называются ребрами многогранника, а сами многоугольники – гранями. Вершины многоугольников называются вершинами многогранника.
Будем рассматривать только выпуклые многогранники (это такой многогранник, который находится по одну сторону от каждой плоскости, содержащей его грань).
Многоугольники, из которых составлен многогранник, образуют его поверхность. Часть пространства, которую ограничивает данный многогранник, называется его внутренностью.
Определение: призма
Рассмотрим два равных многоугольника \(A_1A_2A_3...A_n\) и \(B_1B_2B_3...B_n\), находящихся в параллельных плоскостях так, что отрезки \(A_1B_1, \ A_2B_2, ..., A_nB_n\) параллельны. Многогранник, образованный многоугольниками \(A_1A_2A_3...A_n\) и \(B_1B_2B_3...B_n\), а также параллелограммами \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, ...\), называется (\(n\)-угольной) призмой.
Многоугольники \(A_1A_2A_3...A_n\) и \(B_1B_2B_3...B_n\) называются основаниями призмы, параллелограммы \(A_1B_1B_2A_2, \ A_2B_2B_3A_3,
...\) – боковыми гранями, отрезки \(A_1B_1, \ A_2B_2, \ ..., A_nB_n\) – боковыми ребрами.
Таким образом, боковые ребра призмы параллельны и равны между собой.
Рассмотрим пример — призма \(A_1A_2A_3A_4A_5B_1B_2B_3B_4B_5\), в основании которой лежит выпуклый пятиугольник.
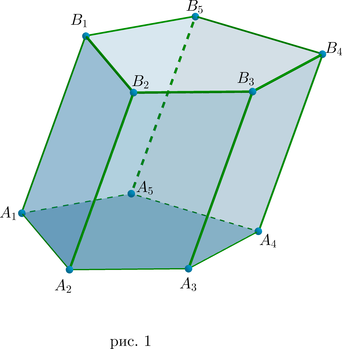
Высота призмы – это перпендикуляр, опущенный из любой точки одного основания к плоскости другого основания.
Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (рис. 1), в противном случае – прямой. У прямой призмы боковые ребра являются высотами, а боковые грани – равными прямоугольниками.
Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной.
Определение: понятие объема
Единица измерения объема – единичный куб (куб размерами \(1\times1\times1\) ед\(^3\), где ед — некоторая единица измерения).
Можно сказать, что объем многогранника – это величина пространства, которую ограничивает этот многогранник. Иначе: это величина, числовое значение которой показывает, сколько раз единичный куб и его части вмещаются в данный многогранник.
Объем имеет те же свойства, что и площадь:
1. Объемы равных фигур равны.
2. Если многогранник составлен из нескольких непересекающихся многогранников, то его объем равен сумме объемов этих многогранников.
3. Объем – величина неотрицательная.
4. Объем измеряется в см\(^3\) (кубические сантиметры), м\(^3\) (кубические метры) и т.д.
Теорема
1. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
Площадь боковой поверхности — сумма площадей боковых граней призмы.
2. Объем призмы равен произведению площади основания на высоту призмы: \[V_{\text{призмы}}=S_{\text{осн}}\cdot h\]
Определение: параллелепипед
Параллелепипед – это призма, в основании которой лежит параллелограмм.
Все грани параллелепипеда (их \(6\): \(4\) боковые грани и \(2\) основания) представляют собой параллелограммы, причем противоположные грани (параллельные друг другу) представляют собой равные параллелограммы (рис. 2).
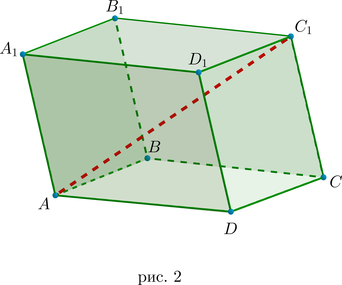
Диагональ параллелепипеда – это отрезок, соединяющий две вершины параллелепипеда, не лежащие в одной грани (их \(8\): \(AC_1, \
A_1C, \ BD_1, \ B_1D\) и т.д.).
Прямоугольный параллелепипед — это прямой параллелепипед, в основании которого лежит прямоугольник.
Т.к. это прямой параллелепипед, то боковые грани представляют собой прямоугольники. Значит, вообще все грани прямоугольного параллелепипеда – прямоугольники.
Все диагонали прямоугольного параллелепипеда равны (это следует из равенства треугольников \(\triangle ACC_1=\triangle AA_1C=\triangle
BDD_1=\triangle BB_1D\) и т.д.).
Замечание
Таким образом, параллелепипед обладает всеми свойствами призмы.
Теорема
Площадь боковой поверхности прямоугольного параллелепипеда равна \[S_{\text{боков.пов-ти прямоуг. пар-да}}=2(a+b)c\]
Площадь полной поверхности прямоугольного параллелепипеда равна \[S_{\text{полн.пов-ти прямоуг. пар-да}}=2(ab+ac+bc)\]
Теорема
Объем прямоугольного параллелепипеда равен произведению трех его ребер, выходящих из одной вершины (три измерения прямоугольного параллелепипеда): \[V_{\text{прямоуг.пар-да}}=abc\]
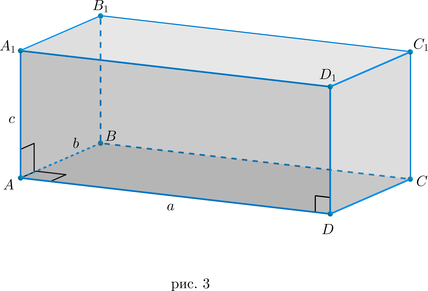
Доказательство
Т.к. у прямоугольного параллелепипеда боковые ребра перпендикулярны основанию, то они являются и его высотами, то есть \(h=AA_1=c\) Т.к. в основании лежит прямоугольник, то \(S_{\text{осн}}=AB\cdot AD=ab\). Отсюда и следует данная формула.
Теорема
Диагональ \(d\) прямоугольного параллелепипеда ищется по формуле (где \(a,b,c\) — измерения параллелепипеда) \[d^2=a^2+b^2+c^2\]
Доказательство
Рассмотрим рис. 3. Т.к. в основании лежит прямоугольник, то \(\triangle ABD\) – прямоугольный, следовательно, по теореме Пифагора \(BD^2=AB^2+AD^2=a^2+b^2\).
Т.к. все боковые ребра перпендикулярны основаниям, то \(BB_1\perp
(ABC) \Rightarrow BB_1\) перпендикулярно любой прямой в этой плоскости, т.е. \(BB_1\perp BD\). Значит, \(\triangle BB_1D\) – прямоугольный. Тогда по теореме Пифагора \(B_1D=BB_1^2+BD^2=a^2+b^2+c^2\), чтд.
Определение: куб
Куб — это прямоугольный параллелепипед, все грани которого – равные квадраты.
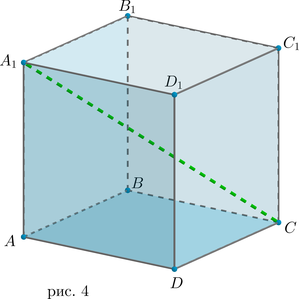
Таким образом, три измерения равны между собой: \(a=b=c\). Значит, верны следующие
Теоремы
1. Объем куба с ребром \(a\) равен \(V_{\text{куба}}=a^3\).
2. Диагональ куба ищется по формуле \(d=a\sqrt3\).
3. Площадь полной поверхности куба \(S_{\text{полн.пов-ти
куба}}=6a^2\).







