Рациональное неравенство — это неравенство, которое можно свести к виду \[\Large{\dfrac{P(x)}{Q(x)}\lor 0}\]где \(P(x),\
Q(x)\) — многочлены.
(\(\lor\) — один из знаков \(\geqslant,
\ \leqslant, \ >, \ <\))
Например, следующие неравенства являются рациональными: \[\dfrac1{x+1}>0,\qquad x+2+\dfrac{x-1}{x+3}<1,\qquad x^2+x-2\leqslant 0\]
\[{\Large{\text{Линейные неравенства}}}\] Линейные неравенства – это неравенства вида \[ax+b \lor 0, \qquad
\lor - \text{ один из знаков } \geqslant, \ \leqslant, \ >, \
<;\quad a,b - \text{ числа,}\]или сводящиеся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).
Общее правило решения линейных неравенств:
1) Для того, чтобы решить данное неравенство, необходимо привести его к виду \(ax\lor -b\), то есть перенести число \(b\) в правую часть.
2) Если коэффициент \(a\) перед \(x\) – положительный, то неравенство равносильно \(x\lor -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства не меняется.
3) Если коэффициент \(a\) перед \(x\) – отрицательный, то неравенство равносильно \(x\land -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства меняется на противоположный.
4) Если \(a=0\), то неравенство равносильно \(0\lor -b\), что либо верно при всех значениях переменной \(x\) (например, если это \(0>-1\)), либо неверно ни при каких значениях \(x\) (например, если это \(0\leqslant -3\)).
То есть ответом будут либо \(x\in\mathbb{R}\), либо \(x\in
\varnothing\).
Замечание
Заметим, что знаку \(\leqslant\) противоположен знак \(\geqslant\), а знаку \(<\) – знак \(>\). И наоборот.
Пример 1
Решить неравенство \(5-3x>-1\).
Решение. I способ
Сделаем цепочку преобразований:
\[5-3x>-1 \ \Rightarrow \ -3x>-1-5 \ \Rightarrow \ -3x>-6 \
\Rightarrow \ x<\dfrac 63 \ \Rightarrow \ x<2\] Таким образом, ответом будет \(x\in(-\infty;2)\).
Заметим, что т.к. мы делили неравенство на \(-3\), то знак неравенства поменялся.
Решение. II способ
Можно перенести слагаемое \(-3x\) в правую часть, а \(-1\) – в левую:
\[5-3x>-1 \ \Rightarrow \ 5+1>3x \ \Rightarrow \ 3x<6 \ \Rightarrow \ x<2\]
Пример 2
Решить неравенство \((1-\sqrt2)x+2\leqslant 0\).
Решение
Заметим, что перед \(x\) находится отрицательный коэффициент. Поэтому:
\[(1-\sqrt2)x\leqslant -2 \Rightarrow x\geqslant -\dfrac 2{1-\sqrt2}\] Преобразуем число \(-\dfrac 2{1-\sqrt2}\): домножим числитель и знаменатель дроби на сопряженное к \(1-\sqrt2\), то есть на \(1+\sqrt2\), чтобы избавиться от иррациональности в знаменателе:
\[-\dfrac 2{1-\sqrt2}=-\dfrac{2(1+\sqrt2)}{(1-\sqrt2)(1+\sqrt2)}=
-\dfrac{2(1+\sqrt2)}{1-2}=2(1+\sqrt2)\]
Таким образом, ответ \(x\in [2+2\sqrt2;+\infty)\).
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.
\[{\Large{\text{Метод интервалов}}}\]
Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида
\[(**)\qquad \dfrac{P(x)}{Q(x)}\geqslant 0 \qquad (\text{на месте }\geqslant
\text{может стоять любой из} \leqslant, \ <, \ >)\]
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.
Существует два способа решения таких неравенств:
1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности: \[{\large{\left[\begin{gathered}
\begin{aligned}
&\begin{cases} P(x)\geqslant 0\\ Q(x)>0 \end{cases}\\
&\begin{cases} P(x)\leqslant 0\\ Q(x)<0 \end{cases}
\end{aligned}
\end{gathered}
\right.}}\]
Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — \(0\).
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.
2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!
1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался \(0\), и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены \(P(x), \ Q(x)\), на множители.
Например, неравенство \(\dfrac1{x+1}<1\) нужно переписать в виде \(\dfrac1{x+1}-1<0\), затем привести к общему
знаменателю \(\dfrac1{x+1}-\dfrac{x+1}{x+1}<0\), затем записать в виде одной дроби левую часть: \(\dfrac{1-(x+1)}{x+1}<0\) и
привести подобные слагаемые: \(\dfrac{-x}{x+1}<0\).
Итак, пусть после разложения на множители неравенство приняло вид \[\dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2}
\geqslant0\]
Заметим, что любой многочлен можно (а в нашем способе НУЖНО) разложить до произведения только линейных скобок (\(ax+b\)) и квадратичных скобок с отрицательным дискриминантом \((ax^2+bx+c), \ D<0\).
2 ШАГ. Рассмотрим скобки, в которых остался квадратичный трехчлен с \(D<0\).
\(\bullet\) Если при \(x^2\) находится положительный коэффициент \(a>0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) положительно (не может быть равно нулю!). Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x^2+3x+5)\)). Причем заметим, что т.к. мы делим на положительное выражение, то знак неравенства не меняется!
\(\bullet\) Если при \(x^2\) находится отрицательный коэффициент \(a<0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) отрицательно. Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x-x^2-3)\)). Причем заметим, что т.к. мы делим на отрицательное выражение, то знак неравенства должен измениться на противоположный!
Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с \(a>0\) знак неравенства остается прежним, а вот при вычеркивании скобок с \(a<0\) знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.
Таким образом, неравенство примет вид \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2}
\leqslant 0\]
3 ШАГ. Рассмотрим линейные скобки \((ax+b)\).
Назовем скобку хорошей, если при \(x\) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при \(x\) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).
Для того, чтобы в одной плохой скобке поменять все знаки на противоположные, необходимо домножить правую и левую части неравенства на \(-1\). Таким образом, после одного такого действия знак неравенства сменится на противоположный. Значит, если плохих скобок четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.
Заметим, что выражение \((ax+b)^n\) — это не что иное, как произведение \(n\) скобок \((ax+b)\).
В нашем неравенстве среди плохих одна скобка \((3-x)\) и две скобки \((2-3x)\) (т.к. \((2-3x)^2=(2-3x)(2-3x)\)), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2}
\geqslant0\quad (***)\]
Заметим, что множитель \(x^2\) — это скобка \((x-0)^2\), или, что то же самое, \((x-0)(x-0)\) – произведение двух одинаковых линейных скобок.
4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.
Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.
А нам как раз нужно найти те значения \(x\), при которых функция \(\geqslant 0\). Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа (\(\mathbb{R}\)), кроме нулей знаменателя. Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть \(\geqslant \) или \(\leqslant \)) или выколотые (если знак неравенства строгий, то есть \(>\) или \(<\)).
Заметим, что если мы отметили \(n\) точек, то числовая прямая разобьется на \(n+1\) промежутков.
Расставим знак на каждом промежутке \(\color{red}{{\Large{\text{справа налево}}}}\). Будем ставить “\(+\)”, если функция на этом промежутке принимает положительные значения, и “\(-\)” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность. Какую – вы узнаете дальше.
Но в любом случае способ расстановки знаков путем подстановки чисел остается в нашем арсенале.
Т.к. все скобки – хорошие, то первый знак всегда будет “\(+\,\)” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень \(x=3\)), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.
Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки \(-1, \ 0, \ \dfrac23\) (например, точка \(-1\) входит в четное количество скобок: одна в числителе \((x+1)\) и три в знаменателе \((x+1)^3\)).
Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки \(3\) и \(1\)).

Объясним, почему так происходит. Каждая линейная скобка в нечетной степени \((x-a)^{2n+1}\) имеет ровно один корень \(x=a\), причем, т.к. мы сделали ее хорошей, то для всех \(x>a\) она будет положительной, для всех \(x<a\) она будет отрицательной (а для \(x=a\), естественно, равной нулю). Значит, когда \(x\in (1;3)\), то все скобки, кроме \((x-3)\), будут оставаться положительными, и лишь эта скобка \((x-3)\) станет отрицательной. Значит, их произведение также станет отрицательным. Аналогично при переходе через точку \(x=1\).
Каждая линейная скобка в четной степени \((x-b)^{2n}\) также имеет ровно один корень \(x=b\), но т.к. она в четной степени, то при всех \(x\ne b\) она всегда будет положительной! И только при \(x=b\) она будет равна нулю. Именно поэтому при переходе через точку \(x=\dfrac23\), т.е. на \(x\in(0;\frac23)\), скобка \((3x-2)^2\) не сменит свой знак на отрицательный, поэтому вся левая часть останется по знаку такой же, как и была на \((\frac23;1)\) (т.е. положительной). Аналогично при переходе через точки \(0, -1\).
5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного \((***)\) неравенства \(\geqslant 0\) (нестрогий), то в ответ пойдут промежутки со знаком “\(+\,\)” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): \[x\in \Big(-\infty;-1\Big)\cup \left(-1;\dfrac23\right)\cup
\left(\dfrac23;1\right]\cup\Big(3;+\infty\Big)\]Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “\((\)” или “\()\)”, если входит в ответ – то в квадратной скобке “\([\)” или “\(]\)”. Бесконечности всегда пишутся в круглых скобках.
\[{\Large{\text{Квадратичные неравенства}}}\]
Квадратичным неравенством называется любое неравенство вида \[ax^2+bx+c \lor 0, \quad a\ne 0,\]
или сводящееся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).
Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.
Замечание
Вспомним, как преобразуется квадратичный трехчлен \(ax^2+bx+c\) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение \(ax^2+bx+c=0\)
\(\bullet\) имеет два корня \(x_1\) и \(x_2\) (дискриминант \(D>0\)), то \(ax^2+bx+c=a(x-x_1)(x-x_2)\).
\(\bullet\) имеет один корень \(x_1\) (\(D=0\)), то \(ax^2+bx+c=a(x-x_1)^2\).
\(\bullet\) не имеет корней (\(D<0\)), то квадратный трехчлен \(ax^2+bc+c\) никогда не может быть равен нулю и не разлагается на линейные множители.
Шаг 1. Рассмотрим функцию \(f(x)=ax^2+bx+c\). Графиком такой функции является парабола.
Для того, чтобы решить квадратичное неравенство, изобразим схематично параболу: то есть определим, куда направлены ее ветви и в каких точках она пересекает ось \(Ox\).
Если \(a>0\), то ветви направлены вверх, если \(a<0\), то ветви направлены вниз. Корни уравнения \(ax^2+bx+c=0 \ (*)\) и есть абсциссы точек, в которых парабола пересекает ось \(Ox\).
Шаг 2. Таким образом, наша парабола будет одного из 6 видов: 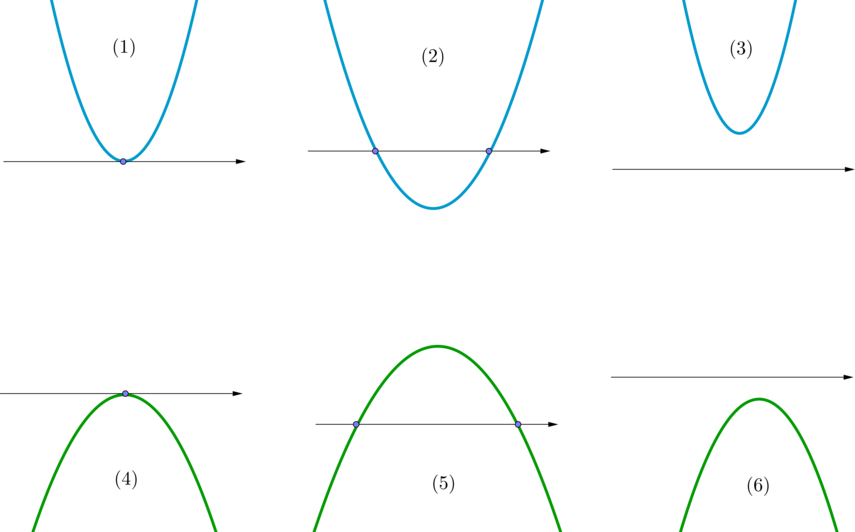
\((1)\) и \((4)\) — когда уравнение \((*)\) имеет один корень;
\((2)\) и \((5)\) — когда уравнение \((*)\) имеет два корня;
\((3)\) и \((6)\) — когда уравнение \((*)\) не имеет корней.
Часть параболы, находящая выше оси \(Ox\), отвечает за \(f(x)>0\);
часть параболы, находящаяся ниже оси \(Ox\), отвечает за \(f(x)<0\);
точки, в которых парабола пересекает ось \(Ox\), отвечают за \(f(x)=0\).
Пример 1.
Решить неравенство \(x^2+3x+2\geqslant 0\).
Решение
Решим уравнение \(x^2+3x+2=0 \Leftrightarrow x_1=-2, x_2=-1\). Таким образом, неравенство можно переписать в виде: \((x+1)(x+2)\geqslant
0\). Ветви параболы направлены вверх, следовательно, схематично она выглядит как \((2)\). Т.к. знак неравенства \(\geqslant\), то решением неравенства будут те значения \(x\), для которых график находится выше оси \(Ox\), а именно \(x\in (-\infty;-2]\cup[-1;+\infty)\).
Заметим, что точки \(-2, -1\) входят в ответ, потому что знак “больше или равно”.
Пример 2.
Решить неравенство \(11x-3x^2-6>0\)
Решение
Решим уравнение \(11x-3x^2-6=0 \quad\Leftrightarrow\quad
x_1=\dfrac23, x_2=3\). Таким образом, неравенство можно переписать в виде: \(-3(x-3)(x-\frac23)>0\).
1 способ. Ветви параболы направлены вниз, следовательно, схематично она выглядит как \((5)\). Т.к. знак неравенства \(>\), то решением неравенства будут \(x\in \left(\dfrac23;3\right)\).
2 способ. Домножим правую и левую части неравенства на \(-1\), получим \(3(x-3)(x-\frac23)<0\) (заметим, что знак сменился на противоположный). У новой параболы \(\Big(f(x)=3(x-3)(x-\frac23)\Big)\) ветви направлены вверх, следовательно, схематично она выглядит как \((2)\). Но знак неравенства уже \(<\). Решением нового неравенства, естественно, будут те же \(x\in \left(\dfrac23;3\right)\).
Таким образом, если в квадратичном неравенстве отрицательный знак при \(x^2\), то можно сначала домножить неравенство на \(-1\) (и не забыть поменять знак неравенства), чтобы ветви параболы всегда были направлены вверх.
Пример 3.
Решить неравенство \(x^2+4x+4 \geqslant 0\).
Решение
Вспомнив формулу сокращенного умножения, получаем \((x+2)^2\geqslant
0\) (это быстрее, чем находить корни через дискриминант :)). Таким образом, парабола пересекает ось \(Ox\) в единственной точке \(x_1=-2\) и выглядит как \((1)\). А т.к. нам нужны те \(x\), для которых график находится не ниже оси \(Ox\), то решением неравенства будут \(x\in
\mathbb{R}\), то есть выражение \((x+2)^2\) всегда больше или равно \(0\).





