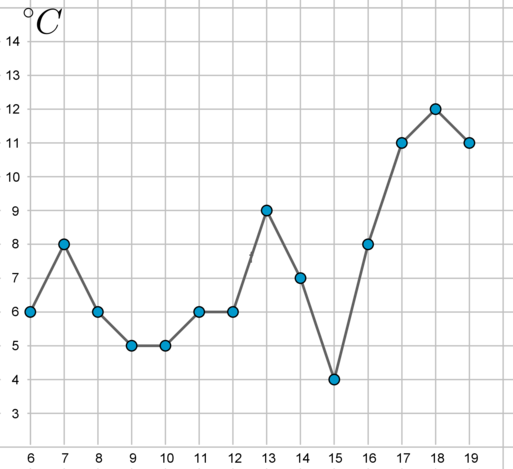
а) Так как \(1+6=7\), то первая цифра искомого числа \(1\), вторая \(6\): \(16...\)
Так как \(6+8=14\), то третья цифра – это \(8\): \(168...\)
Аналогично четвертая, последняя, цифра числа – это \(9\).
Таким образом, число \(1689\).
б) Предположим, что такое число существует. Начнем так же, как в пункте а), определять цифры этого числа слева направо. Очевидно, что первые две цифры – это \(3\) и \(7\), то есть число \(37...\)
Третья цифра не может быть \(1\), так как \(7+1\ne 6\) и \(7+1\ne 61\). Также она не может быть равна \(0\), \(9\) или \(0\), так как в этом случае сумма двух цифр уже должна быть равна трех-, четырех- или пятизначному числу.
Следовательно, ответ: нет.
в) Пусть дано трехзначное число \(\overline{abc}\). Тогда из него получится число \(N=\overline{a\,(a+b)\,b\,(b+c)\,c}\).
Заметим, что при \(a+b\geqslant 10\) и \(b+c\geqslant 10\) данное число будет семизначным, а во всех остальных случаях — шести- или пятизначным. Таким образом, так как мы ищем наибольшее возможное число, то найдем его среди семизначных чисел.
Пусть \(a+b=10+x, b+c=10+y\), где \(0\leqslant x,y\leqslant 8\).
Тогда число имеет вид: \(N=\overline{a1xb1yc}\).
По признаку делимости число делится на \(11\) тогда и только тогда, когда сумма его цифр, стоящих на нечетных местах, минус сумма цифр, стоящих на четных местах, кратна \(11\). То есть: \[(a+x+1+c)-(1+b+y):11\] Так как \(x=a+b-10\), \(y=b+c-10\), то получаем: \[(a+a+b-10+1+c)-(1+b+b+c-10):11\quad\Rightarrow\quad 2a-b:11\] Для того, чтобы число \(N\) было наибольшим, его первая цифра должна быть наибольшей. Следовательно, если \(a=9\), то \(b=7\) (чтобы \(2a-b:11\)). Заметим, что \(c\) может быть любым. Следовательно, возьмем максимальное \(c=9\).
Таким образом, наибольшее число получится из числа \(979\) и равно \(N=9167169\).
Ответ:
а) 1689
б) нет
в) 9167169