Если выпускник планирует сдавать ЕГЭ по математике базового уровня и при этом стремится получить конкурентные баллы, ему непременно следует научиться решать задачи, в которых требуется найти высоту треугольника. Подобные планиметрические задания из года в год встречаются в аттестационном испытании. Это означает, что справляться с задачами ЕГЭ, в которых искомой величиной является высота треугольника, должны школьники с любым уровнем подготовки.
Полезная информация
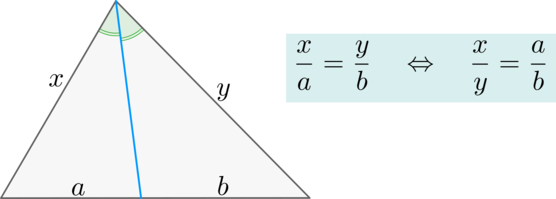
Задачи ЕГЭ, требующие найти угол между высотой и медианой или другую величину треугольника, зачастую можно решить, вспомнив основные понятия из базового школьного курса. При этом рекомендуется следовать определенному алгоритму. Вначале сделайте чертеж. Затем нанесите на него все известные данные согласно условию. После этого стоит определить все геометрические понятия (биссектриса, медиана треугольника и т. д.), которые известны и которые необходимо найти в задании ЕГЭ. Выполнив это, вспомните относящиеся к ним теоремы и отразите на чертеже все соотношения между элементами, которые из них следуют логически. Приведем пример. Если в задаче ЕГЭ встречается понятие «биссектриса угла треугольника», стоит вспомнить его определение и основные свойства, после чего найти и отразить на сделанном чертеже равные или пропорциональные отрезки и углы.
Как подготовиться к экзамену?
Задания в ЕГЭ на нахождение угла между биссектрисами треугольника, а также на вычисление отношения подобных треугольников вызывают у вас затруднения? Образовательный портал «Школково» поможет вам в решении этой проблемы. С нами вы сможете повторить материал по темам, которые являются для вас сложными. Наши специалисты собрали и изложили всю теоретическую информацию в максимально доступной и понятной форме.
Для каждого задания на портале вы найдете правильный ответ и описание алгоритма решения. Практиковаться можно как с простыми упражнениями, так и с более сложными. Тренироваться в решении задач на нахождение угла между биссектрисой и медианой треугольника, которые встречаются в ЕГЭ, выпускники могут в режиме онлайн, находясь в любом регионе России. Справившись в заданием, учащиеся имеют возможность сохранить его в разделе «Избранное», а затем при необходимости обсудить его с преподавателем в школе или репетитором.