Тренировочные варианты «Школково». Основная волна. Реальные варианты ЕГЭ 2015

Количество полных этажей, которые расположены ниже Мишиного, есть округлённый в меньшую сторону результат деления \(29\) на \(5\), следовательно, \(5\) этажей ниже, чем Мишин, тогда Миша живёт на \(6\) этаже.

Ответ: 6

Температура не превышала \(3\) градуса Цельсия \(1\), \(2\), \(3\), \(4\) и \(11\) марта, то есть \(5\) дней.

Ответ: 5

Наиболее дешёвый способ: снарядить 3 машины перевозчика “Мощный” на \(1000\ км\) (то есть по 10 раз) и ещё 2 машины перевозчика “Дешёвый” на \(1000\ км\), что обойдётся в \(3\cdot 4500\cdot 10 + 2\cdot 2000\cdot 10 = 175\,000\ руб\).

Ответ:

175000

Данный треугольник можно разрезать на два прямоугольных треугольника, как показано на рисунке. Площади полученных при этом треугольников будут равны \(0,5\cdot 4\cdot 6 = 12\) и \(0,5\cdot 6\cdot 6 = 18\), следовательно, площадь исходного треугольника равна \(12 + 18 = 30\).

Ответ: 30

Искомая вероятность есть отношение количества спортсменов из Дании к общему количеству спортсменов и равна \[\dfrac{8}{40} = 0,2\,.\]

Ответ: 0,2

Сделаем преобразования:

\[(3x + 4)^2 = (8 + 3x)^2\quad\Leftrightarrow\quad 9x^2 + 24x + 16 = 9x^2 + 48x + 64\quad\Leftrightarrow\quad x = -2\,.\]

Ответ: -2

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, то \(\angle NPK = 88^\circ : 2 = 44^\circ\).

\(\angle NPK\) – внешний угол треугольника \(NMP\), тогда \(\angle NPK = \angle NMK + \angle MNP\), откуда \[\angle MNP = 44^\circ - 35^\circ = 9^\circ\,.\]

Ответ: 9

В точке максимума производная равна \(0\), причём в некоторой окрестности точки максимума слева от неё производная должна быть положительна, а справа от неё – отрицательна. Таким образом, функция \(f(x)\) имеет единственную точку максимума на указанном отрезке (\(x = 15\)).

Ответ: 1

В правильной пирамиде проекция \(O\) вершины \(M\) на плоскость основания есть центр описанной около основания окружности.

В правильном шестиугольнике расстояние от центра до вершины равно стороне, следовательно, \(AO = 5\). Заметим, что \(\triangle MOA\) — прямоугольный, т.к. \(MO\) перпендикулярно плоскости основания. По теореме Пифагора \[MO^2 = MA^2 - AO^2\qquad\Rightarrow\qquad MO = \sqrt{13^2 - 5^2} = 12\,.\]

Ответ: 12

Используя формулу косинуса двойного угла \(\cos 2x = 1 - 2\sin^2 x\), получаем \(\sin^2 x = \dfrac{1 - \cos 2x}{2}\), тогда \[\sqrt{8}\sin^2\dfrac{3\pi}{8} - \sqrt{2} = 2\sqrt{2}\cdot \dfrac{1 - \cos \dfrac{3\pi}{4}}{2} - \sqrt{2} = 2\sqrt{2}\cdot \dfrac{1 + \dfrac{\sqrt2}{2}}{2} - \sqrt{2} = \sqrt{2} + 1 - \sqrt{2} = 1\,.\]

Ответ: 1

Подставляя имеющиеся данные, получим \[16\cdot 3^{1,5} = 2\cdot V_2^{1,5}\qquad\Rightarrow\qquad 2^3\cdot 3^{1,5} = V_2^{1,5}\qquad\Rightarrow\qquad V_2 = 12\,.\]

Ответ: 12

Объём жидкости с погружённой деталью стал \(1500\cdot 1,4 = 2100\ куб.см\), следовательно, объём детали равен \(2100 - 1500 = 600\ куб.см\).

Ответ: 600

Расстояние, которое до места встречи проехал второй автомобиль, равно \(490 - 330 = 160\ км\), следовательно, он ехал в течение \(160 : 80 = 2\ ч\). Тогда первый автомобиль ехал до места встречи в течение \(2 + 1 = 3\ ч\), следовательно, его скорость равна \(330 : 3 = 110\ км/ч\).

Ответ: 110

ОДЗ: \(x \geqslant 0\).

1) \[y' = \dfrac{2}{3}\left(\sqrt{x} + \dfrac{x}{2\sqrt{x}}\right) - 4 = \sqrt{x} - 4\] Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[y' = 0\qquad\Leftrightarrow\qquad \sqrt{x} = 4\qquad\Leftrightarrow\qquad x = 16\,.\]

2) Найдём промежутки знакопостоянства \(y'\):

3) Найдём промежутки знакопостоянства \(y'\) на отрезке \([4; 16]\):

4) Эскиз графика \(y\) на отрезке \([4; 16]\):



Таким образом, наименьшего значения на отрезке \([4; 16]\) функция \(y\) достигает в \(x = 16\): \[y(16) = \dfrac{2}{3}\cdot 64 - 64 + \dfrac{1}{3} = -21\,.\]

Ответ: -21

а) ОДЗ: \(x\) – произвольный.

По формулам приведения и формуле косинуса двойного угла \(\cos 2x=2\cos^2x-1\): \[2\cos^2 x - 1 + \cos x = 0\]

Сделаем замену \(\cos x = t\): \[2t^2 - 1 + t = 0\qquad\Leftrightarrow\qquad 2(t - 0,5)(t + 1) = 0 \qquad\Leftrightarrow\qquad \left[ \begin{gathered} \begin{aligned} &t = -1\\ &t = 0,5 \end{aligned} \end{gathered} \right.\]

Сделаем обратную замену:

1) \(\cos x = -1\) равносильно \(x = \pi+2\pi n\), \(n\in\mathbb{Z}\).

2) \(\cos x = 0,5\) равносильно \(x = \pm \dfrac{\pi}{3} + 2\pi k\), \(k\in\mathbb{Z}\).

б) \(-2\pi \leqslant \pi+2\pi n \leqslant \dfrac{\pi}{2}\) равносильно \(-\dfrac32\leqslant n\leqslant -\dfrac{1}{4}\), но \(n\in\mathbb{Z}\), следовательно, среди этих решений подходит только решение при \(n = -1\): \(x = -\pi\).

\(-2\pi \leqslant \dfrac{\pi}{3} + 2\pi k_1 \leqslant \dfrac{\pi}{2}\) равносильно \(-\dfrac{7}{6} \leqslant k_1 \leqslant \dfrac{1}{12}\), но \(k_1\in\mathbb{Z}\), следовательно, среди этих решений подходят только решения при \(k_1 = -1\) и \(k_1=0\): \(x = -\dfrac{5\pi}{3}\) и \(x=\dfrac{\pi}3\).

\(-2\pi \leqslant -\dfrac{\pi}{3} + 2\pi k_2 \leqslant \dfrac{\pi}{2}\) равносильно \(-\dfrac{5}{6} \leqslant k_2 \leqslant \dfrac{5}{12}\), но \(k_2\in\mathbb{Z}\), следовательно, среди этих решений подходит только решение при \(k_2 = 0\): \(x = -\dfrac{\pi}{3}\).

Ответ:

а) \(\pi+2\pi n,\ n\in\mathbb{Z}\), \(\pm \dfrac{\pi}{3} + 2\pi k,\ k\in\mathbb{Z}\)

б) \(-\dfrac{5\pi}{3}\), \(-\pi\), \(-\dfrac{\pi}{3}\), \(\dfrac{\pi}{3}\)

а) Рассмотрим треугольник \(MBA\): \[MA^2 = 26 = 10 + 16 = (\sqrt{10})^2 + 4^2 = MB^2 + BA^2\,,\] следовательно, треугольник \(MBA\) прямоугольный и \(MB\perp AB\).

Рассмотрим треугольник \(MBC\): \[MC^2 = 235 = 10 + 225 = (\sqrt{10})^2 + 15^2 = MB^2 + BC^2\,,\] следовательно, треугольник \(MBC\) прямоугольный и \(MB\perp BC\).

Таким образом, \(AB \perp MB\perp BC\), то есть \(MB\) перпендикулярна двум пересекающимся прямым в плоскости \((ABCD)\), следовательно, \(MB\) – высота пирамиды \(MABCD\).

б) \[MB\perp (ABCD)\qquad\Rightarrow\qquad MB\perp AD;\qquad AB\perp AD\,,\] то есть \(AD\perp (MBA)\), следовательно, \(AM\) – проекция \(MD\) на плоскость \((MAB)\) и угол между \(MD\) и \((MAB)\) равен углу \(AMD\).

По теореме Пифагора в треугольнике \(MAD\): \[MD^2 = MA^2 + AD^2 = 26 + 225 = 251\qquad\Rightarrow\qquad MD = \sqrt{251}\,.\] Тогда \[\sin AMD = \dfrac{AD}{MD} = \dfrac{15}{\sqrt{251}}\qquad\Rightarrow\qquad \angle AMD = \arcsin \dfrac{15}{\sqrt{251}}\,.\]

Ответ:

б) \(\arcsin \dfrac{15}{\sqrt{251}}\)

ОДЗ: \[3^{x^2 - 1}\neq 1\qquad\Leftrightarrow\qquad x^2 - 1\neq 0\qquad\Leftrightarrow\qquad x\neq \pm 1\]

Решим на ОДЗ. Сделаем замену \(t = 3^{x^2 - 1} - 1\): \[1 - \dfrac{10}{t} + \dfrac{16}{t^2}\geqslant 0\qquad\Leftrightarrow\qquad \dfrac{t^2 - 10t + 16}{t^2}\geqslant 0\qquad\Leftrightarrow\qquad \dfrac{(t - 2)(t - 8)}{t^2}\geqslant 0\]

По методу интервалов



откуда \(t\in (-\infty; 0)\cup(0; 2]\cup[8; +\infty)\). Таким образом, \[\left[ \begin{gathered} 3^{x^2-1} - 1 < 0\\ 0 < 3^{x^2-1} - 1\leqslant 2\\ 3^{x^2-1} - 1\geqslant 8 \end{gathered} \right. \qquad\Leftrightarrow\qquad \left[ \begin{gathered} 3^{x^2-1} < 1\\ 1 < 3^{x^2-1} \leqslant 3\\ 3^{x^2-1} \geqslant 9 \end{gathered} \right. \qquad\Leftrightarrow\qquad \left[ \begin{gathered} x^2 - 1 < 0\\ 0 < x^2 - 1 \leqslant 1\\ x^2 - 1 \geqslant 2 \end{gathered} \right.\] что равносильно \[\left[ \begin{gathered} x^2 < 1\\ 1 < x^2 \leqslant 2\\ x^2 \geqslant 3 \end{gathered} \right. \qquad\Leftrightarrow\qquad \left[ \begin{gathered} x\in(-1; 1)\\ x\in[-\sqrt{2}; -1)\cup(1; \sqrt{2}]\\ x\in(-\infty; -\sqrt{3}]\cup[\sqrt{3}; +\infty) \end{gathered} \right.\] Тогда с учётом ОДЗ ответ: \[x\in (-\infty; -\sqrt{3}]\cup[-\sqrt{2}; -1)\cup(-1; 1)\cup(1; \sqrt{2}]\cup[\sqrt{3}; +\infty)\,.\]

Ответ:

\((-\infty; -\sqrt{3}]\cup[-\sqrt{2}; -1)\cup(-1; 1)\cup(1; \sqrt{2}]\cup[\sqrt{3}; +\infty)\)

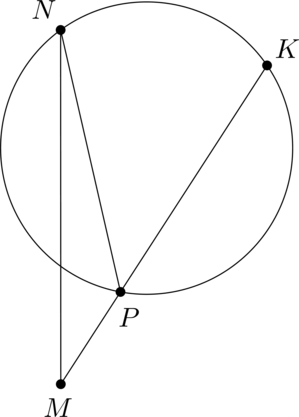
а) Пусть \(O_1\) и \(O_2\) центры большей и меньшей окружностей соответственно. Так как \(O_1M\) и \(O_2M\) перпендикулярны касательной, проходящей через точку \(M\), то точки \(O_1\), \(O_2\) и \(M\) лежат на одной прямой. Пусть \(M'\) – точка пересечения этой прямой с большей окружностью, отличная от \(M\).

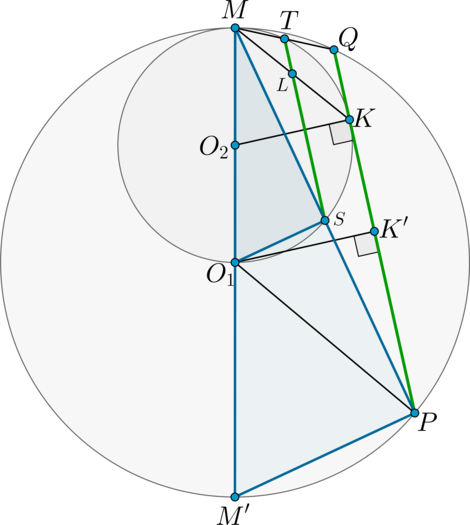
Докажем, что хорды данных окружностей, лежащие на одной прямой, проходящей через точку \(M\), относятся как их диаметры. Рассмотрим доказательство на примере хорд \(MS\) и \(MP\).

Рассмотрим треугольники \(MM'P\) и \(MO_1S\). Эти треугольники прямоугольные, так как \(MO_1\) – диаметр меньшей окружности (описанной около треугольника \(MO_1S\)), а \(MM'\) – диаметр большей окружности (описанной около треугольника \(MM'P\)). При этом острый угол \(O_1MS\) у них общий, следовательно, эти треугольники подобны.

Из подобия получаем требуемое: \[\dfrac{MS}{MP} = \dfrac{MO_1}{MM'}\]

Для других хорд, лежащих на прямой, проходящей через точку \(M\), утверждение доказывается аналогично.

Из доказанного следует, что \[\dfrac{MS}{MP} = \dfrac{MT}{MQ}\,.\]

Рассмотрим треугольники \(MST\) и \(MPQ\): \(\angle SMQ\) – общий, \(\dfrac{MS}{MP} = \dfrac{MT}{MQ}\), следовательно, эти треугольники подобны, откуда \(\angle MST = \angle MPQ\), следовательно, \(ST\parallel PQ\).

б) Опустим перпендикуляры \(O_1K'\) и \(O_2K\) на \(PQ\).

По теореме Пифагора \[K'O_1^2 = O_1P^2 - K'P^2\]

Так как \(O_1P = O_1Q\), то \(O_1K'\) – медиана в треугольнике \(PO_1Q\), следовательно, \(K'P = 3\), тогда \(K'O_1 = \sqrt{25 - 9} = 4\).

Так как \(MO_1\) – радиус большей окружности и диаметр меньшей, то радиус меньшей окружности равен \(0,5\cdot 5 = 2,5\)

Рассмотрим прямоугольную трапецию \(O_2O_1K'K\).

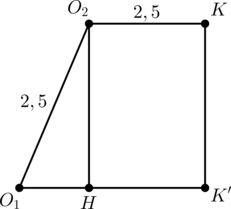
Пусть \(O_2H\) перпендикуляр к \(O_1K'\), тогда \(O_1H = O_1K' - O_2K = 4-2,5=1,5\), следовательно, по теореме Пифагора \(2 = O_2H = KK'\). Тогда \[PK = PK'+K'K=3+2=5,\qquad KQ = PK'-K'K=3-2=1.\]

Так как хорды данных окружностей, лежащие на одной прямой, проходящей через точку \(M\), относятся как их диаметры, то \(ST\) – средняя линия в треугольнике \(MPQ\), тогда \(SL\) – средняя линия в треугольнике \(MPK\) и \(LT\) – средняя линия в треугольнике \(MKQ\), следовательно, \[SL = 0,5PK=2,5,\qquad LT = 0,5KQ=0,5\,.\]

По теореме о произведении отрезков хорд \[ML\cdot LK = SL\cdot LT = 1,25=\dfrac54\,,\] откуда, с учётом равенства \(ML = LK\), получим \[ML = \dfrac{\sqrt{5}}{2}\,.\]

Ответ:

б) \(\dfrac{\sqrt{5}}{2}\)

Фраза “долг должен быть на одну и ту же сумму меньше” означает, что кредит выплачивается дифференцированными платежами. Следовательно, т.к. кредит взят на 11 месяцев, то эта “одна и та же сумма”, на которую уменьшается долг каждый месяц, равна \(\frac1{11}\) части от суммы кредита. Обозначим сумму кредита за \(A\) и составим таблицу.
Т.к. каждый месяц долг увеличивается на \(y\%\), то в первый месяц долг увеличиться на \(0,01y\cdot A\) рублей, то есть составит \(A+0,01yA\) рублей.
После выплаты долг должен уменьшиться на \(\frac1{11}A\) рублей, то есть должен составить \(\frac{10}{11}A\) рублей. Значит, выплата в первый месяц будет равна \(A+0,01yA-\frac{10}{11}A=0,01yA+\frac1{11}A\)

\[\begin{array}{|l|c|c|c|} \hline \text{Номер месяца}&\text{Долг после начисления }\%& \text{Долг после выплаты}&\text{Выплата}\\ \hline 1& A+0,01y\cdot A& \frac{10}{11}A& 0,01y\cdot A+\frac1{11}A\\ \hline 2& \frac{10}{11}A+0,01y\cdot \frac{10}{11}A& \frac{9}{11}A& 0,01y\cdot \frac{10}{11}A+\frac1{11}A\\ \hline 3& \frac9{11}A+0,01y\cdot \frac9{11}A& \frac8{11}A& 0,01y\cdot \frac9{11}A+\frac1{11}A\\ \hline \dots&\dots&\dots&\dots\\ \hline 10& \frac2{11}A+0,01y\cdot \frac2{11}A& \frac1{11}A& 0,01y\cdot \frac2{11}A+\frac1{11}A\\ \hline 11& \frac1{11}A+0,01y\cdot \frac1{11}A& 0& 0,01y\cdot \frac1{11}A+\frac1{11}A\\ \hline \end{array}\]

Заметим, что все выплаты состоят из двух частей, причем одна часть \(\left(\frac1{11}A\right)\) фиксирована.

По условию общая сумма выплат \(R\) превысила на \(30\%\) сумму кредита \(A\). Это значит, что переплата по кредиту \(R-A\) составляет \(30\%\) от \(A\). Найдем общую сумму выплат:

\(R=\left(0,01y\cdot A+\frac1{11}A\right)+\left(0,01y\cdot \frac{10}{11}A+\frac1{11}A\right)+ \left(0,01y\cdot \frac9{11}A+\frac1{11}A\right)+\dots+\)

\(+\left(0,01y\cdot \frac2{11}A+\frac1{11}A\right)+\left(0,01y\cdot \frac1{11}A+\frac1{11}A\right)=\)

\(=0,01y\cdot A\left(1+\frac{10}{11}+\frac9{11}+\dots+\frac2{11}+\frac1{11}\right)+11\cdot \frac1{11}A=\)

В скобке — сумма 11 членов арифметической прогрессии, где \(a_1=\frac1{11}, \ a_{11}=1\). По формуле \(S_{11}=\dfrac{a_1+a_{11}}2\cdot 11\), значит

\(=0,01y\cdot A\cdot \frac12\left(\frac1{11}+1\right)\cdot 11+A=0,06yA+A\)

Тогда переплата составила \(R-A=0,06yA\). Т.к. переплата составила \(30\%\) от \(A\), то

\[\dfrac{R-A}{A}\cdot 100\%=30\% \quad \Rightarrow \quad \dfrac{0,06yA}A=0,3 \quad \Rightarrow \quad y=5\]

Ответ:

\(5\)

Рассмотрим два случая:

1) \(4x - 2y - 10\geqslant 0\)
Первое уравнение системы в этом случае приводится к виду \[x^2 - 8x + y^2 + 4y + 13,75 = 0\qquad\Leftrightarrow\qquad (x - 4)^2 + (y + 2)^2 = 2,5^2\,.\]

Отдельно рассматриваемое данное уравнение задаёт на плоскости \((x; y)\) окружность с центром в точке \(O_1(4; -2)\) и радиусом \(2,5\), но с учётом условия \(4x - 2y - 10\geqslant 0\) нам подходит только часть этой окружности, лежащая в полуплоскости \(y \leqslant 2x - 5\).

2) \(4x - 2y - 10 < 0\)
Первое уравнение системы в этом случае приводится к виду \[x^2 + y^2 = 6,25\qquad\Leftrightarrow\qquad x^2 + y^2 = 2,5^2\,.\]

Отдельно рассматриваемое данное уравнение задаёт на плоскости \((x; y)\) окружность с центром в точке \(O(0; 0)\) и радиусом \(2,5\), но с учётом условия \(4x - 2y - 10 < 0\) нам подходит только часть этой окружности, лежащая в полуплоскости \(y > 2x - 5\).

Решая системы уравнений \[\begin{cases} (x - 4)^2 + (y + 2)^2 = 2,5^2\\ y = 2x - 5 \end{cases} \qquad \text{и}\qquad \begin{cases} x^2 + y^2 = 2,5^2\\ y = 2x - 5 \end{cases}\,,\] находим, что окружности из пунктов 1) и 2) пересекаются с прямой \(y = 2x - 5\) в точках \(C(2,5; 0)\) и \(D(1,5; -2)\).

При каждом фиксированном значении \(a\) второе уравнение исходной системы задаёт прямую, параллельную \(OO_1\) (при \(a = 0\) оно задаёт прямую \(OO_1\), а при \(a\neq 0\) прямую, полученную из \(OO_1\) параллельным переносом).

Найдём значение \(a\), при котором прямая \(y = 0,25a - 0,5x\) имеет с окружностью \(x^2 + y^2 = 2,5^2\) одну общую точку: \[x^2 + (0,25a - 0,5x)^2 = 2,5^2\qquad\Leftrightarrow\qquad 5(x^2 -0,2ax + 0,01a^2) + \dfrac{a^2}{4} - \dfrac{a^2}{20} = 25\,.\]

Чтобы данное уравнение имело единственное решение, необходимо и достаточно, чтобы левая часть представляла собой полный квадрат, откуда получим \(a^2 = 125\), то есть \(a = \pm 5\sqrt{5}\).

Проводя вычисления, можно показать, что при \(a = \pm 5\sqrt{5}\) окружность из пункта 2) также имеет с прямой \(y = 0,25a - 0,5x\) одну общую точку, то есть случаям \(\mathbf{1}\) и \(\mathbf{4}\) на рисунке отвечают прямые \(y = 0,25a - 0,5x\) при \(a = 5\sqrt{5}\) и \(a = -5\sqrt{5}\) соответственно.

Также легко показать, что случаям \(\mathbf{2}\) и \(\mathbf{3}\) отвечают прямые \(y = 0,25a - 0,5x\) при \(a = 5\) и \(a = -5\) соответственно.

Прямая \(y = 0,25a - 0,5x\) при \(a > 5\sqrt{5}\) не имеет общих точек с нарисованными дугами окружностей.
При \(a = 5\sqrt{5}\) эта прямая имеет две общие точки с этими дугами окружностей.
При \(5 < a < 5\sqrt{5}\) эта прямая имеет четыре общие точки с этими дугами окружностей.
При \(a = 5\) эта прямая имеет три общие точки с этими дугами окружностей.
При \(-5 < a < 5\) эта прямая имеет две общие точки с этими дугами окружностей.
При \(a = -5\) эта прямая имеет три общие точки с этими дугами окружностей.
При \(-5\sqrt{5} < a < -5\) эта прямая имеет четыре общие точки с этими дугами окружностей.
При \(a = -5\sqrt{5}\) эта прямая имеет две общие точки с этими дугами окружностей.
При \(a < -5\sqrt{5}\) эта прямая не имеет общих точек с этими дугами окружностей.

Таким образом, ответ: \[a\in (-5\sqrt{5}; -5]\cup[5; 5\sqrt{5})\,.\]

Ответ:

\((-5\sqrt{5}; -5]\cup[5; 5\sqrt{5})\)

а) Это могло быть, например, в случае, когда в категорию Б попадали изначально три человека, одному из которых было \(40\) лет, а двум другим по \(10\) лет. Тогда их средний возраст при первом опросе был \(20\) лет, а при втором опросе в категории Б остались только двое, которым исполнилось по \(14\) лет, то есть их средний возраст стал \(14\) лет.

б) Это могло быть, например, в случае, когда в категорию Б попадали те же трое, что в пункте а), а в категорию А изначально попадали два человека, которым было по \(70\) лет.

в) Пусть количество опрошенных, которые попадали в категорию А при первом опросе, было равно \(n\), а количество опрошенных, попадавших в категорию Б, было равно \(m\), тогда суммарный возраст участников при первом опросе составлял \(40(n + m)\), причём \[40(n + m) = 55n + 28m\qquad\Leftrightarrow\qquad 5n = 4m\,,\] откуда, в частности, следует, что \(n\) делится на \(4\), а \(m\) делится на \(5\).

Так как средний возраст в категории А вырос не на 4 года, то в категорию А должны были перейти опрошенные, которые ранее относились к категории Б. Пусть их ровно \(k\) человек. Так как при повторном опросе им могло быть не более \(44\) лет, то суммарный возраст участников категории А за счёт появления этих \(k\) человек не мог увеличиться более, чем на \(44k\), тогда \[57(n + k)\leqslant 59n + 44k\qquad\Rightarrow\qquad 2n\geqslant 13k\,.\]

Так как \(k \geqslant 1\), то \(n\geqslant 7\), но \(n\) делится на \(4\), следовательно, \(n\geqslant 8\). При \(n = 8\) имеем: \(m = 10\). Этот случай возможен только при \(k = 1\).

Проверим, подходит ли нам этот случай. Пусть возраст перешедшего в категорию А из категории Б стал \(41\leqslant x\leqslant 44\), тогда \[\begin{cases} 57(n + 1) = 59n + x\\ 31(m - 1) = 32m - x\,, \end{cases}\] откуда \(x = 41\) – подходит по условию.

Таким образом, менее \(18\) человек быть не могло, а \(18\) человек могло быть, например, так:
в первый раз опросили \(8\) человек, каждому из которых было по \(55\) лет, одного человека в возрасте \(37\) лет и \(9\) человек, каждому из которых было по \(27\) лет.

Ответ:

а) Да

б) Да

в) \(18\)