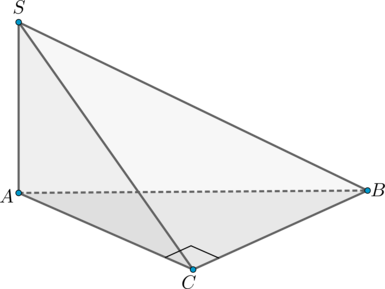
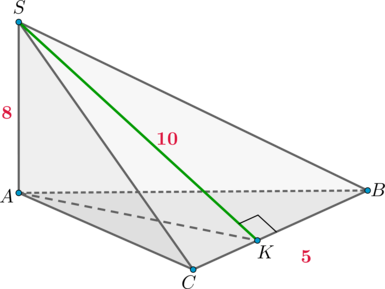
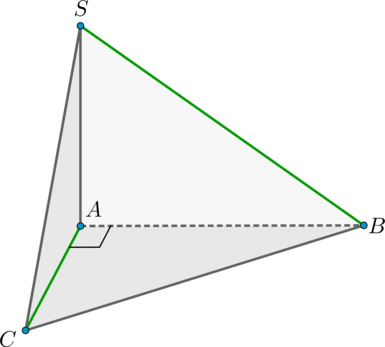
Пусть \(SABC\) – правильная треугольная пирамида с вершиной \(S\). Найдите угол между \(AS\) и \(BC\). Ответ дайте в градусах.
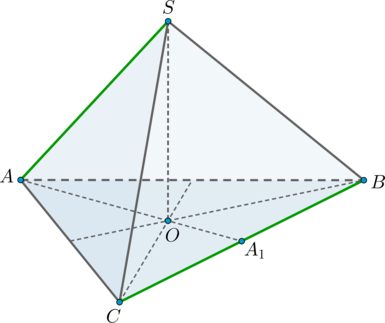
Так как пирамида правильная, то высота пирамиды \(SO\) падает в точку пересечения медиан основания. Пусть \(AA_1\) – медиана основания. Тогда \(AO\) – проекция наклонной \(AS\) на плоскость основания. Так как \(AO\) – часть \(AA_1\), а \(AA_1\perp BC\) (медианы правильного треугольника являются также и высотами), то по теореме о трех перпендикулярах (\(SO\perp (ABC), AO\perp BC\,\)) наклонная \(AS\) перпендикулярна \(BC\). Следовательно, \(\angle (AS, BC)=90^\circ\).
Ответ: 90