Найдите \(f(5)\), если \[f(x)=\dfrac x3+\dfrac 4x-\dfrac7{15}\]
Подставим вместо \(x\) число \(5\): \[f(5)=\dfrac 53+\dfrac 45-\dfrac7{15}=\dfrac{30}{15}=2\]
Ответ:
2
ДВИ в МГУ им. М. В. Ломоносова
Найдите \(f(5)\), если \[f(x)=\dfrac x3+\dfrac 4x-\dfrac7{15}\]
Подставим вместо \(x\) число \(5\): \[f(5)=\dfrac 53+\dfrac 45-\dfrac7{15}=\dfrac{30}{15}=2\]
Ответ:
2
Найдите сумму квадратов корней уравнения \[x^2-8x-3=0\]
По теореме Виета \(x_1+x_2=8\), \(x_1\cdot x_2=-3\), где \(x_1, x_2\) – корни квадратного трехчлена. Следовательно, \[x_1^2+x_2^2=x_1^2+2x_1x_2+x_2^2-2x_1x_2=(x_1+x_2)^2-2x_1x_2= 8^2-2\cdot (-3)=70\]
Ответ:
70
Решите неравенство \[\cos x-\sqrt2\cos 2x+\sin x\leqslant 0\]
Так как \(\cos 2x=\cos^2x-\sin^2x=(\cos x-\sin x)(\cos x+\sin x)\), то неравенство можно переписать в виде: \[(\cos x+\sin x)-\sqrt2(\cos x-\sin x)(\cos x+\sin x)\leqslant 0 \quad\Leftrightarrow\quad (\cos x+\sin x)(1-\sqrt2 (\cos x-\sin x))\leqslant 0\] Заметим, что \[\cos x-\sin x=\sqrt2\left(\dfrac 1{\sqrt2}\cos x- \dfrac1{\sqrt2}\sin x\right)=\sqrt2\cdot \cos \left(x+\dfrac{\pi}4\right),\] так как \(\dfrac1{\sqrt2}=\cos \dfrac{\pi}4=\sin \dfrac{\pi}4\). Аналогично \[\cos x+\sin x=\sqrt2\left(\dfrac 1{\sqrt2}\cos x+ \dfrac1{\sqrt2}\sin x\right)=\sqrt2\cdot \cos \left(x-\dfrac{\pi}4\right)\]Следовательно, неравенство примет вид: \[\cos \left(x-\dfrac{\pi}4\right)\cdot \left(\cos \left(x+\dfrac{\pi}4\right)-\dfrac 12\right)\geqslant 0 \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\begin{cases} \cos \left(x-\dfrac{\pi}4\right)\geqslant 0\\[2ex] \cos \left(x+\dfrac{\pi}4\right)\geqslant \dfrac12 \end{cases}\\[2ex] &\begin{cases} \cos \left(x-\dfrac{\pi}4\right)\leqslant 0\\[2ex] \cos \left(x+\dfrac{\pi}4\right)\leqslant \dfrac12 \end{cases} \end{aligned} \end{gathered}\right.\]
Рассмотрим каждую систему из совокупности по отдельности.
1) Решением неравенства \(\cos \left(x-\frac{\pi}4\right)\geqslant 0\) будут: \[-\dfrac{\pi}2+2\pi n\leqslant x-\dfrac{\pi}4\leqslant
\dfrac{\pi}2+2\pi n \quad\Leftrightarrow\quad -\dfrac{\pi}4+2\pi n
\leqslant x\leqslant \dfrac{3\pi}4+2\pi n, n\in\mathbb{Z}\] Решением неравенства \(\cos \left(x+\frac{\pi}4\right)\geqslant \frac12\) будут: \[-\dfrac{\pi}3+2\pi m\leqslant x+\dfrac{\pi}4\leqslant
\dfrac{\pi}3+2\pi m\quad\Leftrightarrow\quad -\dfrac{7\pi}{12}+2\pi
m\leqslant x\leqslant \dfrac{\pi}{12}+2\pi m, m\in\mathbb{Z}\] Пересечем полученные решения по окружности:
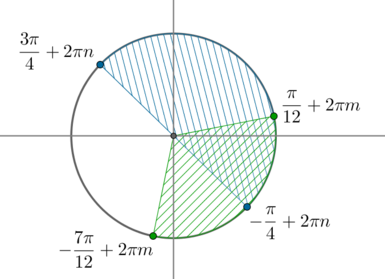
Таким образом, решением первой системы будут \[-\dfrac{\pi}4+2\pi n\leqslant x\leqslant \dfrac{\pi}{12}+2\pi n,
n\in\mathbb{Z}\]
2) Решением неравенства \(\cos \left(x-\frac{\pi}4\right)\leqslant 0\) будут: \[\dfrac{3\pi}4+2\pi n
\leqslant x\leqslant \dfrac{7\pi}4+2\pi n, n\in\mathbb{Z}\] Решением неравенства \(\cos \left(x+\frac{\pi}4\right)\leqslant \frac12\) будут: \[\dfrac{\pi}{12}+2\pi
m\leqslant x\leqslant \dfrac{17\pi}{12}+2\pi m, m\in\mathbb{Z}\] Пересечем полученные решения по окружности:
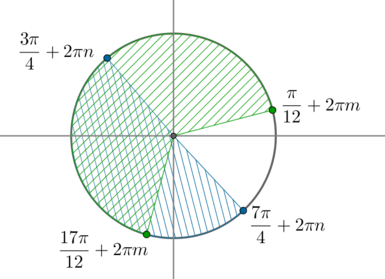
Таким образом, решением второй системы будут \[\dfrac{3\pi}4+2\pi n\leqslant x\leqslant \dfrac{17\pi}{12}+2\pi n,
n\in\mathbb{Z}\] Тогда ответом к исходному неравенству будут \[x\in \left[-\dfrac{\pi}4+2\pi n; \dfrac{\pi}{12}+2\pi n\right]
\cup\left[\dfrac{3\pi}4+2\pi n; \dfrac{17\pi}{12}+2\pi n\right] ,
n\in\mathbb{Z}\]
Ответ:
\(\left[-\dfrac{\pi}4+2\pi n; \dfrac{\pi}{12}+2\pi n\right] \cup\left[\dfrac{3\pi}4+2\pi n; \dfrac{17\pi}{12}+2\pi n\right] , n\in\mathbb{Z}\)
Решите уравнение \[\log_x|3x^2-4|=4\log_{|3x^2-4|}x\]
ОДЗ: \(x>0, x\ne 1, |3x^2-4|>0, |3x^2-4|\ne 1\).
Решим на ОДЗ. Сделаем замену: \(t=\log_x|3x^2-4|\). Так как \(\log_ab=\dfrac1{\log_ba}\) при \(a, b>0; a, b\ne 1\), то уравнение примет вид: \[t=\dfrac 4t \quad\Leftrightarrow\quad t^2=4\quad\Leftrightarrow
\quad t=\pm 2\] Сделаем обратную замену:
1) \(\log_x|3x^2-4|=2\). Тогда на ОДЗ получаем: \(|3x^2-4|=x^2\). Данное уравнение равносильно: \[\begin{cases} \left[\begin{gathered}\begin{aligned}
&3x^2-4=x^2\\
&3x^2-4=-x^2 \end{aligned}\end{gathered}\right.\\x^2\geqslant
0\end{cases} \quad\Leftrightarrow\quad
\left[\begin{gathered}\begin{aligned}
&x=\pm \sqrt2\\
&x=\pm 1 \end{aligned}\end{gathered}\right.\] 2) \(\log_x|3x^2-4|=-2\). Тогда на ОДЗ получаем: \(|3x^2-4|=x^{-2}\). Данное уравнение равносильно: \[\begin{cases} \left[\begin{gathered}\begin{aligned}
&3x^2-4=\dfrac1{x^2}\\[1ex]
&3x^2-4=-\dfrac1{x^2} \end{aligned}\end{gathered}\right.\\[2ex]
\dfrac1{x^2}\geqslant 0\end{cases} \quad\Leftrightarrow\quad
\left[\begin{gathered}\begin{aligned}
&x=\pm \sqrt{\dfrac{2+\sqrt7}3}\\[2ex]
&x=\pm \dfrac1{\sqrt3} \end{aligned}\end{gathered}\right.\]
Проверкой убеждаемся, что из полученных корней под ОДЗ подходят только \[x\in \left\{\dfrac1{\sqrt3}; \sqrt{\dfrac{2+\sqrt7}3}; \sqrt2\right\}\]
Ответ:
\(\left\{\dfrac1{\sqrt3}; \sqrt{\dfrac{2+\sqrt7}3}; \sqrt2\right\}\)
Окружность радиуса \(1,5\) касается середины стороны \(BC\) треугольника \(ABC\) и пересекает сторону \(AB\) в точках \(D\) и \(E\), так что \(AD:DE:EB=1:2:1\). Чему может равняться \(AC\), если \(\angle BAC=30^\circ\)?
Заметим, что из условия следует, что точки будут располагаться в следующем порядке: \(B, E, D, A\).
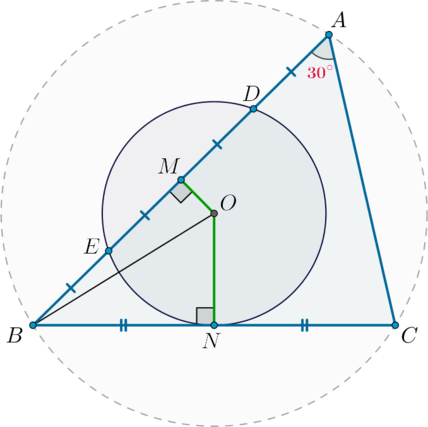
Проведем \(ON\perp BC\) и \(OM\perp AB\), где \(O\) – центр окружности. Следовательно, \(N\) – точка касания окружности и \(BC\), то есть \(BN=NC\). Так как радиус, перпендикулярный хорде, делит ее пополам, то \(EM=MD\). Следовательно, \(BE=EM=MD=DA\).
Значит, прямые \(ON\) и \(OM\) – серединные перпендикуляры к сторонам треугольника, следовательно, \(O\) – центр описанной окружности. Проведем \(OB\) – радиус данной описанной окружности.
Пусть \(BE=x\), \(BN=y\). Тогда, так как квадрат касательной равен произведению секущей на ее внешнюю часть, то \(y^2=x\cdot 3x\), следовательно, \(y=\sqrt3 x\).
\(BC=2y=2\sqrt3x\). По теореме синусов для \(\triangle ABC\): \[\dfrac{BC}{\sin \angle BAC}=2OB \quad\Rightarrow\quad
OB=2\sqrt3x\] Так как \(ON=1,5\) – радиус окружности (из условия), то по теореме Пифагора из \(\triangle BON\): \[BO^2=BN^2+ON^2 \quad\Rightarrow\quad x=\dfrac12\] Тогда \(AB=4x=2\), \(BC=\sqrt3\). Следовательно, по теореме косинусов из \(\triangle ABC\): \[BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot \cos30^\circ \quad\Rightarrow
\quad AC^2-2\sqrt3AC+1=0\quad \Rightarrow\quad AC=\sqrt3\pm \sqrt2\]
Ответ:
\(\sqrt3\pm \sqrt2\)
Велосипедист Василий выехал из пункта А в пункт Б. Проехав треть пути, Василий наткнулся на выбоину, вследствие чего велосипед безнадежно вышел из строя. Не теряя времени, Василий бросил сломавшийся велосипед и пошел пешком обратно в пункт А за новым велосипедом. В момент поломки из пункта А выехал мотоциклист Григорий. На каком расстоянии от пункта А он встретит Василия, если пункт Б отстоит от пункта А на \(4\) км, а Василий доберется до пункта А тогда же, когда Григорий до пункта Б? Скорости велосипеда, мотоцикла и пешехода считать постоянными.
Пусть \(x\) км/ч – скорость Василия, когда он шел пешком в пункт А за новым велосипедом. Пусть \(y\) км/ч – скорость Григория. На рисунке серыми штрихованными линиями разделен путь АБ на три равные части (так как Василий до поломки проехал треть пути), а красной штрихованной линией обозначено место встречи Василия и Григория.
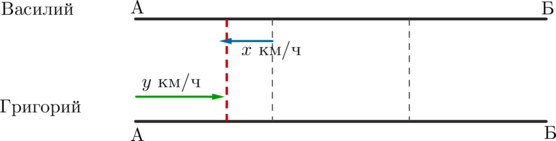
По условию время, за которое пешком Василий проходит треть пути, равно времени, за которое Григорий проходит весь путь. Следовательно, \[\dfrac{\frac43}{x}=\dfrac 4y \quad\Rightarrow\quad y=3x\] Таким образом, если \(t\) – время, которое двигался каждый до встречи (от начала движения Григория), то \(3xt+xt=\dfrac43\), откуда \(xt=\dfrac13\) – расстояние, которое прошел Василий. Следовательно, Григорий прошел \(3xt=1\) (км) – это и есть расстояние от пункта А до места встречи.
Заметим, что в данной задаче условие про то, что сначала Василий ехал на велосипеде, лишнее. На самом деле задача сводится к тому, что Василий и Григорий вышли одновременно из двух мест, расстояние между которыми равно \(\dfrac43\).
Ответ:
1 км
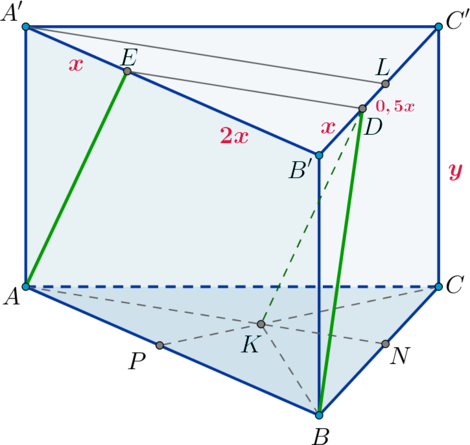
В правильную треугольную призму с основаниями \(ABC\) и \(A'B'C'\) и ребрами \(AA', BB', CC'\) вписана сфера. Найдите ее радиус, если известно, что расстояние между прямыми \(AE\) и \(BD\) равно \(\sqrt{13}\), где \(E\) и \(D\) – точки, лежащие на \(A'B'\) и \(B'C'\) соответственно, и \(A'E:EB'=B'D:DC'=1:2\).
1) Пусть \(3x\) – сторона основания, тогда \(A'E=x\), \(B'D=x\). Пусть \(y\) – боковое ребро призмы. Выразим расстояние между прямыми \(AE\) и \(BD\) через \(x, y\).
Заметим, что данные прямые являются скрещивающимися. Следовательно, проведем через прямую \(BD\) плоскость, параллельную прямой \(AE\), и найдем расстояние от \(AE\) до этой плоскости. Для этого проведем через точку \(D\) прямую, параллельную \(AE\). А для этого нужно найти плоскость, проходящую через \(A, E, D\).
Так как плоскость \(AED\) пересекает верхнее основание призмы по прямой \(ED\), то нижнее основание она пересечет по прямой, параллельной \(ED\). Найдем эту прямую.
Проведем через точку \(A'\) прямую \(A'L\), параллельную \(ED\). Тогда по теореме Фалеса \[A'E:EB'=LD:DB' \quad\Rightarrow\quad
LD=0,5x\quad\Rightarrow\quad B'L=LC'=1,5x\] Следовательно, \(A'L\) – медиана. Следовательно, если \(N\) – середина \(BC\), то \(AN\parallel
A'L\parallel ED\). Значит, \(AEDN\) – сечение призмы плоскостью \(AED\). В этой плоскости проведем \(DK\parallel AE\) (точка \(K\) будет лежать на \(AN\)). Следовательно, \(AE\parallel (KDB)\). Значит, необходимо найти расстояние от \(AE\) до плоскости \(KDB\). Оно равно расстоянию от любой точки прямой \(AE\) до плоскости \(KDB\).
2) Пусть \(h\) – расстояние от \(A\) до плоскости \(KDB\). Будем искать \(h\) через объем пирамиды \(AKDB\). С одной стороны, \(V_{AKDB}=\frac13\cdot h\cdot S_{KDB}\), а с другой стороны \(V_{AKDB}=\frac13 \cdot y\cdot S_{AKB}\).
Так как \(\triangle ABC\) – правильный, то \(AN=A'L=\frac32\sqrt3x\). Тогда из подобия \(\triangle A'B'L\sim \triangle EB'D\): \[ED=\dfrac23A'L=\sqrt3x.\] Следовательно, \(AK=ED=\sqrt3x\) (так как \(AEDK\) – параллелограмм по построению). Тогда \(KN=\frac12\sqrt3x\). Следовательно, \(AK:KN=2:1\), то есть \(K\) – точка пересечения медиан в \(\triangle ABC\). Тогда \(BK=AK\). Если \(P\) – середина \(AB\), то \(CP\) – медиана и высота, то есть \(KP\perp AB\). Значит, \[S_{AKB}=\dfrac12\cdot KP\cdot AB=\dfrac12\cdot \dfrac12\sqrt3x\cdot 3x=
\dfrac{3\sqrt3}4x^2\] Заметим, что \(BD=AE=KD=\sqrt{x^2+y^2}\). Тогда высота треугольника \(KDB\), опущенная из вершины \(D\) (на рисунке не отмечена), равна \[\sqrt{BD^2-\left(\frac12KB\right)^2}=\sqrt{\frac14x^2+y^2}\] Следовательно, \[S_{KDB}=\dfrac12\cdot \sqrt{\frac14x^2+y^2}\cdot \sqrt3x\] Таким образом, имеем: \[\dfrac 13\cdot h\cdot \dfrac12\cdot \sqrt{\frac14x^2+y^2}
\cdot \sqrt3x=\dfrac13\cdot y\cdot \dfrac{3\sqrt3}4x^2
\quad\Rightarrow\quad
h=\dfrac{3yx}{2\sqrt{\frac14x^2+y^2}}=\sqrt{13}
\quad\Rightarrow\quad 13x^2-9x^2y^2+52y^2=0\]
3) Так как сфера вписана в призму, то диаметр сферы равен высоте призмы, а радиус сферы равен радиусу окружности, вписанной в основание призмы.
Так как радиус окружности, вписанной в \(\triangle ABC\), равен \(KP=\frac12\sqrt3x\), то \[2\cdot \dfrac12\sqrt3x=y\quad\Rightarrow\quad y=\sqrt3x\] Подставляя полученный \(y\) в уравнение, найденное в пункте 2), получим \[x=\dfrac{13}{3\sqrt3}\] Следовательно, радиус сферы равен \[\dfrac12\cdot \sqrt3\cdot \dfrac{13}{3\sqrt3}=\dfrac{13}6\]
Ответ:
\(\dfrac{13}6\)
Найдите все пары \((\alpha, \beta)\), при которых достигается минимум выражения \[\dfrac{4-3\sin \alpha}{2+\cos 2\alpha}+ \dfrac{2+\cos 2\alpha}{\beta^2+\beta+1}+ \dfrac{\beta^2+\beta+1}{\sqrt{\beta}+1}+\dfrac{\sqrt{\beta}+1}{4-3\sin \alpha}\]
Среднее арифметическое \(n\) положительных чисел больше или равно среднему геометрическому этих чисел: \[\dfrac{a_1+a_2+\dots+a_n}n=\sqrt[n]{a_1a_2\dots a_n}\] Заметим, что каждая дробь в выражении – положительное число.
Так как \(\sin \alpha\in [-1;1]\), то \(4-3\sin \alpha\in [1;7]\). Так как \(\cos 2\alpha\in [-1;1]\), то \(2+\cos 2\alpha\in [1;3]\). Так как \(\sqrt{\beta}\geqslant 0\), то \(\sqrt{\beta}+1\geqslant 1\). Так как у квадратичного трехчлена \(\beta^2+\beta+1\) отрицательный дискриминант и коэффициент перед старшим членом положительный, то \(\beta^2+\beta+1>0\).
Заметим, что произведение всех четырех дробей равно \(1\). Следовательно, \[\dfrac{4-3\sin \alpha}{2+\cos 2\alpha}+
\dfrac{2+\cos 2\alpha}{\beta^2+\beta+1}+
\dfrac{\beta^2+\beta+1}{\sqrt{\beta}+1}+\dfrac{\sqrt{\beta}+1}{4-3\sin
\alpha}\geqslant 4\sqrt[4]{1}=4\] Тогда минимальное значение выражения равно \(4\) и оно будет достигаться, если все дроби равны \(1\).
Найдем \(\alpha\) из \[\dfrac{4-3\sin \alpha}{2+\cos 2\alpha}=1
\quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned}
&\alpha_1=\dfrac{\pi}2+2\pi n\\[2ex]
&\alpha_2=\dfrac{\pi}6+2\pi n\\[2ex]
&\alpha_3=\dfrac{5\pi}6+2\pi n \end{aligned}\end{gathered}\right. \
n\in\mathbb{Z}\] Из равенства четвертой дроби единице найдем \(\beta\).
1) При \(\alpha_1\) имеем: \[\sqrt{\beta}+1=4-3\cdot 1=1\quad\Rightarrow\quad \beta=0\] Подстановкой во вторую и третью дроби \(\alpha_1\) и \(\beta=0\) убеждаемся, что данные дроби равны \(1\). Следовательно, эти значения нам подходят.
2) При \(\alpha_2\) имеем: \[\sqrt{\beta}+1=4-3\cdot \dfrac12=\dfrac52\quad\Rightarrow \quad \beta=\dfrac94\] Подстановкой во вторую и третью дроби \(\alpha_2\) и \(\beta=\frac94\) убеждаемся, что вторая дробь не равна \(1\). Следовательно, эти значения нам не подходят.
3) При \(\alpha_3\) имеем: \[\sqrt{\beta}+1=4-3\cdot \dfrac12=\dfrac52\quad\Rightarrow \quad \beta=\dfrac94\] Аналогично подстановкой убеждаемся, что эти значения нам не подходят.
Ответ:
\(\alpha=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z} ; \ \beta=0\)