а) Решите уравнение \[\sin^3x+\cos^3x=0\]
б) Найдите все его корни, принадлежащие промежутку \(\left[-\dfrac{\pi}2; \pi\right].\)
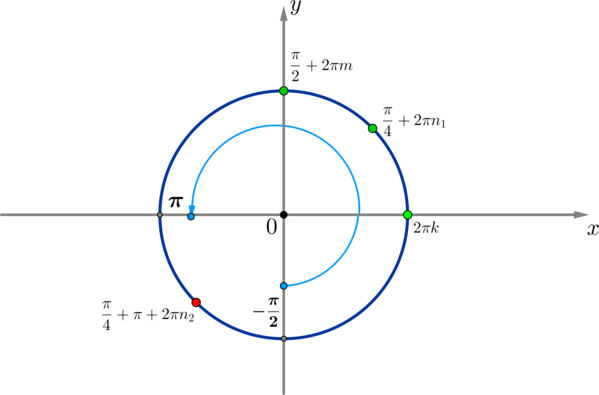
а) По формуле суммы кубов \(a^3+b^3=(a+b)(a^2-ab+b^2)\), а также учитывая, что \(\sin^2x+\cos^2x=1\), имеем: \[(\sin x+\cos x)(\sin^2x-\sin x\cos x+\cos^2x)=0\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\sin x+\cos x=0\\ &1-\sin x\cos x=0\end{aligned}\end{gathered}\right.\] Так как \(\sin x\cdot \cos x=0,5\sin 2x\), то \[\left[\begin{gathered}\begin{aligned} &\sin x=-\cos x \ \Big|:\cos x\\ &0,5\sin 2x=1\end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\mathrm{tg}\,x=-1\\ &\sin 2x=2\end{aligned}\end{gathered}\right.\] Второе уравнение не имеет решений, так как \(|\sin \alpha|\leqslant 1\) при любом \(\alpha\). Первое уравнение имеет решения: \[x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\]
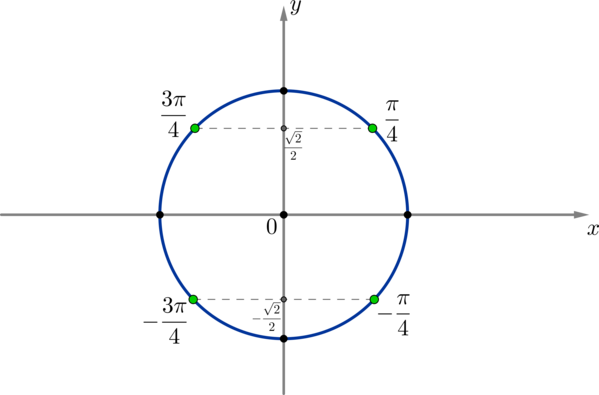
б) Отберем корни: \[-\dfrac{\pi}2\leqslant -\dfrac{\pi}4+\pi n\leqslant \pi \quad\Leftrightarrow \quad -\dfrac15\leqslant n\leqslant \dfrac54\quad\Rightarrow\quad n=0;1 \quad\Rightarrow\quad x=-\dfrac{\pi}4; \dfrac{3\pi}4\]
Ответ:
а) \(-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)
б) \(-\dfrac{\pi}4; \dfrac{3\pi}4\)