\(\blacktriangleright\) Теорема Менелая: пусть прямая пересекает треугольник в точке \(C_1\) на стороне \(AB\), в точке \(A_1\) на стороне \(BC\) и в точке \(B_1\) на продолжении стороны \(AC\). Тогда имеет место следующее соотношение:

\(\blacktriangleright\) Теорема, обратная теореме Менелая: пусть в треугольнике точка \(B_1\) лежит на продолжении стороны \(AC\), а точки \(A_1, C_1\) — на сторонах \(BC\) и \(AB\) соответственно. Тогда, если выполнено равенство \[\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_1}{C_1A}=1,\] то точки \(A_1, B_1, C_1\) лежат на одной прямой.

Теорема Чевы: пусть на сторонах треугольника \(ABC\) выбраны точки \(A_1\in BC, B_1\in AC, C_1\in AB\). Отрезки \(AA_1, BB_1, CC_1\) пересекаются в одной точке тогда и только тогда, когда выполнено равенство \[{\large{\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_1}{C_1A}=1}}\]

\(\blacktriangleright\) Теорема Стюарта: пусть в треугольнике на стороне \(AB\) отмечена точка \(P\). Тогда, если \(CP=p, AP=x, BP=y,AC=b, BC=a\), верно следующее соотношение:

\(\blacktriangleright\) С помощью теоремы Стюарта выводятся формулы нахождения биссектрис и медиан треугольника:

I. Если \(l_c\) — биссектриса, проведенная к стороне \(c\) и разбивающая эту сторону на отрезки \(x\) и \(y\), а \(a,b\) — две другие его стороны, то \[{\large{l^2_c=ab-xy}}\]

II. Если \(m_c\) — медиана, проведенная к стороне \(c\) треугольника, а \(a,b\) — две другие его стороны, то \[{\large{m^2_c=\dfrac{2a^2+2b^2-c^2}4}}\]

Ознакомиться с полной теорией

Задание 1 #2826

Уровень задания: Легче ЕГЭ

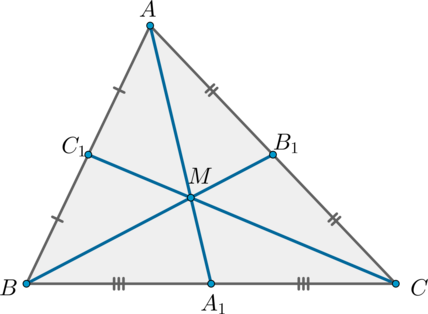
Докажите, что биссектрисы треугольника пересекаются в одной точке.

Показать решение

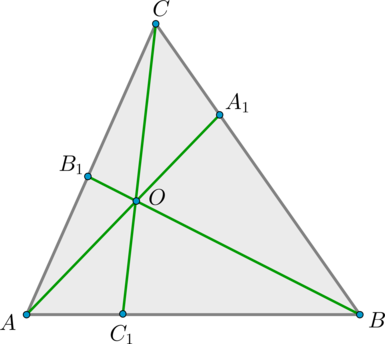
Пусть нам дан \(\triangle ABC\), проведем в нем биссектрисы \(AA_1, BB_1, CC_1\) и докажем что они пересекаются в одной точке.

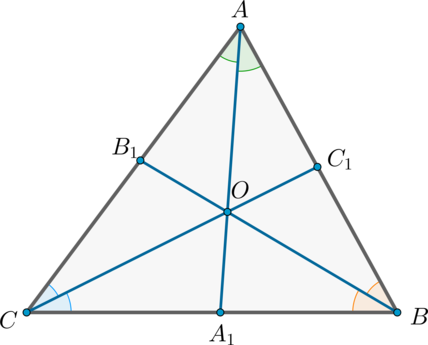
Воспользуемся свойством биссектрисы для всех трех биссектрис:

Для биссектрисы \(AA_1: \ \dfrac{BA_1}{A_1C} =\dfrac{AB}{AC}\)

Для биссектрисы \(BB_1: \ \dfrac{CB_1}{B_1A} =\dfrac{BC}{BA}\)

Для биссектрисы \(CC_1: \ \dfrac{AC_1}{C_1B} =\dfrac{CA}{CB}\)

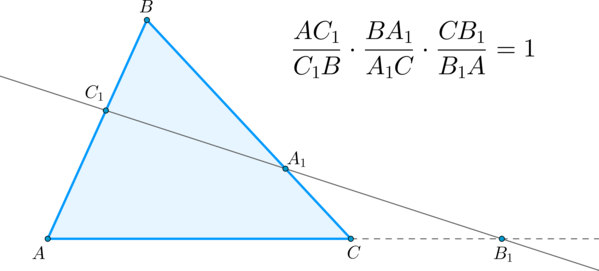
Воспользуемся теоремой Чевы: \[\dfrac{BA_1}{A_1C} \cdot \dfrac{CB_1}{B_1A} \cdot \dfrac{AC_1}{C_1B} = \dfrac{AB}{AC} \cdot \dfrac{BC}{BA} \cdot \dfrac{CA}{CB} = \dfrac{AB\cdot BC \cdot CA}{AB\cdot BC \cdot CA} =1.\]

Следовательно, биссектрисы треугольника пересекаются в одной точке.

Ответ:

Доказательство

Задание 2 #2827

Уровень задания: Легче ЕГЭ

Докажите, что высоты треугольника пересекаются в одной точке.

Показать решение

Пусть нам дан \(\triangle ABC\), проведем в нем высоты \(AA_1, BB_1, CC_1\) и докажем что они пересекаются в одной точке.

Заметим, что: \[\begin{aligned} &BA_1= \cos{\angle B} \cdot AB,\qquad A_1C= \cos{\angle C} \cdot AC,\\ &CB_1= \cos{\angle C} \cdot BC,\qquad B_1A= \cos{\angle A} \cdot AB,\\ &AC_1= \cos{\angle A} \cdot AC,\qquad C_1B= \cos{\angle B} \cdot BC. \end{aligned}\] Воспользуемся теоремой Чевы: \[\begin{aligned} &\dfrac{BA_1}{A_1C} \cdot \dfrac{CB_1}{B_1A} \cdot \dfrac{AC_1}{C_1B} = \dfrac{\cos{\angle B} \cdot AB}{\cos{\angle C} \cdot AC} \ \cdot \ \dfrac{\cos{\angle C} \cdot BC}{\cos{\angle A} \cdot AB} \ \cdot \ \dfrac{\cos{\angle A} \cdot AC}{\cos{\angle B} \cdot BC} =\\[1.5ex] = \ & \dfrac{AB\cdot BC \cdot CA \cdot \cos{\angle A} \cdot \cos{\angle B} \cdot \cos{\angle C}}{AB\cdot BC \cdot CA \cdot \cos{\angle A} \cdot \cos{\angle B} \cdot \cos{\angle C}} =1\,. \end{aligned}\]

Следовательно, высоты треугольника пересекаются в одной точке.

Ответ:

Доказательство

Задание 3 #2828

Уровень задания: Легче ЕГЭ

Докажите, что медианы треугольника пересекаются в одной точке.

Показать решение

Пусть нам дан \(\triangle ABC\), проведем в нем медианы \(AA_1, BB_1, CC_1\) и докажем что они пересекаются в одной точке.

Воспользуемся теоремой Чевы: \[\dfrac{AB_1}{B_1C} \cdot \dfrac{CA_1}{A_1B} \cdot \dfrac{BC_1}{C_1A} =\dfrac{1}{1} \cdot \dfrac{1}{1} \cdot \dfrac{1}{1} =1,\] так как \(A_1, \ B_1, \ C_1\) – середины сторон \(BC, \ AC, \ AB\) соответственно.
Следовательно, медианы треугольника пересекаются в одной точке.

Ответ:

Доказательство