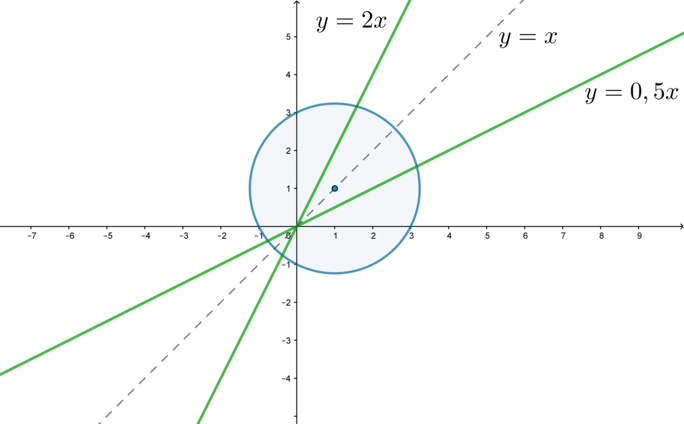
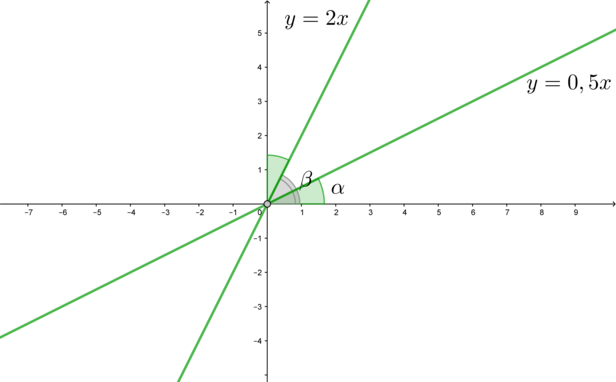
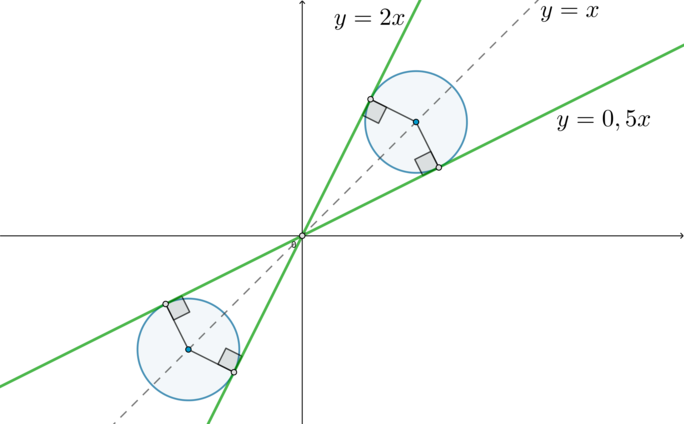
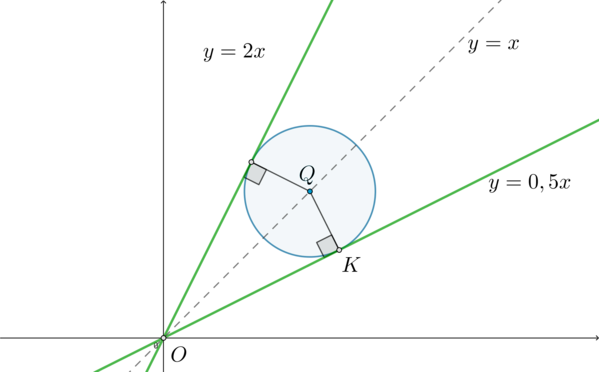
Найдите все значения параметра \(a\), при каждом из которых система \[\begin{cases} (x-2a-2)^2+(y-a)^2=1\\ y^2=x^2\end{cases}\]
имеет ровно четыре решения.
(ЕГЭ 2018, основная волна)
Второе уравнение системы можно переписать в виде \(y=\pm x\). Следовательно, рассмотрим два случая: когда \(y=x\) и когда \(y=-x\). Тогда количество решений системы будет равно сумме количества решений в первом и во втором случаях.
1) \(y=x\). Подставим в первое уравнение и получим: \[2x^2-2(3a+2)x+(2a+2)^2+a^2-1=0\quad(1)\] (заметим, что в случае \(y=-x\) мы поступим так же и тоже получим квадратное уравнение)
Чтобы исходная система имела 4 различных решения, нужно, чтобы в каждом из двух случаев получилось по 2 решения.
Квадратное уравнение имеет два корня, когда его \(D>0\). Найдем дискриминант уравнения (1):
\(D=-4(a^2+4a+2)\).
Дискриминант больше нуля: \(a^2+4a+2<0\), откуда \(a\in (-2-\sqrt2;
-2+\sqrt2)\).
2) \(y=-x\). Получаем квадратное уравнение: \[2x^2-2(a+2)x+(2a+2)^2+a^2-1=0\quad (2)\] Дискриминант больше нуля: \(D=-4(9a^2+12a+2)>0\), откуда \(a\in
\left(\frac{-2-\sqrt2}3; \frac{-2+\sqrt2}3\right)\).
Необходимо проверить, не совпадают ли решения в первом случае с решениями во втором случае.
Пусть \(x_0\) – общее решение уравнений (1) и (2), тогда \[2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=2x_0^2-2(a+2)x_0+(2a+2)^2+a^2-1\] Отсюда получаем, что либо \(x_0=0\), либо \(a=0\).
Если \(a=0\), то уравнения (1) и (2) получаются одинаковыми, следовательно, имеют одинаковые корни. Этот случай нам не подходит.
Если \(x_0=0\) – их общий корень, то тогда \(2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=0\), откуда \((2a+2)^2+a^2-1=0\), откуда \(a=-1\) или \(a=-0,6\). Тогда вся исходная система будет иметь 3 различных решения, что нам не подходит.
Учитывая все это, в ответ пойдут:
 \[a\in\left(\dfrac{-2-\sqrt2}3; -1\right)\cup\left(-1;
-0,6\right)\cup\left(-0,6; -2+\sqrt2\right)\]
\[a\in\left(\dfrac{-2-\sqrt2}3; -1\right)\cup\left(-1;
-0,6\right)\cup\left(-0,6; -2+\sqrt2\right)\]
Ответ:
\(a\in\left(\frac{-2-\sqrt2}3; -1\right)\cup\left(-1; -0,6\right)\cup\left(-0,6; -2+\sqrt2\right)\)