Уровень составитель ЕГЭ. Тренировочный вариант №4

\(T\cdot 1\) торт \(= T\cdot 8\) кусков торта \(= K\) кусков торта, откуда \(8\cdot T = K\), то есть \(\dfrac{K}{T} = 8\).

Ответ: 8

Координата материальной точки станет равна \(90\) через \(6\) секунд после начала движения.

Ответ: 6

Треугольники \(ABC\) и \(ACD\) подобны по двум углам (\(\angle B = \angle ACD\), \(\angle D = \angle BAC\)).
Так как в подобных треугольниках против равных углов лежат пропорциональные стороны, то
\(\dfrac{BC}{AC} = \dfrac{AC}{AD}\). Обозначим \(AC = x\), тогда имеем \[\dfrac{5}{x} = \dfrac{x}{20},\] откуда \(x^2 = 100\), следовательно, \(x = \pm 10\), но \(x > 0\), тогда \(x = 10\).

Ответ: 10

Так как рассматриваемые события независимы, то вероятность их одновременного наступления равна произведению их вероятностей. Тогда искомая вероятность равна \[0,4\cdot 0,4\cdot (1 - 0,4) = 0,096.\]

Ответ: 0,096

ОДЗ: \(3x^2 - 7 \neq 0\). Решим на ОДЗ:

Перенесём всё влево и приведём к общему знаменателю: \[\dfrac{20x - 3x^2 + 7}{3x^2 - 7} = 0.\] Дробь равна нулю в том и только том случае, когда её числитель равен нулю, а знаменатель отличен от нуля, тогда \(20x - 3x^2 + 7 = 0\), что равносильно \(3x^2 - 20x - 7 = 0\).

Дискриминант \[D = 400 + 84 = 484 = 22^2.\] Корни \[x_1 = \dfrac{20 + 22}{6} = 7, x_2 = \dfrac{20 - 22}{6} = -\dfrac{1}{3}\] – подходят по ОДЗ. Больший из корней равен \(7\).

Ответ: 7

\(OC\) – биссектриса \(\angle ACB\). Покажем это:
Построим радиусы \(OA\) и \(OB\).



Радиус, проведённый в точку касания, перпендикулярен касательной, следовательно
\(O\) – точка внутри угла \(ACB\), равноудалённая от его сторон. Тогда \(O\) лежит на биссектрисе этого угла (это можно показать через равенство треугольников \(AOC\) и \(BOC\)).

В данной задаче \(\angle OCB = 40^{\circ}\), тогда \(\angle ACB = 2\cdot \angle OCB = 2\cdot 40^{\circ} = 80^{\circ}\).

Ответ: 80

Для функции \(f(x)\), у которой производная в точке \(x_0\) имеет смысл, \(f'(x_0) < 0\) равносильно тому, что \(f(x)\) убывает в \(x_0\).

На интервале \((-0,5; 4,1)\) целыми являются точки \(0\), \(1\), \(2\), \(3\), \(4\). Среди этих точек \(f(x)\) убывает только в \(2\) и \(4\). Таким образом, производная функции \(y = f(x)\) отрицательна в \(2\) целых точках.

Ответ: 2

Так как площадь треугольника равна полупроизведению периметра на радиус вписанной окружности, то: \[V_{ABCD} = \dfrac{1}{3}\cdot S_{ABC}\cdot h = \dfrac{1}{3}\cdot\dfrac{P_{ABC}}{2}\cdot r\cdot h,\] но \(\dfrac{h}{r} = \dfrac{21}{8\pi}\), то есть \(h = \dfrac{21}{8\pi}r\), откуда \(\dfrac{1}{3}\cdot\dfrac{P_{ABC}}{2}\cdot r\cdot h = \dfrac{7r^2\cdot\pi}{7\cdot 8\pi} = 4,5\), тогда \(r^2 = 36\), значит, \(r = 6\).

\(h = \dfrac{21}{8\pi}r = \dfrac{63}{4\pi}\), следовательно, \(V_{\text{кон}} = \dfrac{1}{3}\pi\cdot r^2h = \dfrac{1}{3}\pi\cdot\dfrac{63}{4\pi}\cdot 36 = 189\).

Ответ: 189

По свойствам логарифма при \(\dfrac{x^2}{y^5} > 0\), \(1 \neq x^3 > 0\): \[\log_{x^3}\left(\dfrac{x^2}{y^5}\right) = \log_{x^3}x^2 - \log_{x^3}y^5 = \dfrac{1}{3}\cdot 2\log_{x}|x| - \dfrac{1}{3}\cdot 5\log_xy = \dfrac{2}{3} - \dfrac{5}{3}\cdot\log_{x}y.\] При \(\log_{x}y = 4\) получим \(\dfrac{2}{3} - \dfrac{5}{3}\cdot 4 = -6\).

Ответ: -6

Монетка будет находиться на высоте не менее \(11,2\) метра в те моменты \(t\), которые удовлетворяют неравенству \[1,2 + 15t - 5t^2 \geqslant 11,2\qquad\Leftrightarrow\qquad t^2 -3t + 2\leqslant 0.\] Решим это неравенство методом интервалов. Найдём корни уравнения \(t^2 -3t + 2 = 0\): \[t_1 = 1,\qquad\qquad t_2 = 2,\] тогда:



то есть монетка находилась на высоте не менее \(11,2\) метра в моменты \(t \in [1; 2]\), тогда она находилась на высоте не менее \(11,2\) метра в течение \(2 - 1 = 1\) секунды.

Ответ: 1

В \(2013\) году число не сдавших составило \(100\%-5\%=95\%\) от числа не сдавших в \(2012\) году, тогда в \(2013\) году не сдали ЕГЭ по математике \[20000 \cdot \dfrac{95}{100} = 19000 \ \text{выпускников}.\] В \(2014\) году число не сдавших составило \(100\%+17\%=117\%\) от числа не сдавших в \(2013\) году, тогда в \(2014\) не сдали ЕГЭ по математике \[19000 \cdot \dfrac{117}{100} = 22230\ \text{выпускника}.\]

Ответ: 22230

ОДЗ: \(x \neq -1\). Решим на ОДЗ:

1) \[y' = \left(\dfrac{x}{x+1}\cdot e^{-0,5x}\right)' = \dfrac{1}{(x + 1)^2}e^{-0,5x} - 0,5e^{-0,5x}\dfrac{x}{x + 1} = \dfrac{e^{-0,5x}}{(x + 1)^2}(-0,5x^2 - 0,5x + 1).\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{e^{-0,5x}}{(x + 1)^2}(-0,5x^2 - 0,5x + 1) = 0\qquad\Leftrightarrow\qquad -0,5x^2 - 0,5x + 1 = 0\] – на ОДЗ (так как \(e^t > 0\) при любом \(t\)), откуда находим корни \(x_1 = -2, \ x_2 = 1\). Производная функции \(y\) не определена при \(x = -1\), но \(x = -1\) не входит в ОДЗ. Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Эскиз графика \(y\):



Таким образом, \(x = -2\) – точка локального минимума функции \(y\).

Ответ: -2

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

а) Перепишем исходное уравнение при помощи основного тригонометрического тождества:

\[\begin{aligned} \sin^3{x} + 0,5 - 0,5\sin^2 x + \sin x = 1\qquad\Leftrightarrow\qquad \sin^3{x} - 0,5\sin^2 x + \sin x - 0,5 = 0. \end{aligned}\]

Последнее уравнение является уравнением третьей степени относительно \(\sin{x}\). Сделаем замену \(\sin x = t\): \[t^3 - 0,5t^2 + t - 0,5 = 0\qquad\Leftrightarrow\qquad t^2(t - 0,5) + (t - 0,5) = 0\qquad\Leftrightarrow\qquad (t^2 + 1)(t - 0,5) = 0.\] Так как \(t^2 + 1\geq 1 > 0\) при любом \(t\), то полученное уравнение равносильно \[t = 0,5,\] откуда \[\sin x = 0,5.\] Решения этого уравнения имеют вид \(x = \dfrac{\pi}{6} + 2\pi k\), \(x = \dfrac{5\pi}{6} + 2\pi k\), где \(k\in\mathbb{Z}\).

б) \[-\pi < \dfrac{\pi}{6} + 2\pi k < \pi\qquad\Leftrightarrow\qquad -\dfrac{7\pi}{6} < 2\pi k < \dfrac{5\pi}{6}\qquad\Leftrightarrow\qquad -\dfrac{7}{12} < k < \dfrac{5}{12},\] но \(k\in\mathbb{Z}\), тогда среди этих решений подходит только решение при \(k = 0\): \(x = \dfrac{\pi}{6}\).

\[-\pi < \dfrac{5\pi}{6} + 2\pi k < \pi\qquad\Leftrightarrow\qquad -\dfrac{11\pi}{6} < 2\pi k < \dfrac{\pi}{6}\qquad\Leftrightarrow\qquad -\dfrac{11}{12} < k < \dfrac{1}{12},\] но \(k\in\mathbb{Z}\), тогда среди этих решений подходит только решение при \(k = 0\): \(x = \dfrac{5\pi}{6}\).

Ответ:

а) \(\dfrac{\pi}{6} + 2\pi k\), \(\dfrac{5\pi}{6} + 2\pi k\), где \(k\in\mathbb{Z}\).

б) \(\dfrac{\pi}{6}\), \(\dfrac{5\pi}{6}\).

а)

Если прямая \(MN\parallel \alpha \Rightarrow MN\) параллельна некоторой прямой, лежащей в \(\alpha\). Проведем \(NS\perp BC, NS\cap KP=O\). В плоскости \(MNS\) проведем \(OH\parallel MN \Rightarrow MH=HS\). Тогда прямая \(KH\cap AB=T\). Так как плоскости \(ABC\) и \(A_1B_1C_1\) параллельны, то \(\alpha\) пересечет плоскость \(A_1B_1C_1\) по прямой, параллельной \(KT\). Следовательно, проведем \(PR\parallel KT\). Таким образом, \(TRPK\) – искомое сечение (трапеция).

б) Заметим, что \(CK=\dfrac{1}{6} \cdot 15=\dfrac{5}{2} \Rightarrow KS=5\). Т.к. \(MS\) – средняя линия треугольника \(ABC \Rightarrow MS=8 \Rightarrow HS=4\). Таким образом, по обратной теореме Пифагора треугольник \(HKS\) – прямоугольный, следовательно, \(\angle H =90^\circ\) и \(HK=3\). Таким образом, по теореме о трех перпендикулярах, из того, что \(NS\perp (ABC), HS\perp KT \Rightarrow OH\perp KT\).

Проведем \(PH_1 \perp KT\). Из подобия треугольников \(HOK\) и \(H_1PK\) следует, что \(PH_1=2OH\). Т.к. \(OS=\dfrac{1}{2}NS=4, HS=4 \Rightarrow OH=4\sqrt2\). Таким образом найдена высота трапеции \(PH_1=8\sqrt2\).

Найдем основания трапеции \(KT\) и \(PR\).

\(\sin \angle KSH = \dfrac{3}{5}=\sin \angle B=\dfrac{KT}{KB} \Rightarrow KT=\dfrac{15}{2}\).

\(\bigtriangleup PRB_1 \sim \bigtriangleup KTB \Rightarrow PR=\dfrac{3}{2}\).

Таким образом, \(S_{TRPK} = \dfrac{1}{2}\cdot (\dfrac{15}{2}+\dfrac{3}{2})\cdot 8\sqrt2 = 36\sqrt2\)

Ответ:

б) \(36\sqrt2\)

ОДЗ:

\[\begin{aligned} \begin{cases} x + \dfrac{\pi}{2} > 0\\ x + \dfrac{\pi}{2}\neq 1\\ x + 3 > 0 \end{cases} \qquad\Leftrightarrow\qquad \begin{cases} x > -\dfrac{\pi}{2}\\ x \neq -\dfrac{\pi}{2} + 1 \end{cases} \end{aligned}\]

Заметим, что \[x + 3 > x + \dfrac{\pi}{2} + 1\]

Рассмотрим два случая:
1) \(x > -\dfrac{\pi}{2} + 1\), тогда \[\log_{x + \frac{\pi}{2}} (x + 3) > 0\] и исходное неравенство равносильно \[x \leqslant 0,\] то есть в этом случае подходят \[x\in \left(-\dfrac{\pi}{2} + 1; 0\right]\] 2) \(-\dfrac{\pi}{2} < x < -\dfrac{\pi}{2} + 1\), тогда \[\log_{x + \frac{\pi}{2}} (x + 3) < 0\] и исходное неравенство равносильно \[x \geqslant 0,\] то есть в этом случае подходящих \(x\) нет.
В итоге ответ с учётом ОДЗ: \[x\in \left(-\dfrac{\pi}{2} + 1; 0\right]\,.\]

Ответ:

\(\left(-\dfrac{\pi}{2} + 1; 0\right]\)

а) Проведём диагонали \(AC\) и \(BD\).

Рассмотрим треугольники \(APS\) и \(ABD\): \(PS\) – средняя линия в треугольнике \(ABD\), тогда треугольники \(APS\) и \(ABD\) подобны, причём \(\dfrac{PS}{BD} = \dfrac{1}{2}\).

Аналогично \(\dfrac{QR}{BD} = \dfrac{1}{2}\), следовательно, \(PS = QR\).

Аналогично доказывается равенство \(PQ = RS\). В итоге в выпуклом четырёхугольнике \(PQRS\) противоположные стороны равны, тогда \(PQRS\) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.

б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.

Из подобия \(APS\) и \(ABD\) получаем: \[\dfrac{S_{APS}}{S_{ABD}} = \left(\dfrac{1}{2}\right)^2 = \dfrac{1}{4}.\]

Аналогично \(4S_{QCR} = S_{CBD}\), \(4S_{PBQ} = S_{ABC}\), \(4S_{SDR} = S_{ACD}\). Тогда \[S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.\] С другой стороны, \[S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},\] тогда \[S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} \qquad\Leftrightarrow\] \[S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = \dfrac{1}{2}S_{ABCD}.\] Но \(S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}\), откуда окончательно \[S_{PQRS} = \dfrac{1}{2}S_{ABCD}.\]

Таким образом, по взаимному расположению точек \(P\), \(Q\), \(R\), \(S\) однозначно восстанавливается площадь параллелограмма \(PQRS\), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках \(P\), \(Q\), \(R\) и \(S\).

В итоге \[\dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.\]

Ответ:

б) \(1\).

Составим таблицу пользования кредит в течение \(4\) лет (\(1\) и \(2\) - пока студент учится, \(3\) и \(4\) - пока студент выплачивает кредит), обозначив за \(t=1+0,01y, \ p=1+0,01\cdot 2y, \ A\) – стоимость годового обучения в ВУЗе, \(x\) – ежегодный платеж в последние два года: \[\begin{array}{|l|c|c|c|} \hline \text{Год} & \text{Сумма долга до начисления }\% & \text{Сумма долга после начисления }\%& \text{Сумма долга после платежа}\\ \hline 1& A&tA & \text{не вносит платеж}\\ \hline 2& tA+A&t(tA+A)=B &\text{не вносит платеж}\\ \hline 3& B&pB &pB-x\\ \hline 4& pB-x &p(pB-x) &p(pB-x)-x\\ \hline \end{array}\]

Т.к. в конце \(4\)-ого года кредит выплачен, то \(p(pB-x)-x=0 \ (*)\).

Заметим, что всего у банка было взято \(2A\) рублей (за \(2\) года обучения), а в итоге выплачено банку было \(2x\) рублей. Таким образом, переплата банку равна \(2x-2A\) рублей.

Необходимо, чтобы переплата составляла \(115,6 \%\) от суммы кредита, т.е. \(2x-2A=1,156\cdot 2A \Rightarrow x=2,156A\).

Выразим из \((*)\), чему равен ежегодный платеж \(x=\dfrac{p^2B}{p+1} \Rightarrow\)

\(\dfrac{p^2t(t+1)A}{p+1}=2,156A\) (обе части равенства можно разделить на \(A\)).

Сделав обратную замену \(t=1+0,01y, \ p=1+0,01\cdot 2y\), получим уравнение на \(y\): \[y^3 +300y^2 +22500y-578000=0.\]

Т.к. по условию сказано, что \(y\) - целое число, кратное пяти, то возможные значения \(y: 5, \ 10, \ 15, \ 20, \ 25, \cdots\)
Подставляя по очереди данные значения, находим, что наименьшее подходящее \(y=20 \%\).

Ответ:

\(20 \%\).

Пусть \(y=3x^3+ax+5\). Рассмотрим несколько случаев:

1) \(a=0\). Тогда уравнение имеет единственное решение \(x=-\sqrt[3]{\dfrac{5}{3}}\).

2) \(a>0\). Найдем производную \(y'=9x^2+a\). Т.к. \(a>0\), то \(y'>0\) при любых \(x\). Следовательно, функция \(y\) монотонно возрастает на всем \(\mathbb{R}\). Значит, имеет не более одной точки пересечения с осью \(Ox\).

Заметим, что \(y\left(-\dfrac{5}{a}\right)=-\dfrac{375}{a^3}<0; \ \ y(0)=5>0\), следовательно, на промежутке \(\left(-\dfrac{5}{a};0\right)\) есть точка \(x_o\), в которой \(y(x_o)=0\). Значит, \(x_o\) и есть единственное решение данного уравнения.

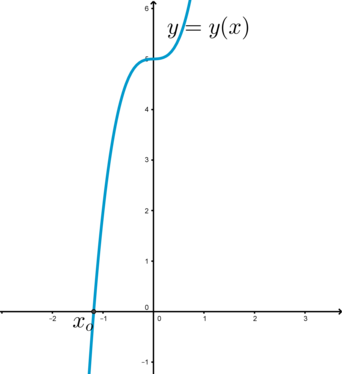
3) \(a<0\). Обозначим \(-a=b>0\).

Рассмотрим уравнение в виде \(3x^3=bx-5\). Обозначим \(f(x)=3x^3, \ g(x)=bx-5\). Найдем положительные значения \(b\), при которых функции \(f(x)\) и \(g(x)\) имеют ровно одну точку пересечения.

Найдем значения \(b\), при которых \(g(x)\) касается \(f(x)\):

\(f'(x)=9x^2\). Пусть \(x_o\) – точка касания. Тогда: \[\begin{cases} b>0\\ f'(x_o)=b\\ f(x_o)=g(x_o) \end{cases} \Rightarrow b=9\sqrt[3]{\dfrac{25}{36}}\]

Значит, при \(b=9\sqrt[3]{\dfrac{25}{36}}\) функции \(f(x)\) и \(g(x)\) имеют 2 точки пересечения, а при \(0<b<9\sqrt[3]{\dfrac{25}{36}}\) функции \(f(x)\) и \(g(x)\) имеют ровно одну точку пересечения (например, прямая, обозначенная пунктиром).

Тогда \(-9\sqrt[3]{\dfrac{25}{36}}<a<0\).

Значит, уравнение будет иметь единственный корень при \(a\in \left(-9\sqrt[3]{\dfrac{25}{36}}; +\infty\right)\).

Ответ:

\(a\in \left( -9\sqrt[3]{\dfrac{25}{36}}; +\infty \right)\).

\[\begin{aligned} &a^4x - 4a^2x + x^2 + a + 5x = 0\qquad\Leftrightarrow\qquad x^2 + (a^4 - 4a^2 + 5)x + a = 0\qquad\Leftrightarrow\\ &\Leftrightarrow\qquad x^2 + \bigl((a^2 - 2)^2 + 1\bigr)x + a = 0. \end{aligned}\]

По теореме Виета сумма корней этого уравнения (если у него они есть) равна \[(a^2 - 2)^2 + 1.\] Данное выражение будет наименьшим при \(a^2 = 2\), то есть при \(a = \pm\sqrt{2}\).

Остаётся только проверить, что при \(a = \pm\sqrt{2}\) у уравнения будут корни. При \(a = \sqrt{2}\): \[x^2 + x + \sqrt{2} = 0.\] Так как дискриминант \(D = 1 - 4\sqrt{2} < 0\), то у данного уравнения нет корней, следовательно, \(a = \sqrt{2}\) нам не подходит. При \(a = -\sqrt{2}\): \[x^2 + x - \sqrt{2} = 0.\] Так как дискриминант \(D = 1 + 4\sqrt{2} > 0\), то у данного уравнения есть два корня.
В итоге ответ: при \(a = -\sqrt{2}\).

Ответ:

\(-\sqrt{2}\)