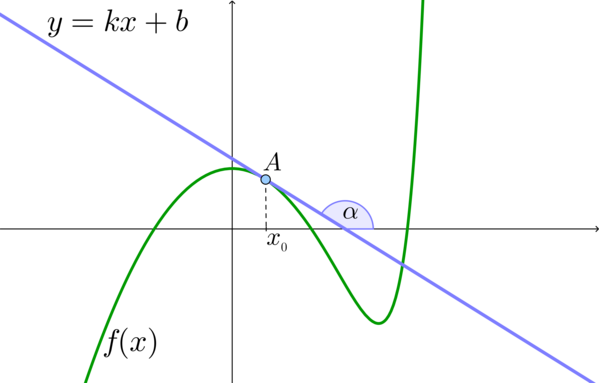
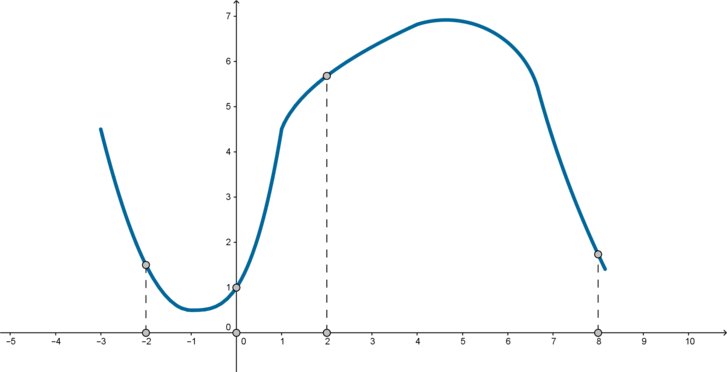
На рисунке изображены график функции \(y = f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
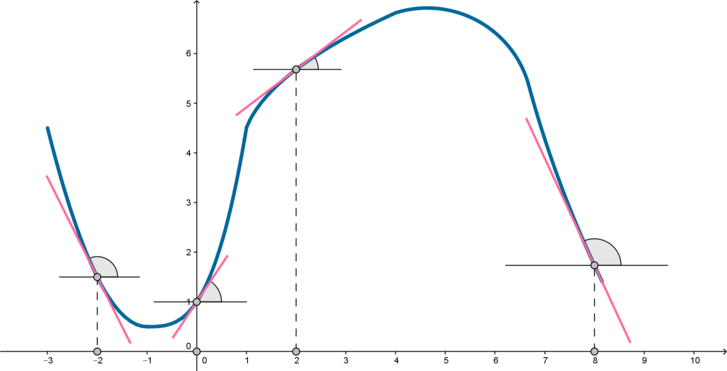
Производная функции \(f(x)\) в точке \(x_0\) равна тангенсу угла наклона касательной к графику \(f(x)\) в точке \((x_0; f(x_0))\) (то есть угла между касательной к графику \(f(x)\) в точке \((x_0; f(x_0))\) и положительным направлением оси \(Ox\)).
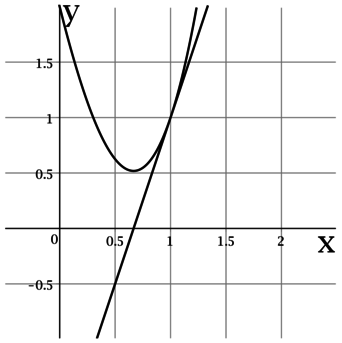
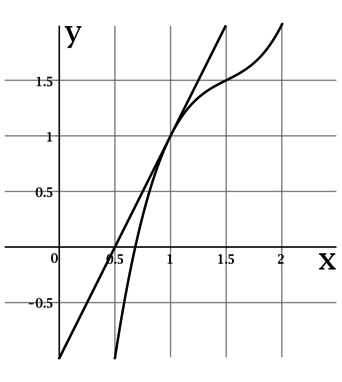
По рисунку видно, что касательная проходит через точки \((0,5; 0)\) и \((1; 1)\), тогда тангенс угла наклона касательной составляет \(1 : 0,5 = 2\), следовательно, \(f'(x_0) = 2\).
Ответ: 2