Нетипичные задачи в исследовании функций с помощью производной

\[y' = -4x^3 + 12x^2 - 2x + 2 = (-4x^3 + 11x^2) + (x^2 - 2x + 1) + 1 = x^2(11 - 4x) + (x - 1)^2 + 1\]

На отрезке \([0; 2]\) все слагаемые в полученной выше сумме неотрицательны, а последнее слагаемое даже положительно, следовательно, \(y' > 0\) на отрезке \([0; 2]\).

Таким образом, \(y\) возрастает на отрезке \([0; 2]\), следовательно, наибольшее на отрезке \([0; 2]\) значение рассматриваемая функция принимает при \(x = 2\): \[y(2) = -16 + 32 - 4 + 4 + 11 = 27\,.\]

Ответ: 27

1) \(y' = 15x^4 - 15x^2 - 180 = 15(x^4 - x^2 - 12)\).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[15(x^4 - x^2 - 12) = 0\qquad\Leftrightarrow\qquad x^4 - x^2 - 12 = 0\] – биквадратное уравнение, которое решается при помощи замены \(x^2 = t\), \(t\geq 0\). Корни уравнения после замены: \(t_1 = -3, \ t_2 = 4\), откуда находим \(x_1 = 2, \ x_2 = -2\). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Найдём промежутки знакопостоянства \(y'\) на отрезке \([-3; 3]\):



4) Эскиз графика \(y\) на отрезке \([-3; 3]\):



Значит \(x = -2\) – точка локального максимума и наибольшее значение функция достигает в ней или в \(x = 3\). Сравним эти значения:

\(y(-2) = -96 + 40 + 360 + 7 = 311\),

\(y(3) = 729 - 135 - 540 + 7 = 61 < 311\).

Итого: \(311\) – наибольшее значение функции \(y\) на \([-3; 3]\).

Ответ: 311

Так как \(-f^2(x)\leq 0\) при любом \(x\), то \(y = 7 - (e^x - 2)^2 \leq 7\), причём в \(x = \ln 2\) значение 7 достигается, \(0 \leq \ln 2 \leq 1\). Итого: наибольшее значение \(y\) на \([0; 1]\) равно 7.

Ответ: 7

1) \(y' = 15x^4 - 30x^2 + 15 = 15(x^2 - 1)^2 = 15(x - 1)^2(x + 1)^2\).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует):

\[15(x - 1)^2(x + 1)^2 = 0,\] откуда находим корни: \(x_1 = 1, \ x_2 = -1\). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Найдём промежутки знакопостоянства \(y'\) на отрезке \([-2; 100]\):



4) Эскиз графика \(y\) на отрезке \([-2; 100]\):



Значит точек локального минимума на \([-2; 100]\) нет, \(y\) на \([-2; 100]\) возрастает и, следовательно, наименьшее значение функция достигает в \(x = -2\).

\(y(-2) = -45\).

Итого: \(-45\) – наименьшее значение функции \(y\) на \([-2; 100]\).

Ответ: -45

\(y' = \sin 1\), следовательно, функция монотонна, тогда она принимает наибольшее значение в одном из концов отрезка. \(y\left(\dfrac{1}{\sin 1}\right) = 1 > 0 = y(0)\). Таким образом, наибольшее значение функции \(y\) на отрезке \(\left[0; \dfrac{1}{\sin 1}\right]\) равно 1.

Ответ: 1

ОДЗ: \(e^{x} + 1 > 0\). Так как \(e^{x} > 0\) при любом \(x\), то \(e^{x} + 1 > 0\), следовательно, \(x\) – произвольное. Решим на ОДЗ:

Заметим, что \(\ln^3{(e - 1)}\) и \(\ln{(e - 1)}\) – просто числа, тогда:

\[y' = \dfrac{e^x}{e^x + 1} + \dfrac{3x^2}{\ln^3{(e - 1)}} - 0,25.\]

Исследуем на наличие критических точек:

так как \[\left(\dfrac{e^x}{e^x + 1}\right)' = \dfrac{e^x}{(e^x + 1)^2} > 0,\] то \(\dfrac{e^x}{e^x + 1}\) возрастает, следовательно, на \([0; \ln{(e - 1)}]\) имеем: \[\dfrac{e^x}{e^x + 1} \geq \dfrac{e^0}{e^0 + 1} = 0,5,\] тогда на \([0; \ln{(e - 1)}]\) можно оценить \[y' = \dfrac{e^x}{e^x + 1} + \dfrac{3x^2}{\ln^3{(e - 1)}} - 0,25 \geq 0,5 + \dfrac{3x^2}{\ln^3{(e - 1)}} - 0,25 \geq 0,25 > 0,\] следовательно, критических точек у функции \(y\) на отрезке \([0; \ln{(e - 1)}]\) нет и функция \(y\) на нём возрастает.

Таким образом, наибольшее значение на \([0; \ln{(e - 1)}]\) функция достигает в \(x = \ln{(e - 1)}\).

\[y(\ln{(e - 1)}) = \ln{(e - 1 + 1)} + \dfrac{\ln^3{(e - 1)}}{\ln^3{(e - 1)}} = 2.\]

Итого: \(2\) – наибольшее значение функции \(y\) на \([0; \ln{(e - 1)}]\).

Ответ: 2

ОДЗ: \(x \neq -1\). Решим на ОДЗ:

1) \[y' = \left(\dfrac{x + 1 - x}{(x+1)^2} + \dfrac{x}{x+1}(2x - 2,5)\right)e^{x^2 - 2,5x + 2,25} = \dfrac{2x^3 - 0,5x^2 - 2,5x + 1}{(x+1)^2}e^{x^2 - 2,5x + 2,25}.\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{2x^3 - 0,5x^2 - 2,5x + 1}{(x+1)^2}e^{x^2 - 2,5x + 2,25} = 0\qquad\Leftrightarrow\qquad 2x^3 - 0,5x^2 - 2,5x + 1 = 0\] – на ОДЗ (так как \(e^t > 0\) при любом \(t\)).

У уравнения \(2x^3 - 0,5x^2 - 2,5x + 1 = 0\) можно подобрать решение \(x = 1\). В результате деления \(2x^3 - 0,5x^2 - 2,5x + 1\) на \((x - 1)\) получается \(2x^2 + 1,5x - 1\).

\[2x^3 - 0,5x^2 - 2,5x + 1 = (x - 1)(2x^2 + 1,5x - 1).\]

У уравнения \(2x^2 + 1,5x - 1 = 0\) два корня: \(x_1 = -\dfrac{3}{8} + \dfrac{\sqrt{41}}{8}, \ x_2 = -\dfrac{3}{8} - \dfrac{\sqrt{41}}{8}\). Производная функции \(y\) не определена при \(x = -1\), но \(x = -1\) не входит в ОДЗ.

Таким образом, \[y' = \dfrac{2\left(x+\dfrac{3}{8} - \dfrac{\sqrt{41}}{8}\right)\left(x+\dfrac{3}{8} + \dfrac{\sqrt{41}}{8}\right)(x-1)}{(x+1)^2}\cdot e^{x^2 - 2,5x + 2,25}.\] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

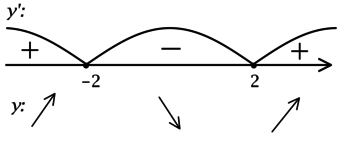
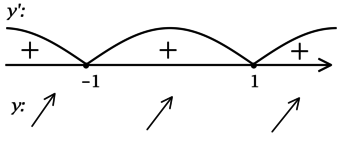
2) Найдём промежутки знакопостоянства \(y'\):



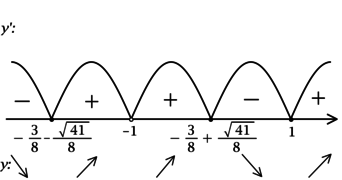
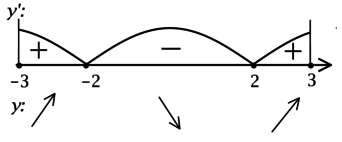
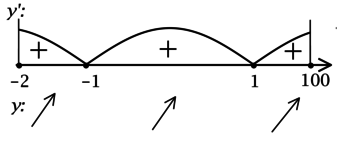
3) Найдём промежутки знакопостоянства \(y'\) на \([0; +\infty)\):



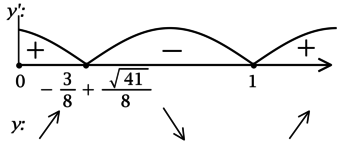
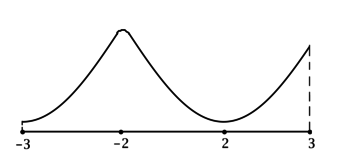
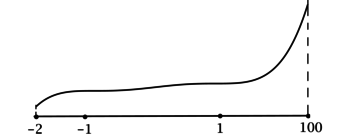
4) Эскиз графика \(y\) на \([0; +\infty)\):



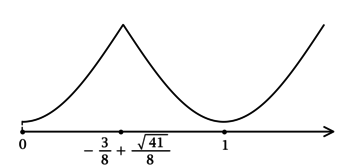
Значит \(x = 1\) – точка локального минимума и наименьшее значение на \([0; +\infty)\) функция \(y\) принимает в ней или в \(x = 0\). Сравним эти значения:

\(y(0) = 0\),

\(y(1) = 0,5 \cdot e^{0,75} > 0\). Итого: наименьшее значение функции \(y\) на \([0; +\infty)\) равно \(0\).

Ответ: 0