Дана пирамида \(SABC\) с вершиной \(S\), высота которой падает в точку пересечения биссектрис основания, являющегося равнобедренным треугольником с \(AC=CB\). Известно, что радиус вписанной в треугольник \(ABC\) окружности равен \(2-\sqrt3\), \(AB=2\), \(AS=2\sqrt2\). Найдите объем пирамиды.
1) 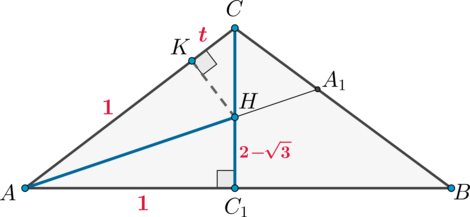
Пусть \(SH\) – высота пирамиды, то есть \(H\) – точка пересечения биссектрис основания. Рассмотрим основание \(ABC\). Так как центр вписанной в треугольник окружности лежит на пересечении биссектрис, то \(H\) – центр вписанной окружности. Пусть \(AA_1, CC_1\) – биссектрисы, тогда \(CC_1\) также медиана и высота, так как \(AC=CB\). Следовательно, \(HC_1\perp AB\), следовательно, \(HC_1=r\) и есть радиус вписанной окружности.
Проведем \(HK=r\perp AC\). Тогда \(AK=AC_1=1\). Пусть \(CK=t\). Тогда \(CC_1=\sqrt{AC^2-AC_1^2}=\sqrt{t(t+2)}\). Тогда из подобия \(\triangle
KCH\sim \triangle ACC_1\): \[\dfrac{HK}{AC_1}=\dfrac{CK}{CC_1} \quad\Rightarrow\quad
\dfrac{2-\sqrt3}1=\dfrac t{\sqrt{t(t+2)}} \quad\Rightarrow\quad
t=\dfrac2{\sqrt3}-1\] Следовательно, \(AC=t+1=\dfrac2{\sqrt3}\). Тогда \(CC_1=\dfrac1{\sqrt3}\).
Значит, площадь основания \[S_{ABC}=\dfrac12\cdot AB\cdot CC_1=\dfrac1{\sqrt3}.\]
2) 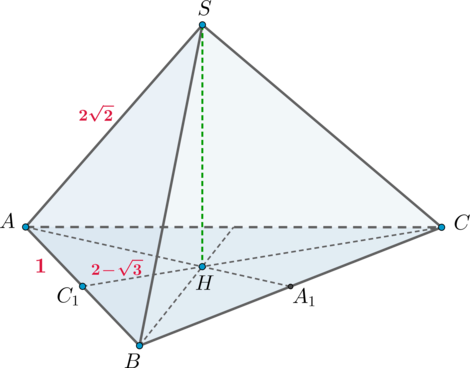
Заметим, что \(\triangle ASH\) прямоугольный, следовательно, для того, чтобы найти высоту пирамиды, нужно найти \(AH\). Из прямоугольного \(AC_1H\): \[AH^2=AC_1^2+C_1H^2=1+(2-\sqrt3)^2=4(2-\sqrt3).\] Следовательно, \[SH=\sqrt{AS^2-AH^2}=\sqrt{8-4(2-\sqrt3)}=\sqrt{4\sqrt3}=2\sqrt[4]3.\]
Следовательно, объем пирамиды равен \[V=\dfrac13\cdot SH\cdot S_{ABC}=\dfrac2{3\sqrt[4]3}.\]
Ответ:
\(\dfrac2{3\sqrt[4]3}\)