Задачи на тему «Параллелепипед», в которых учащимся предлагается найти объем многогранника и другие параметры при известных значениях граней, длины и диагоналей, являются обязательной частью ЕГЭ по математике. Это означает, что знать алгоритм вычисления правильного ответа должны выпускники с разным уровнем подготовки. Понимая принцип решения задач ЕГЭ на нахождение площади параллелепипеда, школьники смогут выполнять задания с любым количеством действий и при этом получить достаточно высокие баллы по итогам сдачи госэкзамена.
Базовая информация
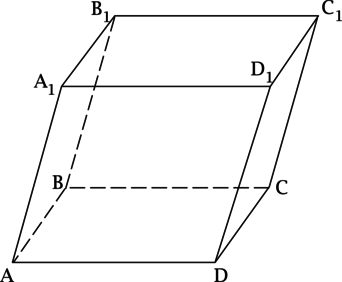
- Так как параллелепипедом называется призма, в основании которой находится параллелограмм, этот многогранник обладает всеми свойствами призмы.
- Фигура имеет 6 граней, причем те из них, которые параллельны друг другу, равны.
- Прямоугольный параллелепипед является прямым. В основании фигуры находится прямоугольник. Боковые грани многогранника также представляют собой прямоугольники.
- Объем параллелепипеда равен произведению площади основания на высоту призмы.
Занятия с образовательным порталом «Школково» — залог качественной подготовки к аттестационному испытанию
Зачастую проблема поиска необходимой информации встает перед старшеклассниками достаточно остро. Школьного учебника может просто не оказаться под рукой в нужный момент. А поиск формул для решения задач на определение объема и других параметров параллелепипеда может быть достаточно трудоемким даже в Интернете.
Весь необходимый для повторного изучения материал по данной теме вы найдете в этом разделе образовательного портала «Школково». Мы предлагаем учащимся и их преподавателям выстроить процесс подготовки к госэкзамену от простого к сложному. Такой подход позволит старшеклассникам понять, какие темы требуют более детального изучения, и улучшить имеющиеся знания.
В разделе «Теоретическая справка» подробно изложен весь базовый материал по теме «Параллелепипед». Представленная информация позволит вам восполнить пробелы в знаниях без помощи репетитора.
Чтобы задания ЕГЭ не вызывали сложностей, мы предлагаем также попрактиковаться в выполнении соответствующих упражнений. Найти подобные задания вы можете в разделе «Каталог». Здесь представлены как элементарные упражнения, так и материалы повышенной сложности, также изучаемые в рамках школьной программы. При этом каждая задача содержит подробный алгоритм решения и правильный ответ, например, задания по теме “Прямая и правильная призмы”.
Приступите к выполнению заданий уже сегодня, ведь с каждым днем остается все меньше времени на подготовку. А мы с удовольствием вам в этом поможем.