Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как подготовиться к экзамену?
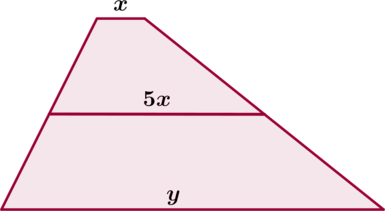
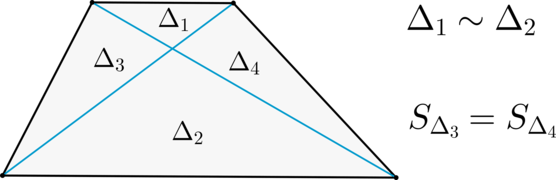
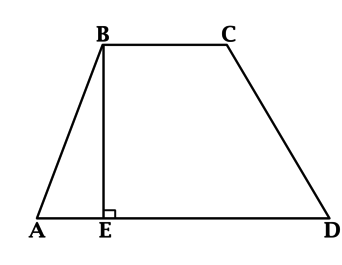
Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.
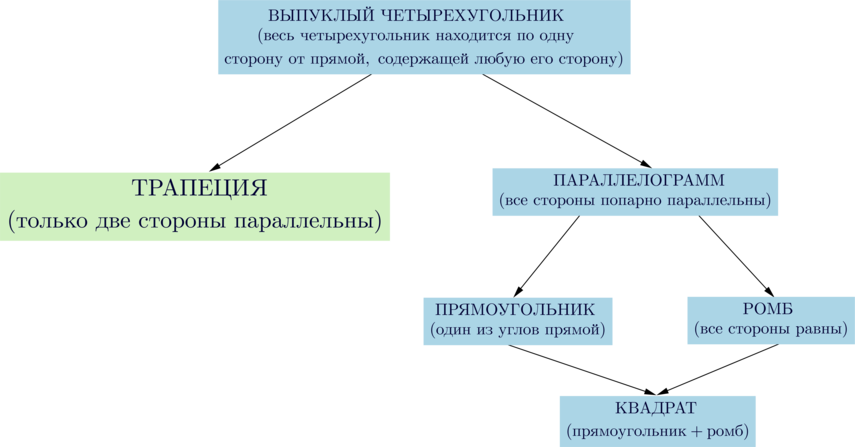
Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».
«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.