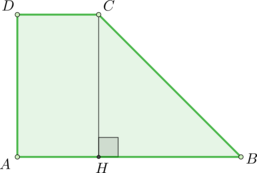
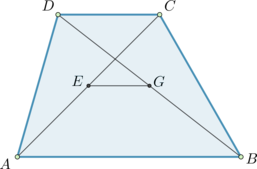
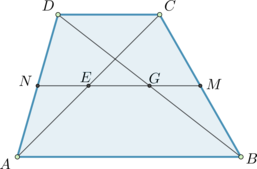
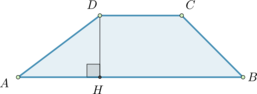
В трапеции \(ABCD\) с основаниями \(AD\) и \(BC\): отрезки \(QR\) и \(PS\) параллельны основаниям, причем \(AP = QB\) и \(CR = SD\). Найдите основание \(BC\), если \(QR = 6,75\), \(PS = 8,25\), а \(AD = 12\).
Т.к. \(QR\) и \(PS\) параллельны основаниям, то четырехугольник \(PQRS\) также будет трапецией, причем среднии линии \(ABCD\) и \(PQRS\) совпадают. Средняя линия равна \(\frac{1}{2}\cdot(QR + PS) = \frac{1}{2}\cdot(6,75 + 8,25) = 7,5\). Тогда можно выразить верхнее основание через среднюю линию и нижнее основание следующим образом: \(BC = 2\cdot7,5 - 12 = 3\).
Ответ: 3