Вычислите значение функции \[x^2-0,625x-\dfrac18\]
в точке \(x=\dfrac45\).
Подставим вместо \(x=\dfrac45\): \[\dfrac{16}{25}-\dfrac{625}{1000}\cdot \dfrac45-\dfrac 18= \dfrac{16}{25}-\dfrac12-\dfrac18=\dfrac3{200}=0,015\]
Ответ:
0,015
ДВИ в МГУ им. М. В. Ломоносова
Вычислите значение функции \[x^2-0,625x-\dfrac18\]
в точке \(x=\dfrac45\).
Подставим вместо \(x=\dfrac45\): \[\dfrac{16}{25}-\dfrac{625}{1000}\cdot \dfrac45-\dfrac 18= \dfrac{16}{25}-\dfrac12-\dfrac18=\dfrac3{200}=0,015\]
Ответ:
0,015
Решите уравнение \[(\sin x+\cos x)^2=1\]
Данное уравнение равносильно \[\sin x+\cos x=\pm 1 \ \Big| \cdot \dfrac1{\sqrt2}\quad
\Leftrightarrow\quad \sin x\cdot \dfrac1{\sqrt2}+\cos x\cdot
\dfrac1{\sqrt2}=\pm \dfrac1{\sqrt2}\quad\Leftrightarrow\quad \sin
\left(x+\dfrac{\pi}4\right)=\pm\dfrac1{\sqrt2}\] Если \(x+\dfrac{\pi}4=y\), то уравнение примет вид: \[\sin y=\pm \dfrac1{\sqrt2}\] Решим данное уравнение с помощью окружности:
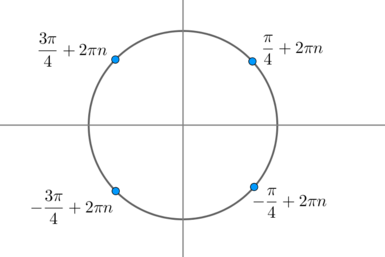
Все полученные углы можно объединить в одну запись: \[y=\dfrac{\pi}4+\dfrac{\pi}2 k\quad\Rightarrow\quad x=\dfrac{\pi}2 k ,
k\in\mathbb{Z}\]
Ответ:
\(\dfrac{\pi}2 k, k\in\mathbb{Z}\)
Решите уравнение \[\log_2(3x-4)=\log_4(2-x)\]
ОДЗ уравнения: \(3x-4>0\) и \(2-x>0\), что равносильно \(\dfrac{12}9<x<2\).
Решим уравнение на ОДЗ.
Так как на ОДЗ \(\log_ab=\log_{a^2}b^2\), то уравнение примет вид: \[\log_4(3x-4)^2=\log_4(2-x)\quad\Rightarrow\quad
(3x-4)^2=2-x\quad\Rightarrow\quad 9x^2-23x+14=0\] Заметим, что \(x=1\) является корнем полученного уравнения. Следовательно, по теореме Виета второй корень равен \[x=\dfrac{14}9:1=\dfrac{14}9\] Заметим, что \(x=1\) не подходит по ОДЗ, \(x=\dfrac{14}9\) – подходит по ОДЗ.
Ответ:
\(\dfrac{14}9\)
Решите неравенство \[\dfrac{\sqrt{5x+3}-1}{\sqrt{3x+2}-1}>1\]
ОДЗ числителя и знаменателя левой части: \(5x+3\geqslant 0\) и \(3x+2\geqslant 0\), что равносильно \(x\geqslant -\dfrac35\).
Решим на ОДЗ. \[\dfrac{\sqrt{5x+3}-\sqrt{3x+2}}{\sqrt{3x+2}-1}>0
\quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned}
&\begin{cases} \sqrt{3x+2}-1>0\\
\sqrt{5x+3}>\sqrt{3x+2} \end{cases}\\
&\begin{cases} \sqrt{3x+2}-1<0\\
\sqrt{5x+3}<\sqrt{3x+2}\end{cases}
\end{aligned}\end{gathered}\right.\] Решением первой системы, учитывая ОДЗ, будут \[\begin{cases} x>-\dfrac13\\[1ex]
x>-\dfrac12\\[1ex]
x\geqslant -\dfrac35 \end{cases}\quad\Rightarrow\quad x>-\dfrac13\] Решением второй системы, учитывая ОДЗ, будут \[\begin{cases} x<-\dfrac13\\[1ex]
x<-\dfrac12\\[1ex]
x\geqslant -\dfrac35 \end{cases}\quad\Rightarrow\quad
-\dfrac35\leqslant x<-\dfrac12\]
Ответ:
\(\left[-\dfrac35; -\dfrac12\right)\cup \left(-\dfrac13;+\infty\right)\)
Медианы \(AL\) и \(BM\) треугольника \(ABC\) пересекаются в точке \(K\). Найдите длину отрезка \(CK\), если \(AB=\sqrt3\) и известно, что вокруг четырехугольника \(KLCM\) можно описать окружность.
Рассмотрим чертеж:
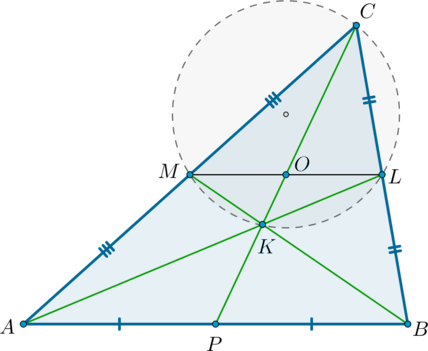
Проведем медиану \(CP\) и среднюю линию \(ML\) (\(\Rightarrow ML\parallel
AB\)). Пусть \(O=CP\cap ML\). По теореме Фалеса \(CO=OP\). Следовательно, \(MO=0,5AP=0,25AB=0,5PB=OL\), то есть \(MO=OL=\frac{\sqrt3}4\).
Так как \(\triangle MOK\sim \triangle BPK\) с коэффициентом подобия \(\frac12\), то \(OK=\frac12KP\). Обозначим \(OK=x\), тогда \(KP=2x\). Так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \(CK:KP=2:1\), следовательно, \(CK=4x\), значит, \(CO=3x\).
Так как в окружности произведения отрезков пересекающихся хорд равны, то \[MO\cdot OL=CO\cdot OK\quad\Rightarrow\quad \dfrac3{16}=3x^2
\quad\Rightarrow\quad x=\dfrac14\ ({\small{\text{т.к.}}} \ x>0)\] Тогда \[CK=4x=1.\]
Ответ:
1
Найдите наибольшее из значений функции \[\dfrac{9^x}{4^x-6^x+9^x}\]
и точку \(x\), в которой это значение достигается.
Пусть \[y=\dfrac{9^x}{4^x-6^x+9^x}\] Разделим числитель и знаменатель функции на \(9^x\) (при этом заметим, что так как \(9^x>0\), то область значений и область определения функции не изменятся): \[y=\dfrac1{\left(\frac23\right)^{2x}-\left(\frac23\right)^x+1}\] Обозначим \(\left(\frac23\right)^x=t\).
Тогда \[y(t)=\dfrac1{t^2-t+1}\] Заметим, что наибольшее значение \(y(t)\) будет принимать при наименьшем значении выражения \(t^2-t+1\). Рассмотрим функцию \[g(t)=t^2-t+1\] Графиком данной функции является парабола, ветви которой направлены вверх. Следовательно, наименьшее значение функция \(g\) принимает в вершине параболы. \[t_{\text{верш}}=\dfrac12\quad\Rightarrow\quad
g_{min}=g\left(\frac12\right)=\dfrac34\] Таким образом, \[y_{max}=\dfrac1{g_{min}}=\dfrac43\] Найдем \(x\), при котором принимается это значение.
Так как наибольшее значение \(y(t)\) принимает при \(t=\frac12\), а \(t=\left(\frac23\right)^x\), то \[x=\log_{\frac23}\left(\dfrac12\right)\]
Ответ:
\(y_{max}=\dfrac43\) при \(x=\log_{\frac23}\left(\dfrac12\right)\)
В закрытой коробке, имеющей форму куба со стороной \(5\), лежат два шара. Радиус первого из них равен \(2\). Этот шар касается плоскости основания и двух соседних боковых граней куба. Второй шар касается двух других боковых граней куба, плоскости основания и первого шара. Чему равен радиус второго шара?
Рассмотрим картинку:
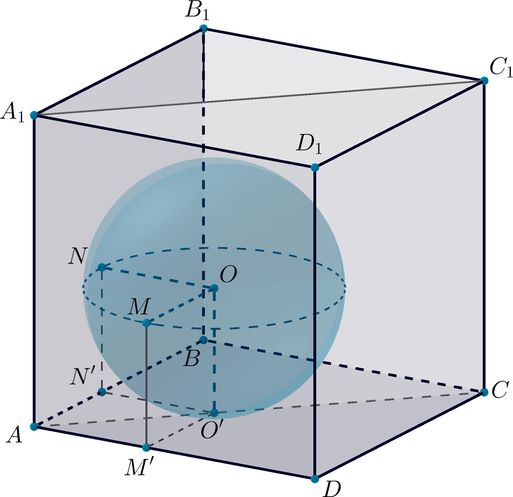
Заметим, что так как первый шар касается двух соседних боковых граней куба, то центр шара лежит в плоскости, делящей двугранный угол, образованный соседними гранями \(AA_1B_1B\) и \(AA_1D_1D\), пополам. То есть центр шара лежит в диагональной плоскости \(AA_1C_1C\) куба. Если спроецировать центр \(O\) шара на плоскость нижнего основания \(ABC\), то мы получим точку \(O'\) на диагонали \(AC\) основания. Если \(M, N\) – точки касания шара с боковыми гранями, то \(M', N'\) – их проекции, причем \(O'M'\perp AD, O'N'\perp AB, O'M'=O'N'=OO'=2\).
Следовательно, \(AM'=AN'=2\), следовательно, \(AO'=\sqrt{AM'^2+M'O'^2}=2\sqrt2\).
Так как второй шар касается двух других граней и основания, то он может касаться двух других граней и верхнего основания или двух других граней и нижнего основания. Причем в обоих случаях центр \(Q\) второго шара будет находиться в плоскости \(AA_1C_1C\).
1) Пусть второй шар касается нижнего основания. Схематично это выглядит так:
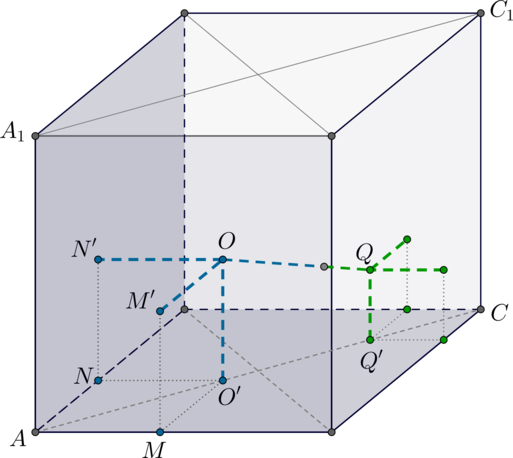
Так как оба шара к тому же касаются друг друга, то \(OQ\) равно сумме радиусов. Пусть радиус второго шара \(x\). Тогда \(OQ=2+x\). Из найденного \(AO'=2\sqrt2\), аналогично \(CQ'=x\sqrt2\). Так как \(AC=5\sqrt2\), то \(O'Q'=3\sqrt2-x\sqrt2\):
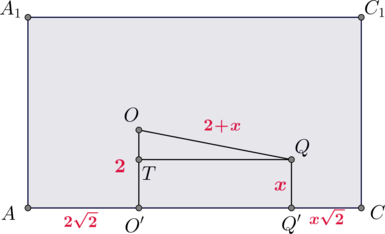
Тогда \(O'OQQ'\) – прямоугольная трапеция. Проведем \(QT\perp OO'\). Тогда \(\triangle OTQ\) – прямоугольный и по теореме Пифагора \[(2-x)^2+(3\sqrt2-x\sqrt2)^2=(2+x)^2 \quad\Rightarrow\quad
\left[\begin{gathered}\begin{aligned} &x=9\\
&x=1 \end{aligned}\end{gathered}\right.\] Заметим, что \(x\) не может быть равен \(9\) (так как такой шар не может находиться внутри квадрата с ребром, равным \(5\)). Следовательно, \(x=1\).
2) Пусть второй шар касается верхнего основания. В этом случае все вычисляется аналогично первому случаю, картинка выглядит так:
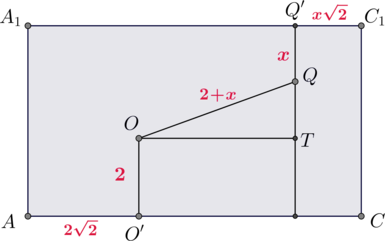
Получаем уравнение \[(2+x)^2=(3\sqrt2-x\sqrt2)^2+(3-x)^2\quad\Rightarrow\quad
\left[\begin{gathered}\begin{aligned} &x=\dfrac{11+5\sqrt3}2\\[2ex]
&x=\dfrac{11-5\sqrt3}2 \end{aligned}\end{gathered}\right.\] Также заметим, что подходит только \(x=\dfrac{11-5\sqrt3}2\).
Ответ:
\(1\) или \(\dfrac{11-5\sqrt3}2\)
Решите систему неравенств \[\begin{cases} 2x^2+4xy+11y^2\leqslant 1\\ 4x+7y\geqslant 3 \end{cases}\]
Заметим, что \(2x^2+4xy+11y^2=2(x^2+2xy+y^2)+9y^2=2(x+y)^2+9y^2\). Пусть \(\sqrt2(x+y)=t\), \(3y=z\). Тогда система примет вид: \[\begin{cases}
t^2+z^2\leqslant 1\\
2\sqrt2t+z\geqslant 3 \end{cases}\] Первое неравенство задает круг радиуса \(1\) с центром в \((0;0)\). Второе неравенство задает область, находящуюся выше прямой \(z=3-2\sqrt2t\):
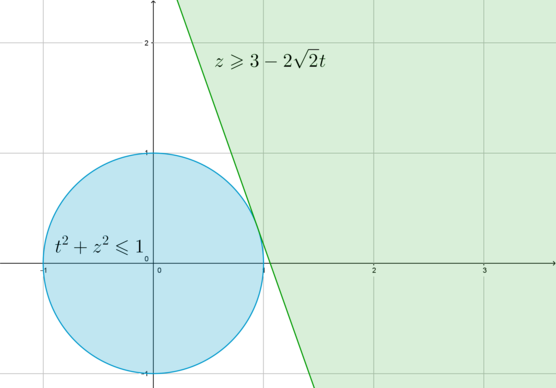
Найдем точки пересечения прямой \(z=3-2\sqrt2t\) с окружностью \(t^2+z^2=1\): \[t^2+(3-2\sqrt2t)^2=1\quad\Rightarrow\quad 9t^2-12\sqrt2t+8=0\] Дискриминант равен \(D=(12\sqrt2)^2-4\cdot 8\cdot 9=0\), следовательно, уравнение имеет один корень \[t=\dfrac{2\sqrt2}3\] То есть прямая и окружность имеют только одну точку пересечения, значит, прямая касается окружности. Следовательно, решением системы будет только эта точка (так как синяя область пересекается с зеленой областью по этой точке).
Таким образом, \[z=3-2\sqrt2\cdot \dfrac{2\sqrt2}3=\dfrac13\] Следовательно, \[\begin{cases}
t=\sqrt2(x+y)=\dfrac{2\sqrt2}3\\[2ex]
z=3y=\dfrac13 \end{cases} \quad\Rightarrow\quad \begin{cases}
x=\dfrac59\\[2ex]
y=\dfrac19 \end{cases}\]
Ответ:
\(x=\dfrac59 ; y=\dfrac19\)