Уровень Максим Олегович. Тренировочный вариант №1

Пусть \(c^\circ C = n^\circ N\). Так как зависимость линейная, то \(n = k\cdot c + a\), где \(k, \ a\) – неизвестные коэффициенты. Тогда \(c^\circ C = (k\cdot c + a)^\circ N\).

Так как \(0^\circ C = 0^\circ N\), то при \(c = 0\) должно быть \(n = 0\), откуда \(a = 0\).

Так как \(100^\circ C = 33^\circ N\), то при \(c = 100\) должно быть \(n = 33\), откуда \(k = \dfrac{33}{100}\). В итоге \(n = \dfrac{33}{100}c\), откуда находим, что при \(c = -273\): \(n = \dfrac{33}{100}\cdot(-273) = -90,09\). После округления получим \(-90\).

Ответ: -90

Для данного газа давление возрастает с ростом температуры, следовательно, необходимо найти на временном отрезке от \(3\) до \(4\) минут наименьшее значение температуры. Это значение достигается через \(3\) минуты после начала нагревания и равно \(35 C^0\). При этом давление станет \(0,4 \cdot 35 = 14\, Па\).

Ответ: 14

Средняя линия трапеции равна полусумме оснований. Полусумма оснований трапеции \(ABCD\) составляет \(0,8\) одного из оснований, тогда сумма оснований трапеции \(ABCD\) составляет \(2\cdot 0,8 = 1,6\) этого основания, обозначим его за \(AD\). Тогда \(BC + AD = 1,6AD\), откуда \(BC = 0,6AD\). Средняя линия равна \(0,8AD\), тогда отношение длины основания \(BC\) к длине средней линии равно \(0,6 : 0,8 = 0,75\).

Ответ: 0,75

Условие того, что выпало не менее \(9\) орлов эквивалентно тому, что выпало не более \(1\) решки, то есть либо ровно \(1\) решка, либо \(0\) решек.

Количество всевозможных различных исходов в серии из \(10\) испытаний равно \(2^{10} = 1024\).

Среди них есть \(11\) исходов, подходящих под условие: (Орёл; Орёл; ...; Орёл), (Орёл; Орёл; ...; Орёл; Решка), (Орёл; Орёл; ...; Решка; Орёл), ..., (Решка; Орёл; ...; Орёл), следовательно, искомая вероятность равна \[\dfrac{11}{1024}.\] После округления получим \(0,011\).

Ответ: 0,011

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

Решение уравнения \(\sin x = a\) имеет вид: \(x_1 = \mathrm{arcsin}\, a + 2\pi n, \ x_2 = \pi - \mathrm{arcsin}\, a + 2\pi n, n \in \mathbb{Z}\), откуда для исходного уравнения получаем \[\dfrac{\pi\sqrt{\pi}}{22} x_1 = \dfrac{-0,1\pi\sqrt{\pi}}{22} + 2\pi n, n \in \mathbb{Z}, \qquad\dfrac{\pi\sqrt{\pi}}{22} x_2 = \pi - \dfrac{-0,1\pi\sqrt{\pi}}{22} + 2\pi n, n \in \mathbb{Z},\] что равносильно \[x_1 = -0,1 + \dfrac{44}{\sqrt{\pi}} n, n \in \mathbb{Z},\qquad x_2 = \dfrac{22}{\sqrt{\pi}} + 0,1 + \dfrac{44}{\sqrt{\pi}} n, n \in \mathbb{Z}\] – подходят по ОДЗ. Среди корней наибольший не положительный \(x = -0,1\).

Ответ: -0,1

\[P = \dfrac{10}{2\sqrt{3} - \sqrt{2}} = \dfrac{(2\sqrt{3} + \sqrt{2})(2\sqrt{3} - \sqrt{2})}{2\sqrt{3} - \sqrt{2}} = 2\sqrt{3} + \sqrt{2}.\] По формуле Герона \(S_{\triangle ABC} = \sqrt{p(p - AB)(p - BC)(p - AC)}\), где \(p\) – полупериметр треугольника \(ABC\), \(p = \sqrt{3} + 0,5\sqrt{2}\), тогда \[S_{\triangle ABC}^2 = p(p - AB)(p - BC)(p - AC) \qquad\Rightarrow\]

\[\Rightarrow \qquad\dfrac{S_{\triangle ABC}^2}{p(p - AB)} = (p - BC)(p - AC) = p^2 - p(AC + BC) + AC\cdot BC,\] откуда

\(\begin{multline*} \dfrac{1,25}{(\sqrt{3} + 0,5\sqrt{2})\cdot 0,5\sqrt{2}} = 3,5 + \sqrt{6} - (\sqrt{3} + 0,5\sqrt{2})(AC + BC) + \sqrt{6},\\[4pt] AC + BC = \dfrac{3,5 + 2\sqrt{6}}{\sqrt{3} + 0,5\sqrt{2}} - \dfrac{2,5}{(\sqrt{3} + 0,5\sqrt{2})^2\cdot\sqrt{2}} =\\[4pt] = \dfrac{(3,5 + 2\sqrt{6})(\sqrt{3} + 0,5\sqrt{2})\sqrt{2}}{(\sqrt{3} + 0,5\sqrt{2})^2\sqrt{2}} - \dfrac{2,5}{(\sqrt{3} + 0,5\sqrt{2})^2\cdot\sqrt{2}} =\\[4pt] = \dfrac{(3,5 + 2\sqrt{6})(\sqrt{3} + 0,5\sqrt{2})\sqrt{2}}{(\sqrt{3} + 0,5\sqrt{2})^2\sqrt{2}} - \dfrac{2,5}{(\sqrt{3} + 0,5\sqrt{2})^2\cdot\sqrt{2}} = \dfrac{5,5\sqrt{6} + 13}{3,5\sqrt{2} + 2\sqrt{3}}.\\[4pt] (AC + BC)\cdot(\sqrt{3} - \sqrt{2}) = \dfrac{(5,5\sqrt{6} + 13)(\sqrt{3} - \sqrt{2})}{3,5\sqrt{2} + 2\sqrt{3}} = \dfrac{3,5\sqrt{2} + 2\sqrt{3}}{3,5\sqrt{2} + 2\sqrt{3}} = 1 \end{multline*}\)

Ответ: 1

По определению первообразной \(f(x) = F'(x)\), тогда уравнение \(f(x) = 0\) равносильно \(F'(x) = 0\). Производная функции равна \(0\) в точности в тех точках, где касательная к её графику параллельна оси \(Ox\).

По рисунку видно, что на отрезке \([2,5; 5,5]\) касательная к графику \(y = F(x)\) параллельна оси \(Ox\) в \(2\) точках (в точках с абсциссами \(x = 4\), \(x = 5\)).

Ответ: 2

Обозначим \(AA_1 = a\), \(A_1D_1 = b\), \(D_1C_1 = c\), тогда площадь полной поверхности \(ABCDA_1B_1C_1D_1\) равна \[S_{\text{полн}} = 2ab + 2ac + 2bc.\] Площадь квадрата со стороной \(a + b + c\) равна \((a + b + c)^2\), сумма площадей квадратов со сторонами \(a\), \(b\), \(c\) равна \(a^2 + b^2 + c^2\), тогда искомая величина равна

\[\begin{aligned} (a + b + c)^2 - (a^2 + b^2 + c^2) &= a^2 + b^2 + c^2 + 2ab + 2ac + 2bc - (a^2 + b^2 + c^2) =\\ &= 2ab + 2ac + 2bc = S_{\text{полн}} = 12. \end{aligned}\]

Ответ: 12

Используя формулу приведения \(\sin(90^\circ \pm \alpha) = \cos \alpha\), исходное выражение можно преобразовать следующим образом: \[\dfrac{15\cos{\sqrt{5}^\circ}}{\sin{(-\sqrt{5}^\circ + 90^\circ)}} = \dfrac{15\cos{\sqrt{5}^\circ}}{\sin{(90^{\circ} -\sqrt{5}^\circ)}} = \dfrac{15\cos{\sqrt{5}^\circ}}{\cos{\sqrt{5}^\circ}} = 15.\]

Ответ: 15

Количество лет, через которое масса изотопа станет не более, чем \(25\, мг\), удовлетворяет соотношению \[m_0\cdot 2^{-\frac{t}{T}} = m(t) \leqslant 25,\] откуда \[100\cdot 2^{-\frac{t}{400}} \leqslant 25\ \Leftrightarrow\ 2^{-\frac{t}{400}} \leqslant \dfrac{1}{4}\ \Leftrightarrow\ 2^{-\frac{t}{400}} \leqslant 2^{-2}\ \Leftrightarrow\ -\dfrac{t}{400} \leqslant -2\ \Leftrightarrow\ \dfrac{t}{400} \geqslant 2,\] откуда \(t \geqslant 800\), то есть минимум через \(800\) лет масса изотопа станет не более, чем \(25\, мг\).

Ответ: 800

Последовательность количеств бабочек, пойманных за первый, второй и т.д. дни соответственно, представляет собой арифметическую прогрессию, сумма первых \(15\) элементов которой равна \(120\).

Формула для суммы первых \(n\) членов арифметической прогрессии:

\[S_n = \dfrac{a_1 + a_n}{2}n,\] где \(a_1, \ a_n\) – первый и \(n\)-ый члены арифметической прогрессии соответственно. При этом по условию \(n = 15, \ S_{15} = 120\), откуда находим \(a_1 + a_{15} = 16\).

Так как в первый день Света поймала \(1\) бабочку, то \(a_1 = 1\), следовательно, \(a_{15} = 15\).

При этом \(a_{15} = 14d + a_1\), где \(d\) – разница в количествах бабочек, пойманных Светой во второй и первый дни, откуда находим \(d = 1\). В восьмой день она поймала \(1 + 7\cdot 1 = 8\) бабочек.

Ответ: 8

ОДЗ: \(x \neq -1\). Решим на ОДЗ:

1) \[y' = 13 \dfrac{(2x + 3)(x + 1) - (x^2 + 3x + 6)}{(x + 1)^2} = 13 \dfrac{x^2 + 2x - 3}{(x + 1)^2}.\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[13 \dfrac{x^2 + 2x - 3}{(x + 1)^2} = 0\qquad\Leftrightarrow\qquad x^2 + 2x - 3 = 0\] – на ОДЗ, откуда находим корни \(x_1 = 1,\ x_2 = -3\). Производная функции \(y\) не существует при \(x = -1\), но \(x = -1\) не входит в ОДЗ. Таким образом, \[y' = 13\dfrac{(x - 1)(x+3)}{(x+1)^2}.\] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Найдём промежутки знакопостоянства \(y'\) на рассматриваемом отрезке \([0; 12]\):



4) Эскиз графика на отрезке \([0; 12]\):



Таким образом, наибольшее на \([0; 12]\) значение функция достигает в \(x = 0\) или в \(x = 12\). Сравним эти значения:

\(y(0) = 13\cdot \dfrac{6}{1} = 78\),

\(y(12) = 13\cdot \dfrac{186}{13} = 186\).

Итого: \(186\) – наибольшее значение функции \(y\) на \([0; 12]\).

Ответ: 186

ОДЗ: \(x\) – произвольное.
По основному тригонометрическому тождеству:
\(2\cos^2x + 2\sin(2x) = 3\).
\(2\cos^2x + 2\sin(2x) = 3\sin^2x + 3\cos^2x\).
\(2\cos^2x + 4\sin x\cdot\cos x = 3\sin^2x + 3\cos^2x\).
\(-\cos^2x + 4\sin x\cdot\cos x - 3\sin^2x = 0\).
Проверим, что \(\cos x\neq 0\): если \(\cos x = 0\), то \(-3\sin^2x = 0\), но в силу основного тригонометрического тождества \(\sin x\) и \(\cos x\) не могут быть равны 0 одновременно.
Тогда на \(\cos^2x\) можно поделить:
\(-1 + 4\mathrm{tg}\, x - 3\mathrm{tg}^2\, x = 0\).
Сделаем замену: \(t = \mathrm{tg}\, x\)
\(-1 + 4t - 3t^2 = 0\).
\(t_1 = 1\), \(t_2 = \dfrac{1}{3}\).
\(\mathrm{tg}\, x = 1\), \(\mathrm{tg}\, x = \dfrac{1}{3}\).
1) \(\mathrm{tg}\, x = 1\), откуда \(x = \dfrac{\pi}{4} + \pi k, k\in\mathbb{Z}\).
2) \(\mathrm{tg}\, x = \dfrac{1}{3}\), откуда \(x = \mathrm{arctg}\,\dfrac{1}{3} + \pi n, n\in\mathbb{Z}\).
Окончательно: \(x = \dfrac{\pi}{4} + \pi k, k\in\mathbb{Z}\), \(x = \mathrm{arctg}\,\dfrac{1}{3} + \pi n, n\in\mathbb{Z}\).

б) Рассмотрим сначала \(-\dfrac{3\pi}{2} \leqslant \dfrac{\pi}{4} + \pi k \leqslant \dfrac{\pi}{2}\), что равносильно \(-\dfrac{7}{4} \leqslant k \leqslant \dfrac{1}{4}\), то есть подходят \(x\) при \(k = -1\) и \(k = 0\): \(x = -\dfrac{3\pi}{4}\), \(x = \dfrac{\pi}{4}\).

Рассмотрим наконец \(-\dfrac{3\pi}{2} \leqslant \mathrm{arctg}\, \dfrac{1}{3} + \pi n \leqslant \dfrac{\pi}{2}\). Так как \(0 < \dfrac{1}{3} < \dfrac{1}{\sqrt{3}}\), то \(\mathrm{arctg}\, 0< \mathrm{arctg}\,\dfrac{1}{3} < \mathrm{arctg}\,\dfrac{1}{\sqrt{3}}\), откуда \(0 < \mathrm{arctg}\,\dfrac{1}{3} < \dfrac{\pi}{6}\). Таким образом, \(0 < \dfrac{\mathrm{arctg}\,\frac{1}{3}}{\pi} < \dfrac{1}{6}\). Обозначим \(\dfrac{\mathrm{arctg}\,\frac{1}{3}}{\pi} = A\).
Теперь \(-\dfrac{3}{2} - A \leqslant n \leqslant \dfrac{1}{2} - A\), то есть подходят \(x\) при \(n = -1\) и \(n = 0\): \(x = \mathrm{arctg}\,\dfrac{1}{3} - \pi\) и \(x = \mathrm{arctg}\,\dfrac{1}{3}\).

Ответ:

а) \(\dfrac{\pi}{4} + \pi k, k\in\mathbb{Z}\), \(\mathrm{arctg}\, \dfrac{1}{3} + \pi n, n\in\mathbb{Z}\).

б) \(-\dfrac{3\pi}{4}\), \(\dfrac{\pi}{4}\), \(\mathrm{arctg}\, \dfrac{1}{3} - \pi\), \(\mathrm{arctg}\,\dfrac{1}{3}\).

а) По условию \(ABCD\) представляет собой правильную треугольную пирамиду, все ребра которой равны \(24\). Построим сечение пирамиды плоскостью \(MNK\). Продлим прямую \(NK\) до пересечения с прямой \(AC\) – получим точку \(Q\). Соединив точки \(Q\) и \(M\), получим линию пересечения основания – отрезок \(MT\). Таким образом, сечением является четырехугольник \(MNKT\).

б) Проведем \(LH\perp MNK\) и \(LS\perp MT\). По теореме о трех перпендикулярах \(HS\perp MT\). Тогда \(\triangle LHS\) – прямоугольный, причем \(\angle LSH\) и есть угол между плоскостями \(MNK\) и \(ABC\). Таким образом, т.к. \(\angle LSH=30^\circ \Rightarrow LH=\dfrac{1}{2}LS\). Найдем \(LS\).

По теореме Менелая для \(\triangle ADC\) и прямой \(QK\) имеем:

\(\dfrac{AN}{ND}\cdot \dfrac{DK}{KC}\cdot \dfrac{CQ}{QA}=1 \Rightarrow QA=8\)

Т.к. \(QA=AM\) и \(\angle CAB=60^\circ \Rightarrow \angle AQM=30^\circ \Rightarrow LS=\dfrac{1}{2}QL=10 \Rightarrow LH=5\).

Ответ:

б) \(5\).

ОДЗ:

\[\begin{aligned} \begin{cases} x^2 + 1 > 0\\ 4x > 0\\ 3^x - 2\neq 0\\ x > 0\\ x\neq 1 \end{cases} \qquad\Leftrightarrow\qquad \begin{cases} x\neq \log_3 2\\ x > 0\\ x\neq 1 \end{cases} \end{aligned}\]

На ОДЗ \(x^2 + 1 > 1\), следовательно, \(\ln(x^2 + 1) > 0\), тогда исходное неравенство на ОДЗ равносильно

\[\begin{aligned} \dfrac{\log_2^2 4x + \log_2 4x - \log_2 4}{(3^x - 2)\ln x}\leqslant 0 \end{aligned}\]

Найдём нули числителя:

\[\begin{aligned} \log_2^2 4x + \log_2 4x - \log_2 4 = 0 \end{aligned}\]

Сделаем замену \(\log_2 4x = t\):

\[\begin{aligned} t^2 + t - 2 = 0\qquad\Leftrightarrow\qquad t = \dfrac{-1\pm 3}{2} \end{aligned}\]

\(\bullet\) \(\log_2 4x = -2\qquad\Leftrightarrow\qquad\log_2 4x = \log_2 0,25\qquad\Leftrightarrow\qquad 4x = 0,25\qquad\Leftrightarrow\qquad x = \dfrac{1}{16}\)
\(\bullet\) \(\log_2 4x = 1\qquad\Leftrightarrow\qquad\log_2 4x = \log_2 2\qquad\Leftrightarrow\qquad 4x = 2\qquad\Leftrightarrow\qquad x = \dfrac{1}{2}\)

Найдём нули знаменателя:
1) \[3^x - 2 = 0\qquad\Leftrightarrow\qquad 3^x = 3^{\log_3 2}\qquad\Leftrightarrow\qquad x = \log_3 2\] 2) \[\ln x = 0\qquad\Leftrightarrow\qquad\ln x = \ln 1\qquad\Leftrightarrow\qquad x = 1\]

По методу интервалов:



откуда \(x\in\left[\dfrac{1}{16}; \dfrac{1}{2}\right]\cup(\log_3 2 ; 1)\)
пересечём ответ с ОДЗ: \[x\in\left[\dfrac{1}{16}; \dfrac{1}{2}\right]\cup(\log_3 2 ; 1)\,.\]

Ответ:

\(\left[0,0625; 0,5\right]\cup(\log_3 2 ; 1)\)

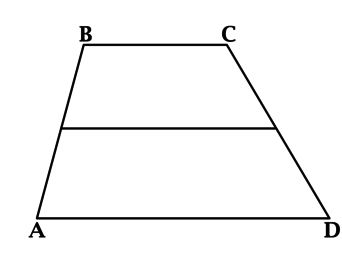
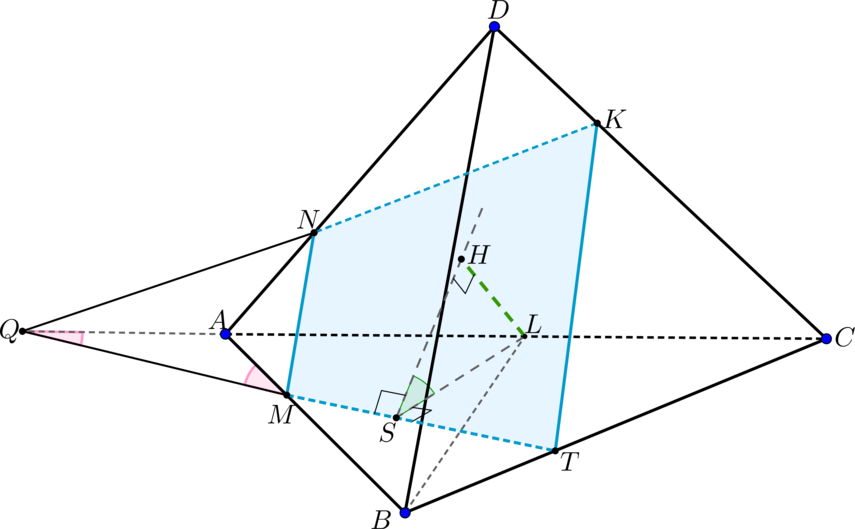
а) Пусть \(M\) и \(N\) – середины \(AB\) и \(CD\) соответственно, \(K\) – точка пересечения серединных перпендикуляров к сторонам \(AB\) и \(CD\).

Из точки \(A\) на прямую, содержащую \(CD\), опустим перпендикуляр \(AC'\). Из точки \(D\) на прямую, содержащую \(AB\), опустим перпендикуляр \(DB'\).

Так как \(\angle A = \angle D\), то треугольники \(AB'D\) и \(AC'D\) равны по гипотенузе и острому углу, откуда \(C'D = AB'\). Обозначим \(C'D = h\). Возможны 2 случая:

1) отрезок \(BC\) пересекает \(B'C'\),

2) отрезок \(BC\) не пересекает \(B'C'\).

1) Пусть \(BB' = a\), \(CC' = b\) и \(AB' > AB\), тогда \(C'D < CD\).
\(AB = h - a\), \(CD = h + b\), откуда \[AM = \dfrac{h - a}{2},\qquad DN = \dfrac{h + b}{2}.\]

Треугольники \(AMK\) и \(AB'D\) подобны по двум углам, откуда \[\dfrac{h - a}{2h} = \dfrac{AK}{AD}\qquad\Rightarrow\qquad AK = \dfrac{h - a}{2h}AD.\]

Аналогично из подобия треугольников \(KND\) и \(AC'D\) получаем \(DK = \dfrac{h + b}{2h}AD\).

Так как \(AK + KD = AD\), то \[AD = \dfrac{h - a}{2h}AD + \dfrac{h + b}{2h}AD,\] откуда \[-a + b = 0\qquad\Rightarrow\qquad a = b.\]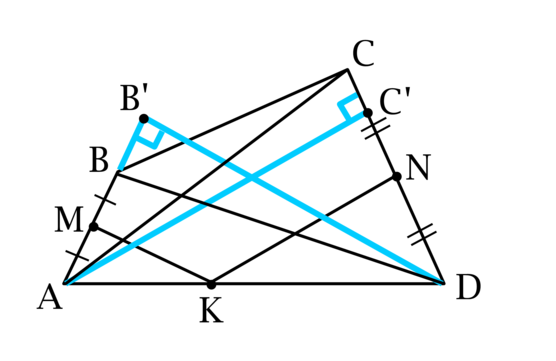

Так как треугольники \(AB'D\) и \(AC'D\) равны (по гипотенузе и острому углу), то \(B'D = A'C\). Так как \(BB' = CC'\), то прямоугольные треугольники \(BB'D\) и \(ACC'\) равны (по двум катетам), следовательно, \(AC = BD\).

2) Аналогично первому случаю, только в итоге получим \[AD = \dfrac{h - a}{2h}AD + \dfrac{h - b}{2h}AD\] или \[AD = \dfrac{h + a}{2h}AD + \dfrac{h + b}{2h}AD.\] В обоих этих случаях будет \(a + b = 0\), откуда в силу \(a\geqslant 0\), \(b\geqslant 0\) получим, что \(a = b = 0\), но \(BD' = AC'\) (так как треугольники \(AB'D\) и \(AC'D\) равны).

В итоге \(AC = BD\), тогда из теоремы о биссектрисе (биссектриса треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам) получаем нужное равенство.

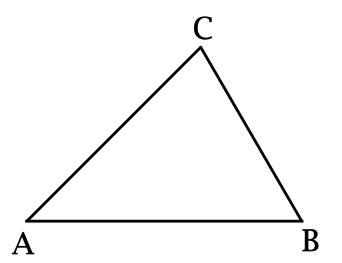
б) Так как у треугольников \(BDA\) и \(CDA\) основание \(AD\) – общее, то \[\dfrac{\rho(B; AD)}{\rho(C; AD)} = \dfrac{S_{\triangle BDA}}{S_{\triangle CDA}}.\]

Так как \(AC = BD\), а \(AD\) общая для треугольников \(BDA\) и \(CDA\), то \[\dfrac{S_{\triangle BDA}}{S_{\triangle CDA}} = \dfrac{\sin\alpha}{\sin\beta}.\] В итоге \[\dfrac{\rho(B; AD)}{\rho(C; AD)} = \dfrac{\sin\alpha}{\sin\beta}.\]

Ответ:

б) \(\dfrac{\sin\alpha}{\sin\beta}\).

Составим таблицу, обозначив за \(t=\dfrac{100+y}{100}\): \[\begin{array}{|l|c|c|} \hline \text{Год} & \text{Сумма на счете до} & \text{Сумма на счете после}\\ &\text{начисления }\%\text{(февраль)} & \text{начисления }\%\text{(декабрь)}\\ \hline 2015 & A & tA\\ \hline 2016 & tA & t^2A\\ \hline 2017 & t^2A-A & t(t^2A-A)\\ \hline 2018 & t(t^2A-A)-2A & t(t(t^2A-A)-2A)\\ \hline 2019 & t(t(t^2A-A)-2A)-A &\\ \hline \end{array}\]

Для того, чтобы Дмитрию удалось сделать то, что он задумал, нужно:
\[\begin{cases} \begin{aligned} & t^2A-A \geqslant 0\\ & t(t^2A-A)-2A \geqslant0\\ & t(t(t^2A-A)-2A)-A \geqslant0 \end{aligned} \end{cases}\]

(т.к. он не может снять со счета больше, чем есть на счете в данный момент)

Заметим, что, т.к. \(t>1 \Rightarrow A(t^2-1) \geqslant0\) при всех \(t\).
Рассмотрим другие два неравенства:
\[\begin{cases} \begin{aligned} & t^3-t-2 \geqslant0\\ & t^4-t^2-2t-1 \geqslant0 \end{aligned} \end{cases}\]
Заметим, что если выполнено \(t^4-t^2-2t-1 \geqslant0\), то \(t^3-t-2 \geqslant \dfrac{1}{t}>0\), т.к. \(t>1\). Т.е. при тех значениях \(t\), при которых выполнено второе неравенство, выполнено и первое неравенство. Значит, решим только второе неравенство:
\[t^4-(t+1)^2 \geqslant0 \Rightarrow (t^2-t-1)(t^2+t+1) \geqslant0 \Rightarrow t \geqslant \dfrac{1+\sqrt5}{2}\]
Сделав обратную замену, получим: \(y\geqslant 50(\sqrt5-1)\). Выполнив оценку числа в правой части, получим наименьшее целое \(y=62 \%\).

Ответ:

\(62 \%\).

Рассмотрим множество функций \(f_a(x)=x^2-(a^2-2a-3)x+a^2+2\). При каждом фиксированном \(a\) это квадратичная функция, графиком которой является парабола с ветвями, направленными вверх, которая может выглядеть как \((1)\) (\(D=0\)), \((2)\) (\(D>0\)) или \((3)\) (\(D<0\)):

Для того, чтобы решением неравенства являлся отрезок \([2;3]\), необходимо, чтобы парабола выглядела как \((2)\), то есть необходимо выполнение следующих условий:

\(\begin{cases} (a^2-2a-3)^2-4(a^2+2)>0\\ f_a(2)=0\\ f_a(3)=0 \end{cases} \quad \Rightarrow \quad \begin{cases} (a^2-2a-3)^2-4(a^2+2)>0\\ a^2-4a-12=0\\ a^2-3a-10=0 \end{cases} \quad \Rightarrow \)

\(\Rightarrow \quad \begin{cases} (a^2-2a-3)^2-4(a^2+2)>0\\ a=-2 \end{cases}\)

Заметим, что при \(a=-2\) неравенство \((a^2-2a-3)^2-4(a^2+2)>0\) выполняется, т.к. оно равносильно \(1>0\). Следовательно, \(a\in \{-2\}\).

Ответ:

\(a\in \{-2\}\)

Пусть НОД\((18n+1,45n+1)=a\), тогда по определению наибольшего общего делителя \((18n+1)\, \vdots \, a\) и \((45n+1)\, \vdots \,a\), но тогда \(\bigl(5(18n+1)-2(45n+1)\bigr)\, \vdots \,a\).

Так как \(5(18n+1)-2(45n+1)=90n+5-90n-2=3\), то \(3\, \vdots \, a\), значит, \(a\) равно либо \(1\), либо \(3\).

Но так как \(18n+1\) не делится на \(3\), то \(a=1\), следовательно, НОД\((18n+1,45n+1)=1\).

Таким образом, дробь \(\dfrac{18n+1}{45n+1}\) – несократима.

Ответ:

Доказательство