Боря выписал все различные делители числа \(12\). Сколько чисел выписал Боря?
Различные делители числа \(12\) – это \(1\), \(2\), \(3\), \(4\), \(6\), \(12\), то есть 6 чисел.
Ответ:
\(6\)
19. Задачи на теорию чисел
Боря выписал все различные делители числа \(12\). Сколько чисел выписал Боря?
Различные делители числа \(12\) – это \(1\), \(2\), \(3\), \(4\), \(6\), \(12\), то есть 6 чисел.
Ответ:
\(6\)
Шесть пчёлок прилетели опылять два разных цветочка. Они договорились, что один цветочек будет опылять ровно одна пчёлка. Им предстоит решить, кому достанутся эти два цветочка на опыление. Сколькими способами они могут распределить двух пчёлок по двум разным цветочкам?
На первый цветочек может претендовать любая из 6 пчёлок. Как только выбрана пчёлка, которая будет опылять первый цветочек, на второй цветочек может претендовать любая из 5 оставшихся пчёлок.
Какую бы пчёлку не назначили на первый цветочек, после этого назначения остаётся 5 различных возможных вариантов назначить пчёлку на второй цветочек. То есть каждый из 6 вариантов для первого цветочка даёт 5 различных вариантов для второго цветочка.
Получаем, что всего вариантов – “шесть раз по пять”\( \), то есть \(6\cdot 5 = 30\).
Ответ:
\(30\)
Боря выписал все различные делители числа \(120\). Сколько чисел выписал Боря?
Разложим \(120\) на простые множители: \(120 = 2^3\cdot 3\cdot 5\). Все делители числа \(120\) равны \(2^a\cdot 3^b\cdot 5^c\), где
\(a\) может принимать значения \(0, 1, 2\) или \(3\),
\(b\) может принимать значения \(0\) или \(1\),
\(c\) может принимать значения \(0\) или \(1\).
При этом если тройки \((a_1, b_1, c_1)\) и \((a_2, b_2, c_2)\) не совпадают, то числа \(2^{a_1}\cdot 3^{b_1}\cdot 5^{c_1}\) и \(2^{a_2}\cdot 3^{b_2}\cdot 5^{c_2}\) – различны.
Таким образом, у числа \(120\) столько же различных делителей, сколько существует различных троек вида \((a, b, c)\), где \(a\) принимает одно из четырёх значений, \(b\) принимает одно из двух значений, \(c\) принимает одно из двух значений, то есть количество подходящих троек равно \(4\cdot 2\cdot 2 = 16\).
Ответ:
\(16\)
В честь своего дня рождения Тимур накрыл праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей, ведь у него имеется шесть разных гостевых стульев (которые уже стоят у стола и двигать их он не намерен). Сколькими способами он может это сделать?
Так как место Тимура за столом фиксировано, то можно считать, что его за столом не будет (ответ от этого не изменится).
Пусть Тимур как-то занумеровал стулья. Тогда на первый стул может претендовать любой из 6 гостей.
Какой бы из 6 гостей не занял первый стул, на второй стул может претендовать любой из оставшихся на этот момент 5 гостей. \[\dots\]
На последний шестой стул будет претендовать один единственный гость.
В итоге: каждый из 6 вариантов для первого стула даёт пять различных вариантов для второго стула и т.д., то есть всего есть \(6! = 1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6 = 720\) различных способов рассадить гостей.
Ответ:
\(720\)
Боря выписал все различные делители числа \(2016\). Сколько чисел выписал Боря?
Разложим \(2016\) на простые множители: \(2016 = 2^5\cdot 3^2\cdot 7\). Все делители числа \(2016\) равны \(2^a\cdot 3^b\cdot 7^c\), где
\(a\) может принимать значения \(0, 1, 2\), \(3\), \(4\) или \(5\),
\(b\) может принимать значения \(0\), \(1\) или \(2\),
\(c\) может принимать значения \(0\) или \(1\).
При этом если тройки \((a_1, b_1, c_1)\) и \((a_2, b_2, c_2)\) не совпадают, то числа \(2^{a_1}\cdot 3^{b_1}\cdot 7^{c_1}\) и \(2^{a_2}\cdot 3^{b_2}\cdot 7^{c_2}\) – различны.
Таким образом, у числа \(2016\) столько же различных делителей, сколько существует различных троек вида \((a, b, c)\), где \(a\) принимает одно из шести значений, \(b\) принимает одно из трёх значений, \(c\) принимает одно из двух значений, то есть количество подходящих троек равно \(6\cdot 3\cdot 2 = 36\).
Ответ:
\(36\)
В честь своего следующего дня рождения Тимур планирует накрыть праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей на шесть одинаковых гостевых стульев (ему не важно, на какой гостевой стул кто сядет, важно лишь кто будет соседями каждого гостя). Сколькими способами он может это сделать?
Справа от Тимура может сесть любой из 6 гостей. После того, как Тимур определится со своим правым соседом, на место справа от правого соседа Тимура может сесть любой из 5 гостей и т.д.
В итоге сосед, сидящий слева от Тимура будет, определён однозначно, то есть имеется \(6! = 720\) вариантов, но не все они различны.
Пусть Тимур зафиксировал гостя, который будет его соседом справа, зафиксировал и его соседа справа и т.д. Он получил некоторую последовательность, в которой он будет сажать гостей, двигаясь в одну сторону вдоль граничной окружности стола.
Но если он будет сажать гостей в той же последовательности, двигаясь в другую сторону вдоль окружности, то при этом для каждого гостя состав его соседей не изменится.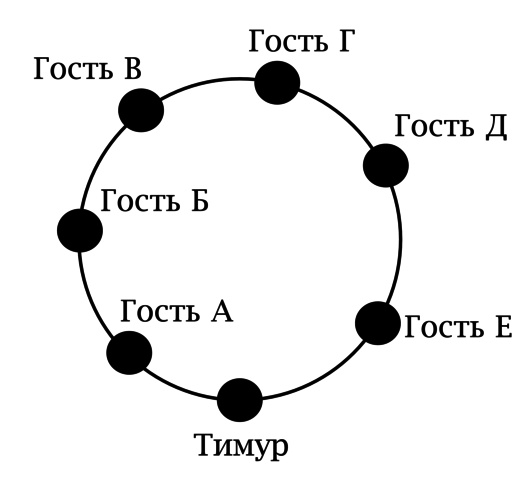
Таким образом, когда мы получили \(6!\) вариантов, каждый вариант рассадки мы учли ровно по два раза, следовательно, у Тимура есть \(\dfrac{6!}{2} = 360\) способов рассадить гостей.
Ответ:
\(360\)
Белоснежка и семь гномов садятся за круглый стол. Известно, что Ворчун не хочет сидеть рядом с Весельчаком и Соней. Сколькими способами их можно рассадить за стол так, чтобы Ворчуна всё устраивало, если считать, что не важно, кто на какое место сядет, важно только, кто будет соседями каждого гнома и Белоснежки?
Ответ не зависит от того, в каком порядке мы будем сажать Белоснежку и гномов за стол. Пусть первым за стол садится всегда Ворчун. Тогда его правым соседом может быть один из 5 кандидатов. После того, как его правый сосед выбран, на роль левого соседа Ворчуна могут претендовать 4 кандидата.
Далее имеем ситуацию как на рисунке: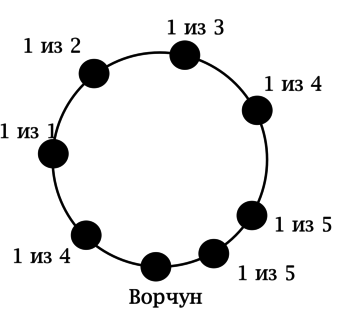
Таким образом, есть \(1\cdot 2\cdot 3\cdot 4\cdot 4\cdot 5\cdot 5 = 2400\) способов, но не все они различны. На самом деле каждый способ мы учли по два раза (если рассаживать кандидатов по часовой стрелке в определённой последовательности и если рассаживать их против часовой стрелки в той же последовательности, то рассадки будут одинаковыми).
В итоге есть \(2400 : 2 = 1200\) способов, которыми можно рассадить за стол гномов и Белоснежку так, чтобы Ворчуна всё устроило.
Ответ:
\(1200\)
При подготовке к сдаче Единого государственного экзамена по математике у большинства школьников возникают сложности с решением задач из раздела «Комбинаторика». Ученикам нелегко даются способы вычисления распределения элементов, поэтому стоит обратить на данную тему особое внимание.
Чтобы знать все необходимые формулы раздела «Комбинаторика» и быстро распределять элементы, воспользуйтесь нашим удобным онлайн-сервисом. На сайте вы найдете все необходимое для грамотной подготовки к ЕГЭ: правила, примеры с решениями и индивидуальные задания, которые постоянно обновляются и дополняются. Вся информация собрана преподавателями «Школково». Они систематизировали и изложили ее в максимально понятной форме, поэтому проблем даже с упражнениями сложного уровня у учеников не возникнет.
Мы предлагаем наиболее удобный метод повторения и усвоения информации по трудным тематикам. Для того, чтобы эффективно подготовиться к сдаче заключительного экзаменационного тестирования, рекомендуем начать с основ — легких задач по распределению элементов, постепенно переходя к сложным. Благодаря такому подходу каждый ученик сможет выявить для себя наиболее сложные типы упражнений и при подготовке уделить им больше времени.
Перед тем, как приступать к выполнению заданий, ознакомьтесь с формулами в разделе «Теоретическая справка». Потренируйтесь, решая типовые примеры, и переходите в раздел «Каталоги». В нем вы найдете большое количество упражнений различного уровня сложности и сможете выбрать подходящие для вас варианты.
При возникновении трудностей выпускник может отложить решение задачи по комбинаторике, добавив ее в «Избранное». Позже к ней можно вернуться для повторного изучения самостоятельно или уже с помощью преподавателя.
Если вы понимаете, что задания легкого и среднего уровня даются вам без проблем, смело пропускайте их и переходите к сложным упражнениям.
Начните готовиться к Единому государственному экзамену уже сейчас на портале «Школково»! Уделяйте достаточное количество времени выполнению заданий на нашем сайте, и результат не заставит себя ждать. С нашей помощью в скором времени вы сможете выполнять упражнения на сочетание чисел, с которыми ранее не справлялись.
Занятия на портале «Школково» совершенно бесплатны. Онлайн-сервисом могут пользоваться не только школьники из Москвы, но и других городов России. Просто зарегистрируйтесь на сайте для сохранения личных достижений и начинайте занятия! Желаем успехов в подготовке к ЕГЭ!