Задачам, в которых требуется построить сечение фигур плоскостью, отводится достаточно большое количество времени в рамках базового школьного курса геометрии. Подобные упражнения позволяют учащимся лучше усвоить базовые аксиомы стереометрии и систематизировать имеющиеся знания. Однако, как показывает опыт предыдущих лет, задачи, в которых требуется построить сечение фигуры плоскостью, вызывают у выпускников определенные сложности. При этом уметь справляться с ними должны все учащиеся, независимо от уровня подготовки.
Основные нюансы
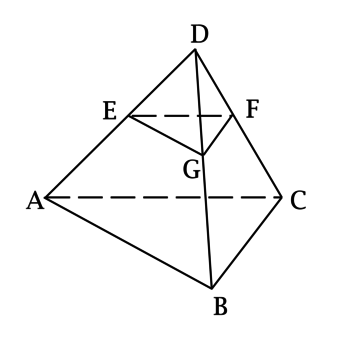
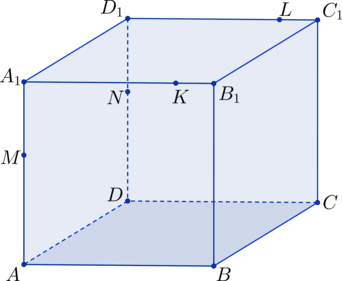
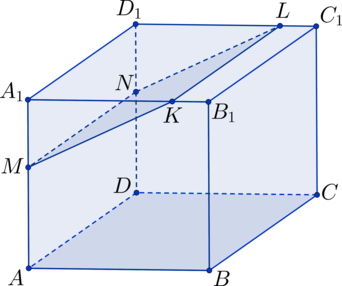
Сечение многогранника представляет собой многоугольник. Его вершины есть точки пересечения секущей плоскости с ребрами многоугольника. А стороны — это линии пересечения секущей плоскости с гранями.
Для того чтобы построить прямую пересечения двух плоскостей, необходимо найти их общие точки и провести через них прямую. Это утверждение подтверждается двумя аксиомами:
- Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит ей.
- Если плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку.
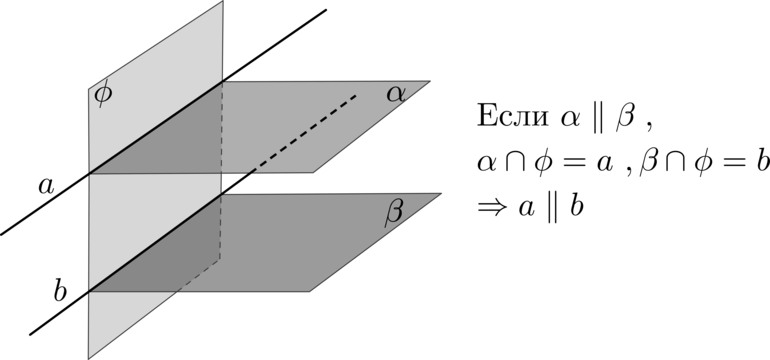
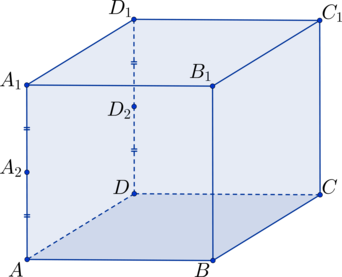
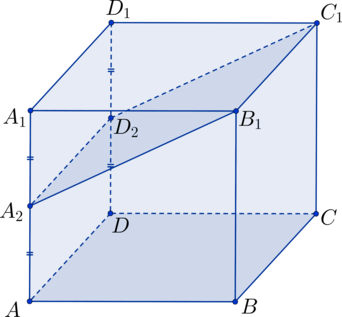
Построение пространственных сечений объемных геометрических фигур можно осуществлять на основании двух приведенных выше стереометрических аксиом, а также теорем о параллельности прямых и плоскостей.
Занимайтесь вместе с математическим порталом «Школково» для качественной подготовки к экзамену!
С необходимостью поиска подходящей информации сталкиваются многие учащиеся. Далеко не всегда учебник есть под рукой в нужный момент. А подходящие формулы для расчета площади сечения пирамиды, куба и других геометрических фигур в задачах ЕГЭ оказывается непросто даже в Интернете в онлайн-режиме.
Образовательный проект «Школково» поможет качественно подготовиться к прохождению аттестационного испытания. Наш портал предлагает преподавателям и старшеклассникам выстроить алгоритм занятия по-новому, переходя от простого к сложному. Мы убеждены, что именно такой подход позволит выпускникам определить темы, которые нуждаются в более детальном изучении.
Базовая информация, которую необходимо знать для выполнения заданий ЕГЭ на построение сечения фигур, представлена в разделе «Теоретическая справка». Изучив материал, подготовленный нашими специалистами, школьники смогут восполнить пробелы в знаниях без помощи репетитора.
Чтобы задачи на построение сечений фигур или, например, на комбинированные поверхности не вызывали затруднений, мы предлагаем также попрактиковаться в выполнении упражнений. Большая подборка заданий представлена в разделе «Каталог». Выполнять их школьники могут в онлайн-режиме, находясь в любом российском городе.