Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
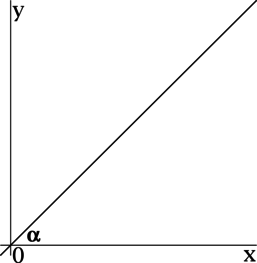
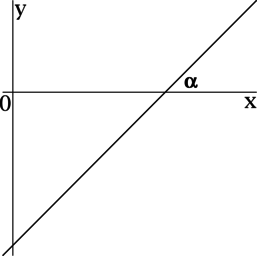
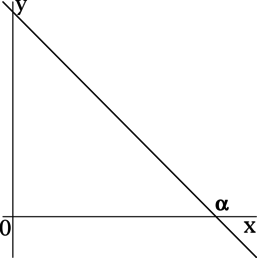
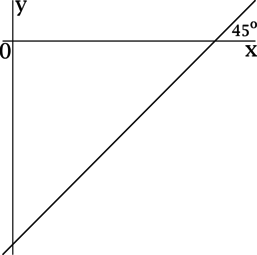
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.