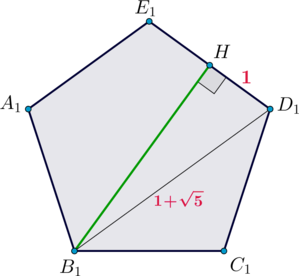
\(\blacktriangleright\) Угол между прямыми – это острый или прямой угол.
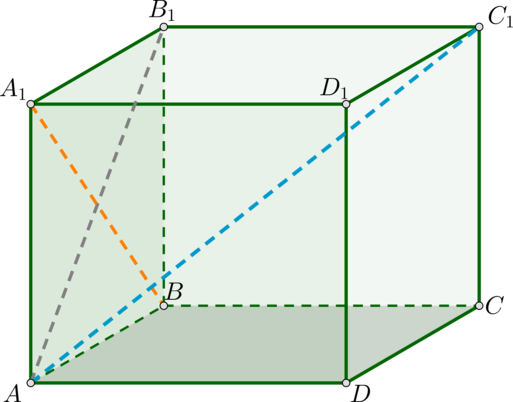
\(\blacktriangleright\) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
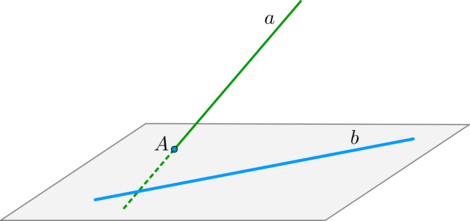
\(\blacktriangleright\) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых \(a\) провести плоскость, параллельную второй прямой \(b\) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую \(c\), параллельную прямой \(b\);
Шаг 3: тогда угол между прямыми \(a\) и \(b\) будет равен углу между прямыми \(a\) и \(c\).
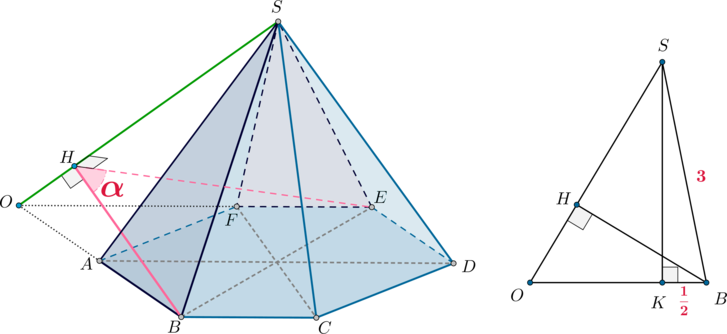
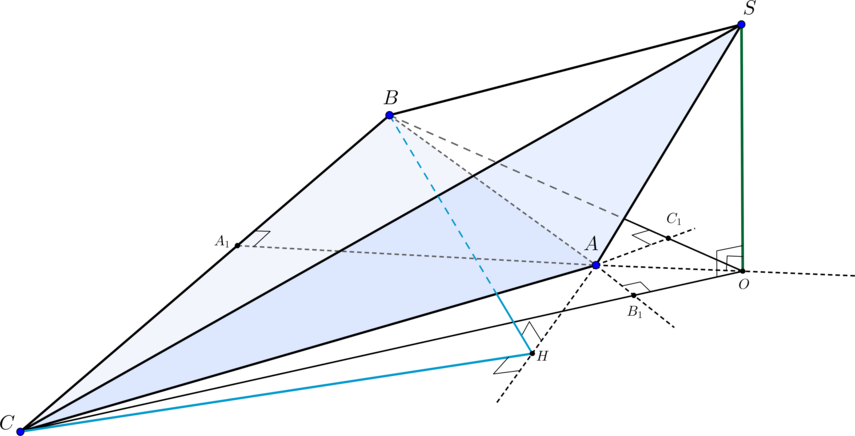
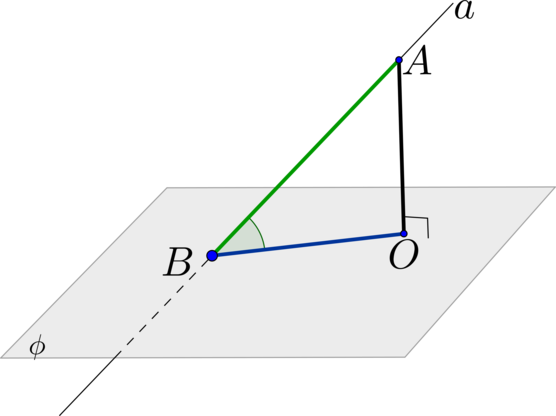
\(\blacktriangleright\) Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость (т.е. это острый или прямой угол).
\(\blacktriangleright\) Чтобы найти угол между прямой \(a\) и плоскостью \(\phi\) (\(a\cap\phi=B\)), нужно:
Шаг 1: из какой-то точки \(A\in a\) провести перпендикуляр \(AO\) на плоскость \(\phi\) (\(O\) – основание перпендикуляра);
Шаг 2: тогда \(BO\) – проекция наклонной \(AB\) на плоскость \(\phi\);
Шаг 3: тогда угол между прямой \(a\) и плоскостью \(\phi\) равен \(\angle
ABO\).
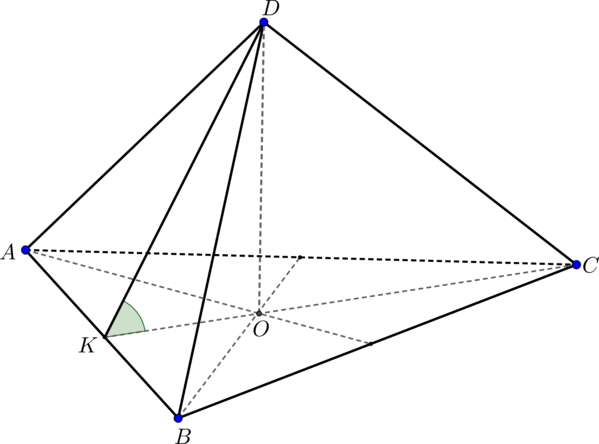
\(\blacktriangleright\) Двугранный угол – угол, образованный двумя полуплоскостями и прямой \(a\), которая является их общей границей.
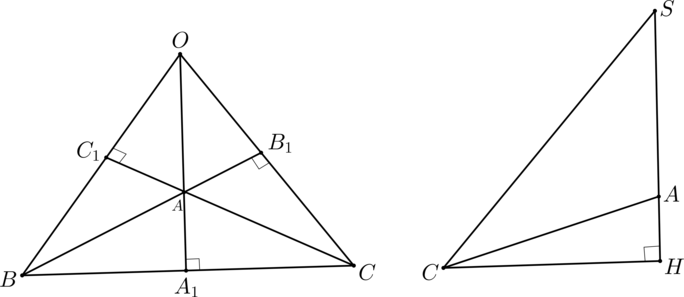
\(\blacktriangleright\) Чтобы найти угол между плоскостями \(\xi\) и \(\pi\), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями \(\xi\) и \(\pi\):
Шаг 1: пусть \(\xi\cap\pi=a\) (линия пересечения плоскостей). В плоскости \(\xi\) отметим произвольную точку \(F\) и проведем \(FA\perp
a\);
Шаг 2: проведем \(FG\perp \pi\);
Шаг 3: по ТТП (\(FG\) – перпендикуляр, \(FA\) –наклонная, \(AG\) – проекция) имеем: \(AG\perp a\);
Шаг 4: угол \(\angle FAG\) называется линейным углом двугранного угла, образованного плоскостями \(\xi\) и \(\pi\).
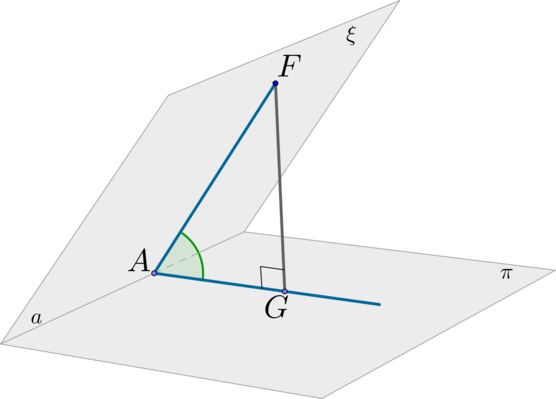
Заметим, что треугольник \(AG\) – прямоугольный.