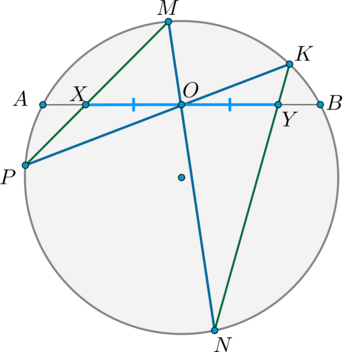
В окружность вписан четырехугольник \(MNKP\), причем площади треугольников \(MNP\) и \(MKP\) равны.
Докажите, что треугольник \(NOK\) – равнобедренный, где \(O\) – точка пересечения отрезков \(MK\) и \(NP\).
Т.к. \(S_{\triangle MNP}=S_{\triangle MKP}\) и эти треугольники имеют общее основание \(MP\), то \[\frac12\cdot MP\cdot NH_1=\frac12\cdot MP\cdot KH_2 \quad \Rightarrow \quad
NH_1=KH_2\]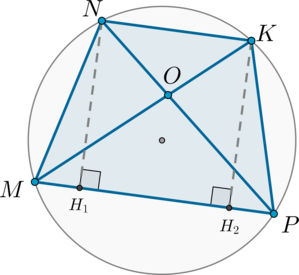
Таким образом, точки \(N\) и \(K\) находятся на одинаковом расстоянии от прямой \(MP\), следовательно, \(NK\parallel MP\). Таким образом, \(MNKP\) – трапеция, вписанная в окружность. Т.к. параллельные прямые отсекают от окружности равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{MN}=\buildrel\smile\over{KP}\). Т.к. равные дуги стягиваются равными хордами, то отрезки \(MN\) и \(KP\) равны. Следовательно, трапеция \(MNKP\) является равнобедренной.
В равнобедренной трапеции \(\triangle MOP\) и \(\triangle NOK\) являются равнобедренными, чтд.
Действительно, вписанные углы \(\angle NKM\) и \(\angle KNP\) равны, т.к. опираются на равные дуги, следовательно, \(\triangle NOK\) – равнобедренный.
Ответ:
Доказательство