Уровень составитель ЕГЭ. Тренировочный вариант №1

Билет со скидкой стоит \(12000 \cdot (1 - 0,06) = 11280\) рублей. Из группы в десять человек двое летели со скидкой, остальные восемь платили по \(12000\) рублей за билет. В сумме эти \(10\) пассажиров отдали \(12000 \cdot 8 + 11280 \cdot 2 = 118560\) рублей.

Ответ: 118560

По рисунку видно, что в первый раз за данный период Лера съела \(3\) конфеты через \(9\) дней после начала диеты.

Ответ: 9

Пусть \(\angle A = 60^{\circ}\). В ромбе все стороны равны, тогда треугольник \(ABD\) – равнобедренный, у которого один из углов равен \(60^{\circ}\), следовательно, треугольник \(ABD\) – равносторонний и \(BD = 10\).

Треугольник \(ABC\) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда \(AC > AB = BD\), значит, \(BD\) – меньшая из диагоналей.

Ответ: 10

Так как вероятности выбора любого числа из данного множества одинаковы, то искомая вероятность есть просто отношение количества чисел из данного множества, которые делятся на \(3\) или на \(4\), к количеству всевозможных чисел из данного множества.

Так как число от \(21\) до \(30\) не может одновременно делиться на \(3\) и на \(13\), то события \( \)“число делится на \(3\)”\(\ \)и\(\ \)“число делится на \(13\)”\( \) несовместны.

В данном множестве на \(3\) делятся: \(21\), \(24\), \(27\), \(30\), а на \(13\) делятся: \(26\). Всего в множестве натуральных чисел от \(21\) до \(30\) имеется \(10\) чисел, тогда вероятность того, что наугад взятое из них делится на \(3\) или на \(13\) равна \[\dfrac{5}{10} = 0,5.\]

Ответ: 0,5

Перепишем уравнение по убыванию степеней переменной:

\[-\dfrac1{\pi}x^3+\dfrac2{\pi}x^2+\pi x-2\pi=0.\]

По теореме Виета для уравнения третьей степени \(ax^3 + bx^2 + cx + d = 0\) сумма его корней (при учёте того, что все они различны) равна \(-\dfrac{b}{a}\), следовательно, сумма корней рассматриваемого уравнения равна \[-\dfrac{\frac{2}{\pi}}{-\frac{1}{\pi}} = 2.\]

Ответ: 2

В параллелограмме противоположные углы равны, а односторонние углы в сумме составляют \(180^{\circ}\).

Так как \(\sin{(\pi - \alpha)} = \sin{\alpha}\), то \(\sin{\angle A} + \sin{\angle B} + \sin{\angle C} + \sin{\angle D} = 4 \sin{\angle A}\), откуда находим \(\sin{\angle A} = 0,81\).

Площадь параллелограмма равна произведению двух его непараллельных сторон на синус угла между ними, тогда \[S_{ABCD} = 6\cdot 5\cdot 0,81 = 24,3.\]

Ответ: 24,3

Производная функции \(f(x)\) в точке \(x_0\) равна тангенсу угла наклона касательной к графику \(f(x)\) в точке \((x_0; f(x_0))\).

По рисунку видно, что касательная проходит через точки \((0,5; 1)\) и \((1,5; 1,5)\), тогда тангенс угла наклона касательной составляет \(0,5 : 1 = 0,5\), следовательно, \(f'(x_0) = 0,5\).

Ответ: 0,5

\(NM\) – средняя линия в треугольнике \(DBB_1\), тогда \(NM \parallel B_1D\) и \(\alpha\) равен углу между \(B_1D\) и плоскостью \((A_1B_1C_1D_1)\).

Так как \(DD_1\) – перпендикуляр к плоскости \(A_1B_1C_1D_1\), то \(B_1D_1\) проекция \(B_1D\) на плоскость \((A_1B_1C_1D_1)\) и угол между \(B_1D\) и плоскостью \((A_1B_1C_1D_1)\) есть угол между \(B_1D\) и \(B_1D_1\).

Пусть ребро куба \(x\), тогда по теореме Пифагора \[B_1D_1^2 = x^2 + x^2\qquad\Rightarrow\qquad B_1D_1 = x\sqrt{2},\] аналогично по теореме Пифагора \[B_1D = x\sqrt{3}.\] В треугольнике \(B_1D_1D\) тангенс угла между \(B_1D\) и \(B_1D_1\) равен \(\dfrac{DD_1}{B_1D_1} = \dfrac{1}{\sqrt{2}}\), откуда \(\mathrm{tg}^2\, \alpha = \dfrac{1}{2}\).

Ответ: 0,5

По определению логарифма \(\log_{17}289\) – это степень, в которую надо возвести 17, чтобы получить 289. Таким образом, \(\log_{17}289 = 2\). Аналогично можно сделать вывод, что \[\log_{500}\dfrac{1}{500} = -1.\] Итого: \((\log_{17}289) \cdot \left(\log_{500}\dfrac{1}{500}\right) = -2\).

Ответ: -2

Обозначим начальные параметры с индексом \(0\). При увеличении объема не менее чем в \(5\) раз имеем: \[\nu R T \geqslant 5pV_0 = 5\nu R T_0,\] откуда \(T \geqslant 5T_0\), то есть чтобы чтобы при неизменном давлении газа его объем вырос не менее чем в \(5\) раз надо увеличить его температуру минимум в \(5\) раз.

Ответ: 5

Пусть \(v\, км/ч\) – скорость лодки по пути от А до В, тогда

\(\dfrac{90}{v}\, ч\) – время, затраченное лодкой на путь из А в В,

\(\dfrac{45}{v + 5}\, ч\) – время, затраченное лодкой на первую половину пути из В в А,

\(\dfrac{45}{v - 2,5}\) – время, затраченное лодкой на вторую половину пути из В в А.

Так как в итоге лодка проплыла из В в А за такое же время, как и из А в В, то: \[\dfrac{90}{v} = \dfrac{45}{v + 5} + \dfrac{45}{v - 2,5},\] откуда \(v = 10\, км/ч\).

Ответ: 10

1) \(y' = e^{-x + \sqrt{2}} - (x + 1)\cdot e^{-x + \sqrt{2}} = -x\cdot e^{-x + \sqrt{2}}\).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[-x\cdot e^{-x + \sqrt{2}} = 0\qquad\Leftrightarrow\qquad x = 0\] (так как \(e^{t} > 0\) при любом \(t\)). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Эскиз графика \(y\):



Таким образом, \(x = 0\) – точка локального максимума функции \(y\).

Ответ: 0

а) ОДЗ: \(x\) – произвольное.
По формуле синуса двойного угла: \[2\sin x\cdot\cos x - 2\sqrt{3}\cos^2x-4\sin x + 4\sqrt{3}\cos x = 0.\] Сгруппируем первое и третье слагаемые, а также второе и четвертое:

\[\begin{aligned} 2\sin x(\cos x - 2) - 2\sqrt{3}\cos x(\cos x - 2) = 0\qquad\Leftrightarrow\qquad (\cos x - 2)(\sin x - \sqrt{3}\cos x) = 0. \end{aligned}\]

Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл: \[\cos x = 2\qquad \text{или}\qquad \sin x - \sqrt{3}\cos x = 0.\] Так как \(-1 \leqslant\cos x\leqslant 1\), то \(\cos x = 2\) не подходит.
\[\sin x - \sqrt{3}\cos x = 0.\] Так как те \(x\), при которых \(\cos x = 0\) не могут быть решениями, то на \(\cos x\) можно разделить: \[\mathrm{tg}\, x = \sqrt{3}.\]

Решения уравнения \(\mathrm{tg}\, x = a\) имеют вид \(x = \mathrm{arctg}\, a + \pi k\), где \(k\in\mathbb{Z}\), следовательно,   решения уравнения \(\mathrm{tg}\, x = \sqrt{3}\) имеют вид \(x = \dfrac{\pi}{3} + \pi k, k\in\mathbb{Z}\).

б) \[\pi \leqslant \dfrac{\pi}{3} + \pi k \leqslant \dfrac{5\pi}{2}\qquad\Leftrightarrow\qquad \dfrac{2}{3} \leqslant k \leqslant \dfrac{13}{6},\] но \(k\in\mathbb{Z}\), тогда подходят \(x\) при \(k = 1\) и \(k = 2\): \(x = \dfrac{4\pi}{3}\) и \(x = \dfrac{7\pi}{3}\).

Ответ:

а) \(\dfrac{\pi}{3} + \pi k, k\in\mathbb{Z}\).

б) \(\dfrac{4\pi}{3}\), \(\dfrac{7\pi}{3}\).

1) Пусть\(K\) – середина \(AC\), \(SX, AL\) – медианы грани \(ASB\), \(CL, SY\) – медианы грани \(CSB\), \(AL\cap SX=M, CL\cap SY=N\). \(SO\) – высота пирамиды.

Найдем сечение пирамиды плоскостью \(MNK\).
Т.к. пирамида правильная, то \(\triangle SXY\) – равнобедренный, \(SM=SN=\dfrac{2}{3}SX \Rightarrow MN\parallel XY \Rightarrow MN\parallel (ABC)\). Таким образом, плоскость \(MNK\) содержит прямую \(MN\), параллельную \(ABC\), следовательно, плоскость \(MNK\) пересечет плоскость \(ABC\) по прямой, параллельной \(MN\) (если это не так, то линия пересечения этих плоскостей \(l\cap MN=E \Rightarrow E\in (ABC)\) и \(E\in MN \Rightarrow MN\) не может быть параллельна \((ABC)\)).

Прямая, проходящая через точку \(K\) и параллельная \(MN\) (или \(XY\)) – это \(AC\). Следовательно, сечением является равнобедренный треугольник \(ALC\).

2) Пусть \(LK\cap SO=H\). Тогда по теореме о трех перпендикулярах \(HK\perp AC\) как наклонная (\(HO\perp (ABC), OK\perp AC\) как проекция). Следовательно, и \(LK\perp AC\).

Тогда \(S_{ALC}=\dfrac{1}{2}AC\cdot LK\).

Рассмотрим \(\triangle SKB: \ BK=AB\cdot \dfrac{\sqrt3}{2}=\dfrac{21\sqrt3}{2} \Rightarrow \cos B=\dfrac{7\sqrt3}{12\sqrt2}\).

Тогда по теореме косинусов для \(\triangle KLB\):

\(KL^2=\dfrac{729}{4} \Rightarrow KL=\dfrac{27}{2}\)

Значит, \(S_{ALC}=\dfrac{567}{4}\).

Ответ:

\(\dfrac{567}{4}\).

ОДЗ: \(x\) – произвольный.

Так как \(\log_5 15625 = \log_5 5^6 = 6\), то исходное неравенство равносильно неравенству

\[\begin{aligned} 125^x + 6\cdot 25^x + 11\cdot 5^x + 6\leqslant 0 \end{aligned}\]

Сделаем замену \(5^x = t > 0\):

\[\begin{aligned} t^3 + 6t^2 + 11t + 6\leqslant 0 \end{aligned}\]

Можно угадать корень левой части последнего неравенства: \(t = -1\). Знание корня многочлена позволяет поделить его столбиком на \(t - t_0\), где \(t_0\) – его корень, тогда \[\begin{array}{rr|l} t^3+6t^2+11t+6&&\negthickspace\underline{\qquad t+1 \qquad}\\ \underline{t^3+\ t^2} \phantom{000000000}&&\negthickspace \ t^2 + 5t + 6\\[-3pt] 5t^2 + 11t\,\phantom{000}&&\\ \underline{5t^2 + 5t\,}\phantom{000}&&\\[-3pt] 6t + 6 &&\\ \underline{6t + 6}&&\\[-3pt] 0&&\\ \end{array}\]

Таким образом, последнее неравенство равносильно

\[\begin{aligned} (t + 1)(t^2 + 5t + 6)\leqslant 0\qquad\Leftrightarrow\qquad (t + 1)(t + 2)(t + 3)\leqslant 0, \end{aligned}\]

то есть оно не выполняется при \(t > 0\), следовательно, ответ: \[x\in\varnothing\,.\]

Ответ:

\(\varnothing\)

а) Если около четырёхугольника \(ABCD\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).

Если около четырёхугольника \(ACDE\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).

Если около четырёхугольника \(ACDF\) можно описать окружность, то она будет описанной и для треугольника \(ACD\).

Так как около треугольника можно описать ровно одну окружность, то описанные около четырёхугольников \(ABCD\), \(ACDE\) и \(ACDF\) окружности должны совпасть, следовательно, тогда шестиугольник \(ABCDEF\) также будет вписанным.

Таким образом, достаточно показать, что около \(ABCDEF\) нельзя описать окружность.

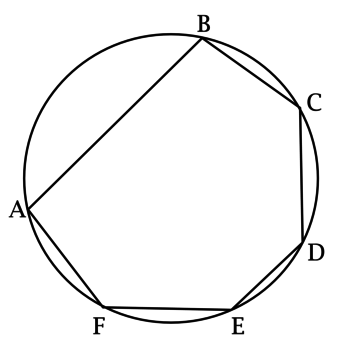
Пусть шестиугольник \(ABCDEF\) – вписанный, тогда

\[\begin{aligned} &\angle A + \angle C + \angle E = 0,5\cdot\smile BCDEF + 0,5\cdot\smile BAFED + 0,5\cdot\smile FABCD =\\ &= 0,5(360^\circ - \smile BAF) + 0,5(360^\circ - \smile BCD) + 0,5(360^\circ - \smile FED) =\\ &= 540^\circ - 0,5(\smile BAF + \smile BCD + \smile FED) = 360^\circ, \end{aligned}\]

но \(\angle A + \angle C + \angle E > 360^\circ\), следовательно, около \(ABCDEF\) нельзя описать окружность, откуда следует, что около хотя бы одного из четырёхугольников \(ABCD\), \(ACDE\) и \(ACDF\) нельзя описать окружность.

б)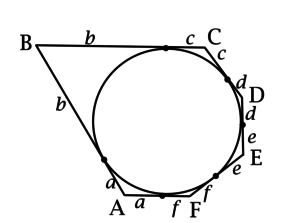

Пользуясь тем, что отрезки касательных к окружности, проведённых из одной точки, равны, обозначим длины отрезков касательных, проведённых из точки \(A\), через \(a\), длины отрезков касательных, проведённых из точки \(B\), через \(b\) и т.д.

\[11 = AB + CD + EF = a + b + c + d + e + f = 0,5\cdot P_{ABCDEF},\] откуда \(P_{ABCDEF} = 22\).

Ответ:

б) \(22\).

Составим таблицу, обозначив за \(t=\dfrac{100+y}{100}, \ A=351\,000\): \[\begin{array}{|l|c|c|c|} \hline \text{Год} & \text{Сумма на счете} & \text{Сумма на счете} & \text{Сумма на счете}\\ & \text{до начисления }\% & \text{после начисления }\% & \text{после дополнительного взноса} \\ \hline &&&\\ 1 & A & t A & t A+\dfrac{1}{3}A\\ &&&\\ \hline &&&\\ 2 & tA+\dfrac{1}{3}A & t\left(tA+\dfrac{1}{3}A\right) & t\left(tA+\dfrac{1}{3}A\right)+\dfrac{1}{3}\left(tA+\dfrac{1}{3}A\right) \\ &&&\\ \hline \end{array}\]

Таким образом, на начало третьего года на счете у Елены будет та же сумма, которая была на счете на конец второго года после начисления процентов и после внесения второго дополнительного взноса, т.е.

\(t\left(tA+\dfrac{1}{3}A\right)+\dfrac{1}{3}\left(tA+\dfrac{1}{3}A\right)\).

Необходимо, чтобы \(t(tA+\dfrac{1}{3}A)+\dfrac{1}{3}(tA+\dfrac{1}{3}A) \leqslant 1\,092\,000\)

Заметим, что \(1\,092\,000=\dfrac{28\cdot 351\,000}{9}=\dfrac{28}{9}A \Rightarrow\) неравенство примет вид:

\(3t^2+2t-9 \leqslant 0 \Rightarrow t \leqslant \dfrac{2\sqrt7-1}{3}\), т.к. \(t>0\).

Значит, \( y \leqslant \dfrac{200}{3}(\sqrt7-2)\)

Оценим \(\dfrac{200}{3}(\sqrt7-2)\):

\(2645<\sqrt{7000000}<2646 \Rightarrow\\ 2645<1000\sqrt7<2646 \Rightarrow\\ 0,645<\sqrt7-2<0,646 \Rightarrow\\ \\ 43<\dfrac{200}{3}(\sqrt7-2)<\dfrac{129,2}{3}\)

Таким образом, т.к. \(\dfrac{129,2}{3}=43\dfrac{1}{15}\), наибольшее целое \(y=43 \%\).

Ответ:

\(43\%\).

Рассмотрим два случая:

1) \(a=0\). Тогда уравнение становится линейным и \(x=-\dfrac{1}{4}\). Это значения параметра нам не подходит.

2) \(a\ne 0\). Тогда уравнение является квадратным.Его дискриминант \(D=4(4-a^2-a)\).

а) Если \(D=0 \Rightarrow a=\dfrac{-1\pm \sqrt{17}}{2} \Rightarrow\) уравнение \(ax^2+4x+a+1=0\) имеет один корень \(x=-\dfrac{2}{a}\).

При \(a=\dfrac{-1+ \sqrt{17}}{2}\) это корень \(x=-\dfrac{4}{\sqrt{17}-1}<0<1\), следовательно, это значение параметра не подходит.

При \(a=\dfrac{-1- \sqrt{17}}{2}\) это корень \(x=\dfrac{4}{\sqrt{17}+1}=\dfrac{4(\sqrt{17}-1)}{\sqrt{17}^2-1^2}=\dfrac{\sqrt{17}-1}{4}<1\),

следовательно, это значение параметра также не подходит.

б) Если \(D>0 \Rightarrow a\in \left(\dfrac{-1- \sqrt{17}}{2} ;\dfrac{-1+ \sqrt{17}}{2} \right) \Rightarrow\) уравнение \(ax^2+4x+a+1=0\) имеет два корня.

Графиком функции \(f(x)=ax^2+4x+a+1\) при каждом фиксированном \(a\) является парабола,

причем при \(a\in \left(0;\dfrac{-1+ \sqrt{17}}{2}\right)\) ветви направлены вверх, при \(a\in \left(\dfrac{-1- \sqrt{17}}{2};0\right)\) ветви направлены вниз:

Для того, чтобы уравнение имело ровно один корень больше \(1\), нужно:

\[\left[ \begin{gathered} \begin{aligned} &\begin{cases} 0<a<\dfrac{-1+ \sqrt{17}}{2}\\ f(1)<0 \end{cases}\\[5pt] &\begin{cases} \dfrac{-1- \sqrt{17}}{2}<a<0\\ f(1)>0 \end{cases} \end{aligned} \end{gathered} \right. \quad \Longrightarrow \quad -\dfrac{5}{2}<a<0\]

Ответ:

\(a\in \left(-\dfrac{5}{2};0\right)\).

Всего при делении на \(n\) существует \(n\) различных остатков, а так как чисел \(n+1\), то по принципу Дирихле найдутся \(2\) числа с одинаковыми остатками, следовательно, их разность будет делиться на \(n\).

Ответ:

Доказательство