Задачи по планиметрии

\(\triangle ABC\) и \(\triangle MBN\) имеют общий угол \(B\), при этом \(BM=\frac23BA\), \(BN=\frac13BC\).

Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то

\[\dfrac{S_{MBN}}{S_{ABC}}=\dfrac{\frac23BA\cdot \frac13BC}{BA\cdot BC}= \dfrac29 \quad \Rightarrow \quad S_{MBN}=\dfrac29S_{ABC}\]

Аналогично рассуждая, получаем, что

\[S_{MAP}=S_{PCN}=\dfrac29S_{ABC}\]

Следовательно, \[15+3\cdot \dfrac29S_{ABC}=S_{ABC} \quad \Rightarrow \quad S_{ABC}=3\cdot 15=45.\]

Ответ: 45

Соединим точки \(A\) и \(C_1\), \(B\) и \(A_1\), \(C\) и \(B_1\).

Т.к. медиана делит треугольник на два равновеликих треугольника, то

\[S_{\triangle AB_1C}=S_{\triangle A_1B_1C}=S_{\triangle A_1B_1C_1}.\]

Аналогично,

\[S_{\triangle CA_1B}=S_{\triangle C_1A_1B}=S_{\triangle AC_1B}=S_{\triangle AC_1B_1}.\]

Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,

\[S_{\triangle A_1B_1C_1}:S_{\triangle ABC}=1:7.\]

Ответ:

\(1:7\)

Пусть \(S_{\bigtriangleup BOC}=x\). Заметим, что \(\bigtriangleup BCO \sim \bigtriangleup AOD\) по двум углам, так как \(BC\parallel AD\), \(\angle BCA = \angle CAD\) как накрест лежащие и \(\angle BOC = \angle AOD\) как вертикальные.

Следовательно, \[\dfrac{BC}{AD} =\dfrac{BO}{OD} =\dfrac{CO}{OA} =\dfrac{2}{6} =\dfrac{1}{3}.\]

\(\dfrac{S_{\bigtriangleup ABO}}{S_{\bigtriangleup BCO}} =\dfrac{AO}{OC} =\dfrac{3}{1} \Rightarrow \ S_{\bigtriangleup ABO}=3x\), аналогично, \(S_{\bigtriangleup CDO}=3x\).  

\(\dfrac{S_{\bigtriangleup COP}}{S_{\bigtriangleup CPD}} =\dfrac{OP}{PD} =\dfrac{1}{1} \Rightarrow \ S_{\bigtriangleup COP}=S_{\bigtriangleup CPD}=1,5x\).  

Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, \[\dfrac{S_{\bigtriangleup BOC}}{S_{\bigtriangleup AOD}} =\left( \dfrac{1}{3} \right)^2 =\dfrac{1}{9} \ \Rightarrow\ S_{\bigtriangleup ADO}=9x \ \Rightarrow\ S_{\bigtriangleup APO}=4,5x \ \Rightarrow\qquad S_{ABCP}=10x.\] Так как \(3x=9\), то \(x=3\) и, следовательно, \(S_{ABCP}=30\).

Ответ: 30

Рассмотрим равносторонний \(\triangle ABC\), \(AB=m\), \(O\) – точка внутри треугольника, \(OA_1, OB_1, OC_1\) — перпендикуляры на стороны \(BC, AC, AB\) соответственно.

Рассмотрим \(\triangle AOB, \ \triangle BOC, \ \triangle COA\). Их площади равны \(0,5m\cdot OC_1; \ 0,5m\cdot OA_1; \ 0,5m\cdot OB_1\) соответственно. Тогда сумма их площадей равна площади всего \(\triangle ABC\), следовательно:

\[0,5m\cdot (OC_1+OA_1+OB_1)=S_{\triangle ABC}=\dfrac{\sqrt3}4m^2 \quad \Leftrightarrow \quad OC_1+OA_1+OB_1=\dfrac{\sqrt3}2m.\]

Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.

Ответ:

\(\dfrac{\sqrt3}2m\)

а) \(S_{ABC} = p\cdot r\), где \(p\) – полупериметр, а \(r\) – радиус вписанной в \(ABC\) окружности.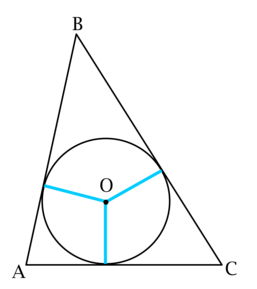

Пусть \(h\) – длина той высоты, которая равна \(3r\), \(a\) – длина стороны, высота к которой имеет длину \(h\), \(P\) – периметр треугольника \(ABC\).

В итоге имеем: \[\dfrac{1}{2}h\cdot a = S_{ABC} = p\cdot r = p\cdot\dfrac{h}{3},\] откуда \(a = \dfrac{P}{3}\), тогда \(b + c = \dfrac{2P}{3} = 2a\), где \(b\) и \(c\) длины других сторон треугольника.

б) Длины сторон треугольника \(ABC\) образуют арифметическую прогрессию: если обозначить \(a - c = d\), то \(a = c + d\), \(b = c + 2d\).

Пусть \(d > 0\). Тогда \(b\) наибольшая сторона треугольника \(ABC\) и существование треугольника \(ABC\) с длинами сторон \(a\), \(b\) и \(c\) равносильно выполнению неравенства \[b < a + c\qquad\Leftrightarrow\qquad c + 2d < 2c + d\qquad\Leftrightarrow\qquad d < c.\] Так как длины всех сторон треугольника \(ABC\) – целые числа, то \(d\) – целое, следовательно, \(d\leq c - 1\).

Так как \(c\) – меньшая из сторон, то \(c\leq 4\), тогда \(d\leq 3\), откуда \(a\leq 7\), \(b\leq 10\), тогда \[P_{\triangle ABC}\leq 4 + 7 + 10 = 21.\] При этом случай \(c = 4\), \(a = 7\), \(b = 10\) подходит, следовательно, при \(d > 0\) максимально возможный периметр равен 21.

При \(d = 0\) треугольник \(ABC\) равносторонний и \(P_{\triangle ABC} = 12 < 21\).

Случай \(d < 0\) рассматривается аналогично (меняется только то, что \(c > a > b\), следовательно, достаточно в рассуждении из случая \(d > 0\) всюду поменять местами \(b\) и \(c\)).

Таким образом, наибольший возможный периметр треугольника \(ABC\) равен 21.

Ответ:

б) \(21\).

а) Так как \(\dfrac{MN}{PQ} = \dfrac{QM}{PN}\), то \(MN\cdot PN = QM\cdot PQ\).

Так как \(MNPQ\) вписанный, то \(\angle MNP = 180^\circ - \angle MQP\), следовательно, \(\sin\angle MNP = \sin\angle MQP\).

В итоге \[S_{\triangle MNP} = 0,5\cdot MN\cdot PN\cdot\sin\angle MNP = 0,5\cdot QM\cdot PQ\cdot\sin\angle MQP = S_{\triangle MQP}.\]

С другой стороны, у треугольников \(MNP\) и \(MQP\) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки \(N\) и \(Q\) равноудалены от прямой, содержащей \(MP\).

б) В данном случае \(S_{\triangle MNP} = 0,5\cdot 4\cdot 1,5 = 3\), но \(S_{\triangle MNP} = S_{\triangle MQP}\). Обозначим расстояние от точки \(P\) до прямой, содержащей \(MQ\) через \(h\), тогда \[S_{\triangle MQP} = 3 = 0,5\cdot 3\cdot h,\] следовательно, \(h = 2\).

Ответ:

б) \(2\).

а) Проведём диагонали \(AC\) и \(BD\).

Рассмотрим треугольники \(APS\) и \(ABD\): \(PS\) – средняя линия в треугольнике \(ABD\), тогда треугольники \(APS\) и \(ABD\) подобны, причём \(\dfrac{PS}{BD} = \dfrac{1}{2}\).

Аналогично \(\dfrac{QR}{BD} = \dfrac{1}{2}\), следовательно, \(PS = QR\).

Аналогично доказывается равенство \(PQ = RS\). В итоге в выпуклом четырёхугольнике \(PQRS\) противоположные стороны равны, тогда \(PQRS\) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.

б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.

Из подобия \(APS\) и \(ABD\) получаем: \[\dfrac{S_{APS}}{S_{ABD}} = \left(\dfrac{1}{2}\right)^2 = \dfrac{1}{4}.\]

Аналогично \(4S_{QCR} = S_{CBD}\), \(4S_{PBQ} = S_{ABC}\), \(4S_{SDR} = S_{ACD}\). Тогда \[S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.\] С другой стороны, \[S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},\] тогда \[S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} \qquad\Leftrightarrow\] \[S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = \dfrac{1}{2}S_{ABCD}.\] Но \(S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}\), откуда окончательно \[S_{PQRS} = \dfrac{1}{2}S_{ABCD}.\]

Таким образом, по взаимному расположению точек \(P\), \(Q\), \(R\), \(S\) однозначно восстанавливается площадь параллелограмма \(PQRS\), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках \(P\), \(Q\), \(R\) и \(S\).

В итоге \[\dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.\]

Ответ:

б) \(1\).