1 способ.
1) Рассмотрим случай, когда \(a>0\). В этом случае систему можно переписать в виде: \[\begin{cases} x\geqslant \dfrac2a\\[2ex]
x\leqslant \dfrac{2a+11}3\\[2ex]
x>a^2+1 \end{cases} \qquad (*)\]
Для того, чтобы система имела решения, нужно, чтобы \[\begin{cases}
\dfrac2a\leqslant \dfrac{2a+11}3\\[3ex]
a^2+1<\dfrac{2a+11}3\end{cases}\]
Решением неравенства \(\dfrac2a\leqslant \dfrac{2a+11}3\) будут \(a\in
(-\infty;-6]\cup\left[\frac12;+\infty\right)\). Так как \(a>0\), то подходит только \(a\geqslant \dfrac12\).
Решением неравенства \(a^2+1<\dfrac{2a+11}3\) будут \(a\in (0;2)\). Следовательно, пересекая полученные решения, имеем: \(a\in
\left[\frac12;2\right)\). Таким образом, при этих \(a\) система \((*)\) будет иметь решения.
Теперь посмотрим, когда хотя бы одно из этих решений будет лежать в отрезке \([3;4]\).
Заметим, что при полученных \(a\) числа \(\dfrac2a; \ a^2+1; \
\dfrac{2a+11}3\) могут располагаться в следующем порядке: \[\begin{aligned}
& I. \quad \dfrac2a; \ a^2+1; \ \dfrac{2a+11}3 \quad
\Rightarrow\quad {\small{\text{тогда решением системы (*) будут }}}
x\in \left(a^2+1;\dfrac{2a+11}3\right]\\[4ex]
& II. \quad \dfrac2a=a^2+1; \ \dfrac{2a+11}3 \quad \Rightarrow\quad
{\small{\text{тогда решением системы (*) будут }}} x\in
\left(a^2+1;\dfrac{2a+11}3\right]\\[4ex]
& III. \quad a^2+1; \ \dfrac2a; \ \dfrac{2a+11}3 \quad
\Rightarrow\quad {\small{\text{тогда решением системы (*) будут }}}
x\in \left[\dfrac2a;\dfrac{2a+11}3\right] \end{aligned}\]
\(I\) и \(II\) случаи задаются условием \(\dfrac2a\leqslant a^2+1\).
В этих случаях для того, чтобы хотя бы одно решение попало в отрезок \([3;4]\), нужно, чтобы \(a^2+1<4\).
Следовательно, решим систему: \[\begin{cases}
\dfrac2a\leqslant a^2+1\\[2ex]
a^2+1<4 \end{cases} \quad\Rightarrow\quad \begin{cases}
a^3+a-2\geqslant 0\\
a^2<3 \end{cases}\quad\Rightarrow\quad \begin{cases}
(a-1)(a^2+a+2)\geqslant 0\\
a^2<3 \end{cases}\] Следовательно, учитывая, что \(a\in
\left[\frac12;2\right)\), решением системы будут: \(a\in
[1;\sqrt3)\).
Случай \(III\) задается условием \(a^2+1<\dfrac2a\).
В этом случае для того, чтобы хотя бы одно решение попало в отрезок \([3;4]\), нужно, чтобы \(\dfrac2a\leqslant 4\).
Следовательно, решим систему: \[\begin{cases}
a^2+1<\dfrac2a\\[2ex]
\dfrac2a\leqslant 4 \end{cases} \quad\Rightarrow\quad \begin{cases}
a^3+a-2<0\\
a\geqslant \dfrac12 \end{cases}\] Следовательно, учитывая, что \(a\in
\left[\frac12;2\right)\), решением системы будут: \(a\in
\left[\frac12;1\right)\).
Так как нам подходит или случай \(I\), или \(II\), или \(III\), то значения \(a\), полученные в этих случаях, нужно объединить. Объединяя \(\left[\frac12;1\right)\) и \([1;\sqrt3)\), получим \[a\in \left[\dfrac12;\sqrt3\right).\]
2 способ.
Так как нужно, чтобы система имела хотя бы одно решение из отрезка \([3;4]\), то как минимум \(x>0\). Следовательно, решим систему только для \(x>0\). В таком случае можно разделить первое неравенство на \(x\) и получим следующую систему: \[\begin{cases}
a\geqslant \dfrac2x\\[3ex]
a\geqslant \dfrac32x-\dfrac{11}2\\[3ex]
a<\sqrt{x-1} \end{cases}\]
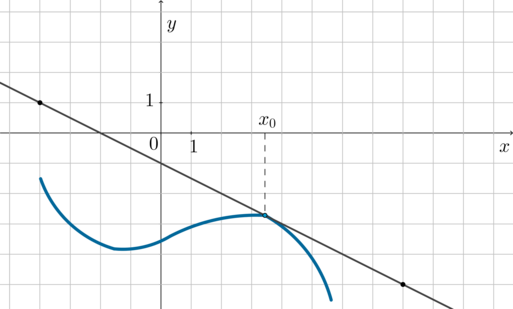
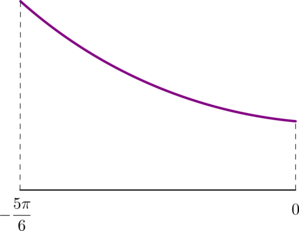
Рассмотрим систему координат \(xOa\) (то есть привычная нам ось \(Oy\) будет называться \(Oa\)). Тогда каждое неравенство при \(x>0\) задает некоторую область, а решением системы является область, равная пересечению всех трех областей, как показано на рисунке (белая область и есть решение системы):
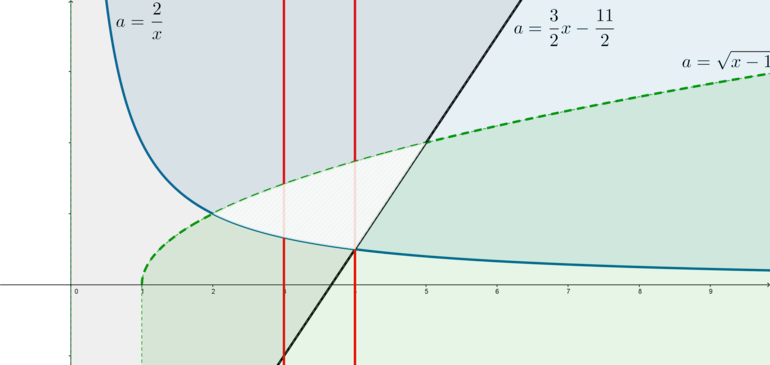
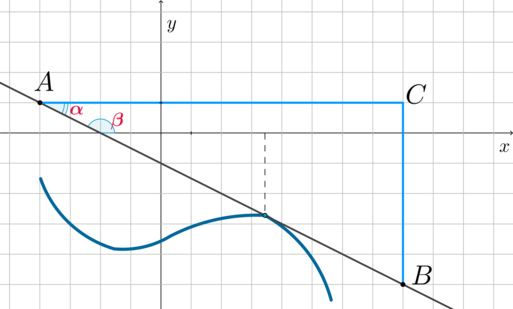
Тогда условие “система имеет хотя бы одно решение из отрезка \([3;4]\)” задает область:
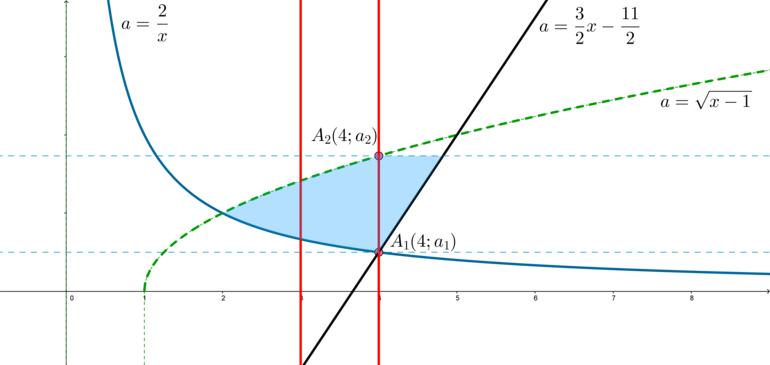
Следовательно, \(a\in \left[a_1;a_2\right)\), где \(a_1, a_2\) – ординаты точек пересечения прямой \(x=4\) с \(a=\dfrac2x\) и \(x=4\) с \(a=\sqrt{x-1}\).
(Заметим, что значение \(a_1\) включается, так как неравенство \(a\geqslant \dfrac2x\) не строгое, а \(a_2\) не включается, так как неравенство \(a<\sqrt{x-1}\) строгое.)
Таким образом, \(a_1=\dfrac24=\dfrac12\), а \(a_2=\sqrt{4-1}=\sqrt3\). Следовательно, ответ \(a\in \left[\dfrac12;\sqrt3\right).\)
Ответ:
\(\left[\dfrac12;\sqrt3\right)\)