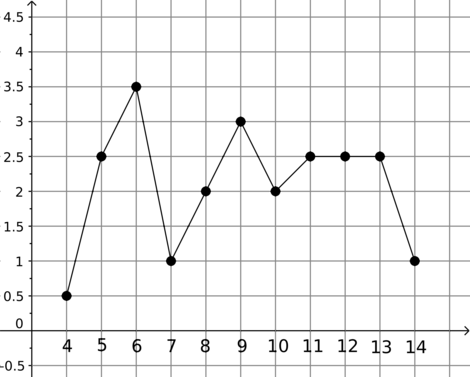
В понедельник Ивана повысили, вследствие чего его зарплата выросла на \(10\%\). Во вторник Ивана снова повысили, в следствие чего его зарплата снова выросла на \(10\%\). В среду Иван взял ипотеку, и теперь он должен каждый месяц отдавать \(20\%\) зарплаты банку. Иван не сказал жене ни о повышениях, ни об ипотеке. Раньше Иван всю зарплату отдавал жене, теперь он отдаёт жене всю зарплату, остающуюся после уплаты ипотеки. На сколько процентов, по мнению жены, упала зарплата Ивана?
Пусть изначальная зарплата Ивана составляла \(S\), тогда в понедельник его зарплата составила \(S\cdot (1 + 0,1) = 1,1\cdot S\). Во вторник зарплата Ивана составила \(1,1\cdot S\cdot (1 + 0,1) = 1,21\cdot S\). После уплаты ипотеки Иван относит жене \(1,21\cdot S\cdot (1 - 0,2) = 0,968\cdot S\). Таким образом, по мнению жены, новая зарплата Ивана составляет от старой \[\dfrac{0,968\cdot S}{S}\cdot 100\% = 96,8\%\,,\] следовательно, по мнению жены, зарплата Ивана упала на \(100\% - 96,8\% = 3,2\%\).
Ответ: 3,2