1 способ. Графический.
Заметим, что графиком первого уравнения является окружность при всех \(a\ne 0\).
Графиком второго уравнения при всех \(a^2-3a\ne 0\) является гипербола. Поэтому рассмотрим вырожденные случаи отдельно:
1) \(a=0\). Тогда решением первого уравнения будет единственная пара \(x=0, y=0\). Следовательно, уже система не будет иметь 2 решения. Значит, это значение \(a\) нам не подходит.
2) \(a=3\). Тогда графиком первого уравнения будет окружность с центром в \((0;0)\) и радиусом \(3\).
Второе уравнение примет вид \(xy=0\) и его графиком будут две прямые: \(x=0\) и \(y=0\).
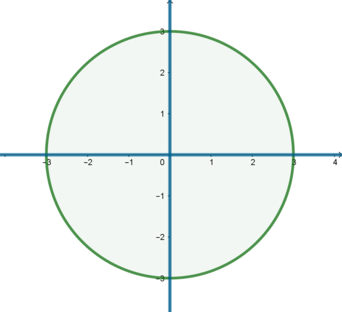
Видим, что графики уравнений имеют 4 точки пересечения, следовательно, исходная система при \(a=3\) имеет 4 различных решения. Значит, это значение \(a\) нам также не подходит.
3) \(a\ne 0;3\). Тогда график первого уравнения – окружность с центром в \((0;0)\) и радиусом \(R=\sqrt{a^2}=|a|\).
График второго уравнения – гипербола \(y=\frac{a^2-3a}x\) (можем делить на \(x\), так как если \(a^2-3a\ne 0\), то и \(xy\ne 0\), следовательно, и \(x\ne 0\)).
При \(a^2-3a>0\) ветви гиперболы будут находиться в \(I\) и \(III\) четвертях, при \(a^2-3a<0\) – во \(II\) и \(IV\) четвертях:
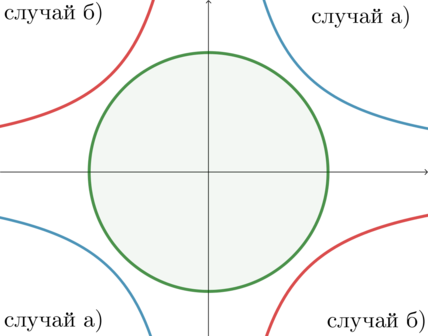
Случай а).
Чтобы исходная система имела 2 решения, нужно, чтобы гипербола касалась окружности (будут две точки касания). Заметим, что картинки в \(I\) и в \(III\) четвертях симметричны относительно начала координат. Следовательно, можно рассматривать только \(I\) четверть.
Заметим также, что окружность, как и гипербола, симметрична относительно прямой \(y=x\). Следовательно, если они и касаются, то точка касания \(K\) находится на прямой \(y=x\):
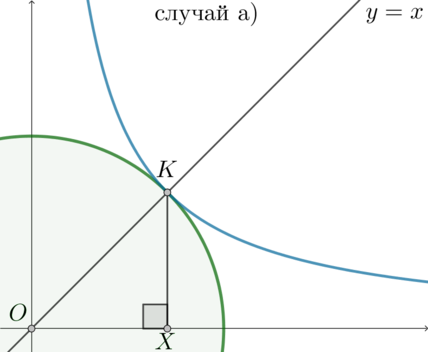
Пусть \(K=(x_0;x_0)\). Проведем \(KX\perp Ox\). Тогда \(OX=x_0\). Так как \(OK=|a|\), \(\triangle OKX\) прямоугольный и равнобедренный, то \(OX=|a|:\sqrt2\).
Так как \(K\) – точка касания, то \(K\) лежит на гиперболе. Следовательно, если подставить координаты точки \(K\) в уравнение гиперболы, получится верное равенство (из которого мы как раз и найдем \(a\)): \[\dfrac{|a|}{\sqrt2}=\dfrac{a^2-3a}{\frac{|a|}{\sqrt2}}\quad\Rightarrow\quad
\dfrac{a^2}2=a^2-3a\quad\Leftrightarrow\quad a=0; 6\] Так как в случае а) \(a^2-3a>0\), то подходит только \(a=6\).
Случай б).
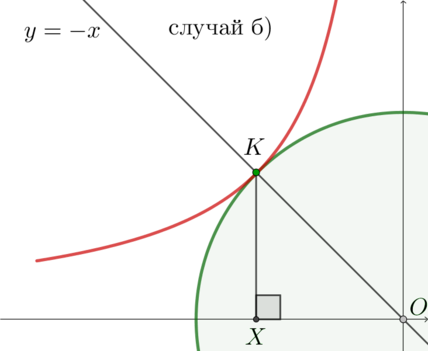
Он аналогичен случаю а) за исключением одного момента: у точки \(K\) координаты противоположны, то есть \((x_0;-x_0)\). Следовательно, когда мы будем поставлять их в уравнение гиперболы, получим: \[-\dfrac{|a|}{\sqrt2}=\dfrac{a^2-3a}{\frac{|a|}{\sqrt2}}
\quad\Rightarrow\quad a=0;2\] Так как в этом случае \(a^2-3a<0\), то подходит \(a=2\).
Ответ: \(a=2;6\).
2 способ. Алгебраический.
Перепишем систему в виде: \[\begin{cases}
x^2+y^2=a^2\\
2xy=2a^2-6a \end{cases} \quad\Leftrightarrow\quad
\begin{cases}
(x+y)^2=3a^2-6a\\
(x-y)^2=6a-a^2 \end{cases}\qquad(*)\] Таким образом, чтобы система имела решения, как минимум нужно, чтобы \[\begin{cases} 3a^2-6a\geqslant 0\\
6a-a^2\geqslant 0\end{cases} \quad\Leftrightarrow\quad a\in
\{0\}\cup[2;6]\]
1) Если \(a=0\), то получаем: \[\begin{cases} (x+y)^2=0\\(x-y)^2=0
\end{cases} \quad\Leftrightarrow\quad x=y=0\] Одно решение. Следовательно, \(a=0\) не подходит.
2) Пусть \(a\in [2;6]\).
Перепишем систему в виде (\(A^2=3a^2-6a\), \(B^2=6a-a^2\)): \[\begin{cases}
(x+y)^2=A^2\\
(x-y)^2=B^2 \end{cases}\] 2.1) Заметим, что если \(A\ne 0\), то первое уравнение имеет два различных решения \(x+y=A\) и \(x+y=-A\).
Аналогично со вторым уравнением и \(B\ne 0\).
Значит, если \(A\ne 0, B\ne 0\), то для чисел \((x+y; x-y)\) мы имеем четыре различные пары решений \((A;B)\), \((A;-B)\), \((-A;B)\), \((-A;-B)\). Но тогда мы будем иметь четыре различные пары решений для \((x;y)\).
2.2) Если одно из \(A, B\) равно нулю, а другое – нет, то мы будем иметь две различные пары решений для \((x+y; x-y)\): либо \((A;0)\) и \((-A;0)\), либо \((0;B)\) и \((0;-B)\).
2.3) \(A\) и \(B\) одновременно не могут быть равны нулю (тогда \(a=0\), а мы этот случай уже рассмотрели и отбросили).
Таким образом, единственный случай, который нам подходит – это случай 2.2): \[\begin{cases}
a\ne 0 \\ \left[\begin{gathered}\begin{aligned} &A=0 \\ &B=0
\end{aligned}\end{gathered}\right.\end{cases} \quad\Rightarrow\quad a=2;6\]
Ответ:
\(\{2;6\}\)