7. Взаимосвязь функции и ее производной
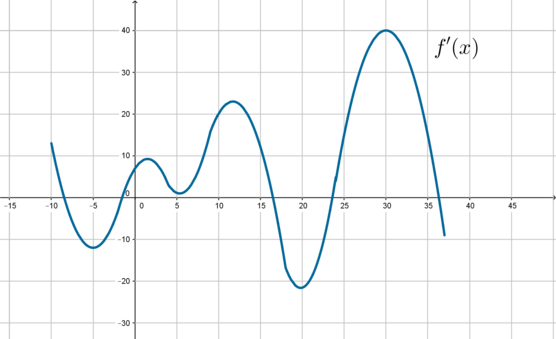
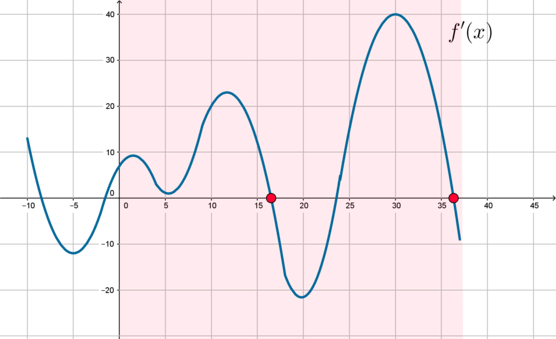
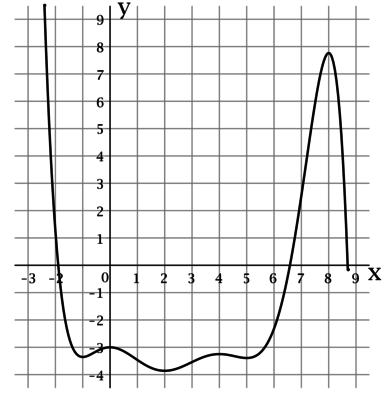
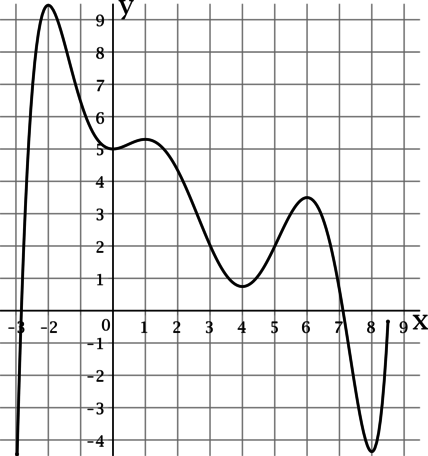
В данных задачах речь идет о непрерывных функциях (простым языком, функция будет непрерывна на интервале, если ее график можно нарисовать на этом интервале, не отрывая ручку от листа).
\(\blacktriangleright\) \(\color{royalblue}{\text{Точки}}\) (локального) \(\color{royalblue}{\text{экстремума}}\) функции – это точки (локального) максимума и минимума.
Окрестность – это интервал вокруг точки некоторого радиуса. Например, окрестностью точки \(x=0\) можно назвать интервал \((-1;1)\), или \((-0,1;0,1)\), или \((-0,0000001;0,0000001)\) и т.д.
\(\blacktriangleright\) \(\color{royalblue}{\text{Точка}}\) \(\color{royalblue}{\text{максимума}}\) \(x_{max}\) – такая внутренняя точка области определения функции, для которой выполнено: \(f(x)\leqslant f(x_{max})\) для любого \(x\) из некоторой окрестности точки \(x_{max}\).
То есть можно найти такую окрестность, что для любой точки из этой окрестности будет выполнено данное неравенство.
Заметим, что, например, если функция определена на отрезке \([0;2]\), то все точки интервала \((0;2)\) будут внутренними, а вот точки \(0\) и \(2\) – граничными (то есть не внутренними).
\(\blacktriangleright\) \(\color{royalblue}{\text{Точка}}\) \(\color{royalblue}{\text{минимума}}\) \(x_{min}\) – такая внутренняя точка области определения функции, для которой выполнено: \(f(x)\geqslant
f(x_{min})\) для любого \(x\) из некоторой окрестности точки \(x_{min}\).
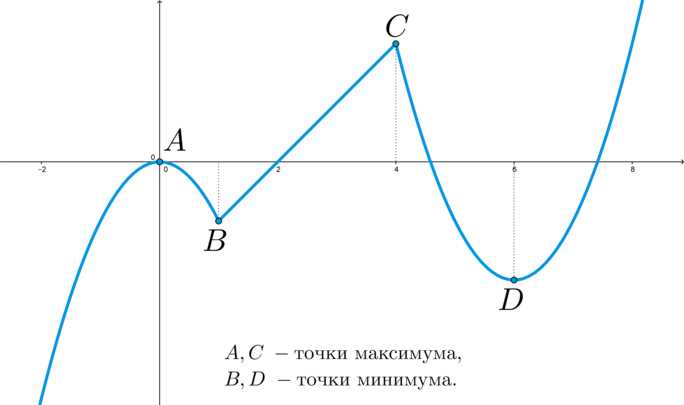
Например, для точки \(C\) за окрестность можно взять интервал \((3;5)\) или даже \((2;6)\), а можно совсем маленький — \((4-0,01;4+0,01)\).
Следующие факты помогают искать точки экстремума функции.
\(\blacktriangleright\) Если производная \(f'\) в точке \(x\) равна нулю и меняет свой знак слева направо с “\(+\)” на “\(-\)” , то эта точка является точкой максимума.
Заметим также, что если производная \(f'\) в точке \(x\) не существует и меняет свой знак слева направо с “\(+\)” на “\(-\)” (но \(x\) – внутренняя точка области определения функции \(f\,\)!), то эта точка является точкой максимума.
Пример: в точке \(A\) производная равна нулю и эта точка является точкой максимума; в точке \(C\) производная не “равна нулю”, а не существует, при этом точка \(C\) также является точкой максимума.
\(\blacktriangleright\) Если производная в точке \(x\) равна нулю и меняет свой знак слева направо с “\(-\)” на “\(+\)” , то эта точка является точкой минимума.
Также, если производная \(f'\) в точке \(x\) не существует и меняет свой знак слева направо с “\(-\)” на “\(+\)” (но \(x\) – внутренняя точка области определения функции \(f\,\)!), то эта точка является точкой минимума.
\(\blacktriangleright\) Заметим, что точки экстремума – это значение абсциссы \(x\).
\(\blacktriangleright\) Заметим, что существует такое понятие, как критические точки — это все точки, в которых производная функции либо равна нулю, либо не существует.
Таким образом, только часть критических точек является точками экстремума.
На рисунке изображен график производной функции \(f(x)\), определенной на отрезке \([-10;37]\). Найдите количество точек максимума функции \(f(x)\) на отрезке \([0;37]\).
Точка максимума – значение \(x\), в котором производная меняет свой знак с “\(+\)” на “\(-\)”. Следовательно, в этой точке ее график пересекает ось абсцисс “сверху вниз” (если двигаться по рисунку слева направо). Отметим отрезок \([0;37]\) и увидим, что таких точек 2:
Ответ: 2
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-2,4; 8,7)\). Найдите сумму точек экстремума этой функции на отрезке \([1;6]\).
Так как на рисунке изображен график функции, то точки экстремума – это точки на графике, в которых функция меняется с возрастания на убывание или наоборот. Эти точки: \(x=-1; \ 0; \ 2; \ 4; \ 5; \ 8.\) Из них на отрезке \([1;6]\) лежат только точки \(2; \ 4; \ 5\), следовательно, их сумма равна \(2+4+5=11.\)
Ответ: 11
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-3; 8,5)\). Найдите сумму точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция \(f(x)\) достигает локально минимальные значения в точках \(0\), \(4\) и \(8\), а локально максимальные значения в точках \(-2\), \(1\) и \(6\). Таким образом, сумма точек экстремума этой функции равна \(0 + 4 + 8 + (-2) + 1 + 6 = 17\).
Ответ: 17
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-2,4; 8,7)\). Найдите сумму точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция \(f(x)\) достигает локально минимальные значения в точках \(-1\), \(2\) и \(5\), а локально максимальные значения в точках \(0\), \(4\) и \(8\). Таким образом, сумма точек экстремума этой функции равна \(-1 + 2 + 5 + 0 + 4 + 8 = 18\).
Ответ: 18
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-3; 9)\). Найдите произведение точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция \(f(x)\) достигает локально минимальные значения в точках \(-1\) и \(5\), а локально максимальные значения в точках \(-2\), \(4\) и \(8\). Таким образом, произведение точек экстремума этой функции равно \((-1)\cdot 5\cdot (-2)\cdot 4\cdot 8 = 320\).
Ответ: 320
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-2.8; 7.8)\). Найдите произведение точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция \(f(x)\) достигает локально минимальные значения в точках \(1\) и \(4\), а локально максимальные значения в точках \(-2\), \(3\) и \(7\). Таким образом, произведение точек экстремума этой функции равно \(1\cdot 4\cdot (-2)\cdot 3\cdot 7 = -168\).
Ответ: -168
На рисунке изображен график \(y = f'(x)\) – производной функции \(y = f(x)\), определенной на интервале \((-1; 8)\). В какой точке отрезка \([2; 5]\) функция \(y = f(x)\) принимает наибольшее значение?
По рисунку можно определить, что функция \(y = f'(x)\) на отрезке \([2; 5]\) принимает неположительные значения, при этом \(f'(2) = 0\). Так как на полуинтервале \((2; 5]\) производная функции \(f(x)\) отрицательна, то сама функция \(f(x)\) на \((2; 5]\) убывает, тогда \(y = f(x)\) на отрезке \([2; 5]\) принимает наибольшее значение при \(x = 2\).
Ответ: 2
Итоговый экзамен по математике для выпускников 11-х классов обязательно включает задания на поиск точек максимума и минимума функциональных зависимостей. Их решение проводится аналитически – методом дифференцирования. Применение производной для исследования функции на экстремум сокращает время анализа и позволяет представить общий вид графика зависимости еще до выполнения построений.
Обучающий ресурс «Школково» позволит учащимся освежить в памяти главные моменты темы – уточнить теоретические знания и отработать их в решении ряда задач. Наш подход к обучению в отношении поиска точек экстремума функции через производную в типовых заданиях ЕГЭ основан на принципе глубокой взаимосвязи теории и практики. Сначала ученик читает правила «Теоретической справки», потом смотрит видео с объяснениями учителя, а затем работает с реальным педагогом. В процессе просмотра предлагаемых на сайте вебинаров можно задать интересующие вопросы и получить помощь в решении конкретных задач.
В разделе «Каталог» имеются подборки тематических заданий на нахождение точек экстремума функции с помощью производной, а также нахождения производной угла наклона касательной. Каждый пример содержит готовое решение и правильный ответ, с которыми можно ознакомиться после окончания самостоятельной работы. «Конструктор» примерных вариантов ЕГЭ позволит провести исследование экстремумов функций с помощью производных в ходе пробного выполнения экзаменационной работы.
