Тренировочные варианты «Школково». Досрочная волна. Реальные варианты ЕГЭ 2016

Во время распродажи пачка чипсов стоит \(170\cdot (1 - 0,2) = 136\) рублей. По условию задачи надо найти наибольшее целое число, при умножении которого на \(136\) результат останется не больше \(1100\). Это число получается после округления в меньшую сторону результата от деления \(1100\) на \(136\) и равно \(8\).

Ответ: 8

Двигатель разогрелся до температуры \(60^\circ F\) через \(3\) минуты после запуска, а до \(100^\circ F\) через \(8\) минут после начала запуска. От \(60^\circ F\) до \(100^\circ F\) двигатель разогревался \(8 - 3 = 5\,\)минут.

Ответ: 5

\[\mathrm{tg}\,(\beta - \alpha) = \dfrac{\mathrm{tg}\,\beta - \mathrm{tg}\,\alpha}{1 + \mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}\] Угол \(AOB\) можно представить в виде



\[\angle AOB = \beta - \alpha,\] тогда \[\mathrm{tg}\, AOB = \mathrm{tg}\,(\beta - \alpha) = \dfrac{\mathrm{tg}\,\beta - \mathrm{tg}\,\alpha}{1 + \mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta} = \dfrac{2 - \frac{1}{3}}{1 + \frac{1}{3}\cdot 2} = 1\,.\]

Ответ: 1

В среднем \(40 - 7 = 33\) шапки из сорока не имеют дефектов, следовательно, вероятность купить шапку без дефектов равна \[\dfrac{33}{40} = \dfrac{330}{400} = \dfrac{82,5}{100} = 0,825\,.\]

Ответ: 0,825

ОДЗ: \[13x - 13 > 0\qquad\Leftrightarrow\qquad x > 1\]

На ОДЗ: \[7^{\log_{49}(13x - 13)} = 7^{0,5\log_{7}(13x - 13)} = 7^{\log_{7}\sqrt{13x - 13}} = \sqrt{13x - 13},\] следовательно, на ОДЗ уравнение имеет вид: \[\sqrt{13x - 13} = 13\quad\Rightarrow\quad 13x - 13 = 13^2\quad\Rightarrow\quad 13x = 182\quad\Rightarrow\quad x = 14\] – подходит по ОДЗ.

Ответ: 14

Обозначим \(BC = x\), тогда \(AC = 2\sqrt{2}x\)

По теореме Пифагора:\[AB^2 = AC^2 + BC^2\qquad\Rightarrow\qquad 36 = 8x^2 + x^2\qquad\Rightarrow\qquad x^2 = 4,\] откуда \(x = 2\) (так как нас интересуют только \(x > 0\)).

Ответ: 2

В точке касания прямой \(y = 2x - 1\) и графика функции \(y = x^3 + 6x^2 + 11x - 1\) производная этой функции совпадает с угловым коэффициентом \(k\) прямой, который в данном случае равен \(2\).

Тогда \[y' = 2\ \Leftrightarrow\ 3x^2 + 12x + 11 = 2\ \Leftrightarrow\ 3x^2 + 12x + 9 = 0\ \Leftrightarrow\ x^2 + 4x + 3 = 0\] Корни последнего уравнения: \[x_1 = -3\qquad x_2 = -1\]

Проверим, при каком из полученных \(x\) прямая и график имеют общую точку:

при \(x = -3\):
ордината точки на прямой равна \(2\cdot(-3) - 1 = -7\), а ордината точки на графике равна \[(-3)^3 + 6\cdot(-3)^2 + 11\cdot(-3) - 1 = -7,\] то есть прямая и график проходят через точку \((-3; -7)\) и производная функции в точке \(x = -3\) совпадает с угловым коэффициентом прямой, следовательно, они касаются в этой точке.

при \(x = -1\):
ордината точки на прямой равна \(2\cdot(-1) - 1 = -3\), а ордината точки на графике равна \[(-1)^3 + 6\cdot(-1)^2 + 11\cdot(-1) - 1 = -7,\] то есть ординаты этих точек разные, следовательно, при \(x = -1\) у прямой и графика нет общей точки.

Итого: \(-3\) – искомая абсцисса.

Ответ: -3

Площадь поверхности данного многогранника равна площади поверхности прямоугольного параллелепипеда с измерениями \(10\times 12\times 13\) и равна таким образом \(2\cdot(10\cdot 12 + 12\cdot 13 + 10\cdot 13) = 812\).

Ответ: 812

Воспользуемся формулой косинуса двойного угла: \(\cos 2x = 1 - 2\sin^2x\), тогда при \(x = \dfrac{y}{2}\) имеем: \[\cos y = 1 - 2\sin^2\dfrac{y}{2}\qquad\Rightarrow\qquad \sin^2\dfrac{y}{2} = \dfrac{1 - \cos y}{2}\,.\]

Подставляя \(y = \dfrac{\pi}{6}\), получим: \[\sin^2\dfrac{\pi}{12} = \dfrac{1 - \cos \frac{\pi}{6}}{2} = \dfrac{1 - \frac{\sqrt{3}}{2}}{2}\,.\]

Так как \(\sqrt{48} = 4\sqrt{3}\), то исходное выражение можно переписать в виде \[4\sqrt{3}\cdot \dfrac{1 - \frac{\sqrt{3}}{2}}{2} - 2\sqrt{3} = 2\sqrt{3} - 3 - 2\sqrt{3} = -3\,.\]

Ответ: -3

По условию задачи имеем:\[Fl\cos\alpha\geqslant 9000\quad\Leftrightarrow\quad 120\cdot 150\cdot\cos\alpha\geqslant 9000\quad\Leftrightarrow\quad \cos\alpha\geqslant 0,5\,.\]

Учитывая, что \(\alpha\in[0^\circ; 90^\circ]\), получаем, что \(\alpha\leqslant 60^\circ\) (в этом легко убедиться, глядя на тригонометрический круг).

Таким образом, ответ: при \(\alpha = 60^\circ\).

Ответ: 60

Первый и второй насосы за минуту заполняют \(\dfrac{1}{9}\) часть бассейна,

второй и третий насосы за минуту заполняют \(\dfrac{1}{15}\) часть бассейна,

первый и третий насосы за минуту заполняют \(\dfrac{1}{10}\) часть бассейна, тогда \[\dfrac{1}{9} + \dfrac{1}{15} + \dfrac{1}{10} = \dfrac{25}{90}\] – часть бассейна, заполняемая за минуту всеми тремя насосами, если вклад каждого насоса учесть дважды. Тогда \[\dfrac{1}{2}\cdot\dfrac{25}{90} = \dfrac{25}{180}\] – часть бассейна, заполняемая за минуту всеми тремя насосами.

Следовательно, все три насоса заполняют бассейн за \(\dfrac{180}{25} = 7,2\) минуты.

Ответ: 7,2

ОДЗ: \[121x > 0\qquad\Leftrightarrow\qquad x > 0\] Решим на ОДЗ:

1) \[y' = 121 - \dfrac{121}{121x} = 121 - \dfrac{1}{x} = \dfrac{121x - 1}{x}\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{121x - 1}{x} = 0\qquad\Leftrightarrow\qquad x = \dfrac{1}{121}\]

Производная функции \(y\) не существует при \(x = 0\), но \(x = 0\) не входит в ОДЗ. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):

3) Найдём промежутки знакопостоянства \(y'\) на рассматриваемом отрезке \(\left[\dfrac{1}{242}; \dfrac{5}{242}\right]\):

4) Эскиз графика на отрезке \(\left[\dfrac{1}{242}; \dfrac{5}{242}\right]\):

Таким образом, наименьшее значение на отрезке \(\left[\dfrac{1}{242}; \dfrac{5}{242}\right]\) функция \(y\) достигает в \(x = \dfrac{1}{121}\):

\[y\left(\dfrac{1}{121}\right) = \dfrac{121}{121} - \ln\dfrac{121}{121} + 3 = 1 - 0 + 3 = 4\,.\]

Итого: \(4\) – наименьшее значение функции \(y\) на отрезке \(\left[\dfrac{1}{242}; \dfrac{5}{242}\right]\).

Ответ: 4

а) ОДЗ: \[\cos x\neq 0\qquad\Leftrightarrow\qquad x \neq \dfrac{\pi}{2} + \pi k,\ k\in\mathbb{Z}\]

На ОДЗ: \[\cos x(2\cos x + \mathrm{tg}\, x) = 1\quad\Leftrightarrow\quad 2\cos^2 x + \sin x = 1\quad\Leftrightarrow\quad 2 - 2\sin^2 x + \sin x = 1\]

Сделаем замену \(t = \sin x\): \[2 - 2t^2 + t = 1\quad\Leftrightarrow\quad 2t^2 - t - 1 = 0\]

Корни последнего уравнения:\[t_1 = 1,\qquad t_2 = -\dfrac{1}{2}\,,\] откуда \(\sin x = 1\) или \(\sin x = -\dfrac{1}{2}\)

1) \(\sin x = 1\), следовательно, \(x = \dfrac{\pi}{2} + 2\pi n\) – не подходят по ОДЗ.

2) \(\sin x = -\dfrac{1}{2}\)



откуда \(x_1 = -\dfrac{\pi}{6} + 2\pi k\), \(x_2 = \dfrac{7\pi}{6} + 2\pi k\), \(k\in\mathbb{Z}\) – подходят по ОДЗ.

б) \(-\pi \leqslant -\dfrac{\pi}{6} + 2\pi k \leqslant \dfrac{\pi}{2}\) равносильно \(-\dfrac{5\pi}{6} \leqslant 2\pi k \leqslant \dfrac{4\pi}{6}\), что равносильно \(-\dfrac{5}{12} \leqslant k \leqslant \dfrac{1}{3}\), но \(k\in\mathbb{Z}\), следовательно, среди этих решений подходит только решение при \(k = 0\): \(x = -\dfrac{\pi}{6}\)

\(-\pi \leqslant \dfrac{7\pi}{6} + 2\pi k \leqslant \dfrac{\pi}{2}\) равносильно \(-\dfrac{13\pi}{6} \leqslant 2\pi k \leqslant -\dfrac{4\pi}{6}\), что равносильно \(-\dfrac{13}{12} \leqslant k \leqslant -\dfrac{1}{3}\), но \(k\in\mathbb{Z}\), следовательно, среди этих решений подходит только решение при \(k = -1\): \(x = -\dfrac{5\pi}{6}\).

Ответ:

а) \(-\dfrac{\pi}{6} + 2\pi k, \dfrac{7\pi}{6} + 2\pi k, k\in\mathbb{Z}\)

б) \(-\dfrac{\pi}{6}, -\dfrac{5\pi}{6}\)

а) Т.к. призма правильная, то она прямая и в основании ее лежит квадрат \(ABCD\).

Обозначим \(AM=x\), тогда \(MA_1=3x\). Т.к. \(\alpha\parallel AC\), то \(\alpha\) пересечет плоскость \(ACC_1\), в которой лежит прямая \(AC\), по прямой \(MK\), параллельной \(AC\). Значит, \(CK=x, KC_1=3x\).

Необходимо доказать, что точка \(N\) – середина \(DD_1\).

Пусть \(MK\cap BN=O\), \(AC\cap BD=Q\). Плоскости \(BDD_1\) и \(ACC_1\) пересекаются по прямой \(QQ_1\), проходящей через точки пересечения диагоналей граней \(ABCD\) и \(A_1B_1C_1D_1\) и параллельной \(AA_1\). Т.к. \(BN\in BDD_1\), \(MK\in ACC_1\), то точка \(O\) лежит на \(QQ_1\), следовательно, \(OQ\parallel AA_1 \Rightarrow OQ\perp (ABC)\). Таким образом, \(OQ=AM=x\).

\(\triangle OQB\sim \triangle NDB\) по двум углам (\(\angle D=\angle Q=90^\circ, \angle B\) – общий), следовательно,

\[\dfrac{ND}{OQ}=\dfrac{DB}{QB} \Leftrightarrow \dfrac{ND}x= \dfrac{2QB}{QB} \Rightarrow ND=2x\]

Но все ребро \(DD_1=AA_1=4x\), следовательно, \(N\) – середина \(DD_1\).

б) По теореме о трех перпендикулярах (\(OQ\perp (ABC), \text{проекция } BQ\perp AC\)) наклонная \(BO\perp AC \Rightarrow BO\perp MK\) (т.к. \(AC\parallel MK\)). Значит, \(BN\perp MK\).

Площадь выпуклого четырехугольника, диагонали которого взаимно перпендикулярны, равна полупроизведению диагоналей, то есть \(S_{MBKN}=\dfrac 12 MK\cdot BN\). Найдем \(MK\) и \(BN\).

\(MK=AC=AB\sqrt 2=5\sqrt2\).

По теореме Пифагора \(BN=\sqrt{BD^2+ND^2}=\sqrt{(5\sqrt2)^2+4^2}=\sqrt{66}\)

Значит, \(S_{MBKN}=\dfrac12\cdot 5\sqrt2\cdot \sqrt{66}=5\sqrt{33}\).

Ответ:

б) \(5\sqrt{33}\)

ОДЗ:

\[\begin{aligned} \begin{cases} x > 0\\ x\neq 1\\ x^2 + 4x - 5\geqslant 0\\ \sqrt{x^2 + 4x - 5} + 3 > 0\\ x^2 + 4x - 4 > 0 \end{cases} \qquad\Leftrightarrow\qquad x > 1 \end{aligned}\]

На ОДЗ:
\(\log_x 6 > 0\), следовательно, исходное неравенство равносильно неравенству

\[\begin{aligned} &\dfrac{\log_x(\sqrt{x^2 + 4x - 5} + 3)}{\log_x 6}\cdot\lg(x^2 + 4x - 4)\geqslant 1\qquad\Leftrightarrow\\ \Leftrightarrow\qquad &\log_6(\sqrt{x^2 + 4x - 5} + 3)\cdot\lg(x^2 + 4x - 4)\geqslant 1 \end{aligned}\]

Сделаем замену \(t = \sqrt{x^2 + 4x - 5} > 0\).

После замены: \[\log_6(t + 3)\cdot\lg(t^2 + 1)\geqslant 1\]

При \(t > 0\) оба множителя в левой части возрастают, следовательно, их произведение возрастает, а правая часть постоянна, тогда равенство \[\log_6(t + 3)\cdot\lg(t^2 + 1) = 1\] может достигаться только в одной точке. Легко убедиться, что оно выполнено при \(t = 3\), следовательно, только при \(t\geqslant 3\) будет выполнено последнее неравенство.

Таким образом, \[\sqrt{x^2 + 4x - 5}\geqslant 3,\] что на ОДЗ равносильно \[x^2 + 4x - 5\geqslant 9\quad\Leftrightarrow\quad x^2 + 4x - 14\geqslant 0\quad\Leftrightarrow\quad (x + 2 - 3\sqrt{2})(x + 2 + 3\sqrt{2})\geqslant 0,\] откуда с учётом ОДЗ \[x\in[3\sqrt{2} - 2; +\infty)\,.\]

Ответ:

\([3\sqrt{2} - 2; +\infty)\)

а) По теореме об отрезках касательной \(AN = NB\), \(AM = MC\), \(BK = KC\), тогда

\[\begin{aligned} &\dfrac{MN + NK - MK}{2} = \dfrac{AM + AN + NB + BK - MC - KC}{2} =\\ = \,&\dfrac{MC + NB + NB + BK - MC - BK}{2} = NB, \end{aligned}\]

что и требовалось доказать.

б) Обозначим \(MA = ka\), \(AN = a\) (тогда искомая величина есть \(k\)), следовательно \(NB = a\), тогда \(BK = 2a\).

По теореме об отрезках касательной: \[MC = ka,\qquad CK = 2a.\]

Запишем теорему косинусов для треугольника \(MNK\): \[MK^2 = MN^2 + NK^2 - 2\cdot MN\cdot NK\cdot\cos\angle MNK\,.\] Подставляя известные величины, получим:

\[\begin{aligned} &(ka + 2a)^2 = (ka + a)^2 + 9a^2 - 2\cdot (ka + a)\cdot 3a\cdot 0,5\quad\Leftrightarrow\\ \Leftrightarrow\quad &a^2(k + 2)^2 = a^2(k + 1)^2 + 9a^2 - (k + 1)\cdot 3a^2\quad\Leftrightarrow\\ \Leftrightarrow\quad &(k + 2)^2 = (k + 1)^2 + 9 - 3(k + 1)\quad\Leftrightarrow\quad 5k = 3\quad\Leftrightarrow\quad k = 0,6\,. \end{aligned}\]

Ответ:

б) \(0,6\)

По первой схеме Тимуру придётся выплатить \((1 + 1,8)\cdot 600 = 1680\) млн. руб. за 40 лет. Таким образом, в месяц Тимуру придётся выплачивать \[\dfrac{1680}{40\cdot 12} = 3,5\ \text{млн. руб.}\]

Тогда по второй схеме Тимур сможет откладывать по \(3,5 - 1 = 2,5\) млн. руб. в месяц, следовательно, ему понадобится \[\dfrac{600\ \text{млн. руб.}}{2,5\ \text{млн. руб./месяц}} = 240\ \text{месяцев},\] что составляет \(20\) лет.

Ответ:

\(20\) лет

Условие данной задачи можно переформулировать следующим образом: при каких \(a\) существует хотя бы одна точка на графике функции \(y\), которая находится ниже прямой \(y=4\), или, что то же самое:

\[3\cdot|2x + a| + 2\cdot|x^2 - x - 2|<4 \quad \text{ имеет хотя бы одно решение.}\]

Сделаем замену \(-\frac12 a=b\). Тогда неравенство перепишется в виде:

\[6|x-b|+2|x^2-x-2|<4 \quad \Leftrightarrow \quad |x^2-x-2|<2-3|x-b|\]

Рассмотрим две функции: \(f(x)=|x^2-x-2|\) и \(g(x)=2-3|x-b|\). График функции \(g(x)\) при каждом фиксированном \(b\) представляет собой угол, ветви которого направлены вниз, а вершина находится в точке \((b;2)\).

Тогда смысл неравенства таков: необходимо найти те значения \(b\), при которых существует хотя бы одна точка \(X\) графика \(f(x)\), находящаяся ниже графика функции \(g(x)\).

Найдем те значения \(b\), когда не существует таких точек \(X\): то есть когда все точки графика \(f(x)\) находятся не ниже точек графика \(g(x)\). Тогда в ответ пойдут все значения \(b\), кроме найденных.

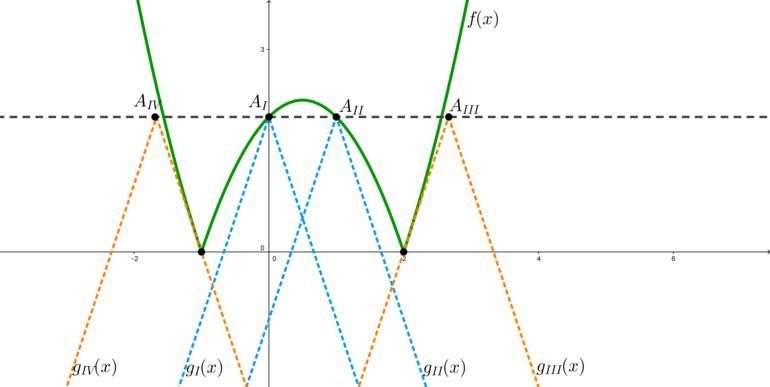
1) Рассмотрим значения \(b\), при которых вершина угла находится между точкой \(A_I\) и точкой \(A_{II}\) (включая эти точки). В этом случае все точки графика \(f(x)\) находятся не ниже точек графика \(g(x)\). Найдем эти значения \(b\):

точка \(A_I\) имеет координаты \((0;2)\), следовательно, \(b=0\); точка \(A_{II}\) имеет координаты \((1;2)\), следовательно, \(b=1\). Значит, при всех \(b\in [0;1]\) все точки графика \(f(x)\) не ниже точек графика \(g(x)\).

Заметим, что когда вершина угла находится между точками \(A_{II}\) и \(A_{III}\), то всегда есть хотя бы одна точка графика \(f(x)\), находящаяся ниже графика \(g(x)\).

2) Так происходит до тех пор, пока вершина не будет в точке \(A_{III}\) — когда левая ветвь \(g(x)\) касается правой ветви \(f(x)\) в точке \(x_0\); и в этом случае снова все точки графика \(f(x)\) находятся не ниже \(g(x)\). Найдем это значение \(b\).

Правая ветвь \(f(x)\) задается уравнением \(y=x^2-x-2, x\geqslant 2\); левая ветвь \(g(x)\) задается уравнением \(y_1=2+3(x-b), x\leqslant b\).

\((x^2-x-2)'=2x-1, \quad 2x_0-1=3 \Rightarrow x_0=2 \Rightarrow y(2)=y_1(2) \Rightarrow b=\dfrac83\).

Значит, при всех \(b\geqslant \dfrac83\) все точки графика \(f(x)\) будут находиться не ниже точек графика \(g(x)\).

3) Аналогично рассматривается случай, когда вершина угла находится в точке \(A_{IV}\) или левее (правая ветвь \(g(x)\) касается левой ветви \(f(x)\)). В этом случае \(b\leqslant -\dfrac53\).

Таким образом, мы нашли значения \(b\), когда все точки графика \(f(x)\) будут находиться не ниже точек графика \(g(x)\). Значит, в ответ должны пойти все значения \(b\), кроме найденных, а это: \(b\in \left(-\dfrac53; 0\right)\cup \left(1; \dfrac83\right)\).

Перейдем теперь к \(a\): т.к. \(b=-\frac12 a\), то \(a\in \left(-\dfrac{16}3; -2\right)\cup\left(0;\dfrac{10}3\right)\).

Ответ:

\(a\in \left(-\dfrac{16}3; -2\right)\cup\left(0;\dfrac{10}3\right)\)

а) Такое возможно, например, в случае, если в классе \(25\) учеников и \(12\) из них слышали первую строчку до перемены.

б) Такое возможно, например, в случае, если в классе \(28\) учеников и \(7\) из них слышали первую строчку до перемены – тогда до перемены первую строчку слышали или видели \[\dfrac{7}{28}\cdot 100\% = 25\%\ \text{учеников,}\] а после перемены \[\dfrac{8}{28}\cdot 100\% = \dfrac{200}{7}\%\ \text{учеников.}\]

в) В случае, если в классе \(25\) человек и в итоге первую строчку этого стихотворения услышал/увидел только один человек, процент учеников класса, так и не услышавших и не увидевших первой строчки этого стихотворения равен \[\dfrac{24}{25}\cdot 100 = 96\,.\]

Докажем, что большего целого значения эта величина принять не могла. В самом деле, если процент учеников, не слышавших и не видевших первую строчку – целое число, то и процент учеников, слышавших/видевших первую строчку тоже целое число.

Понятно также, что процент учеников, не слышавших и не видевших первую строчку, максимален тогда и только тогда, когда минимален процент учеников, слышавших/видевших первую строчку.

Сделать процент учеников, слышавших/видевших первую строчку, ещё меньше можно только в случае, когда ровно один ученик слышал/видел первую строчку, а в классе количество учеников больше, чем \(25\). Пусть в классе \(u > 25\) учеников, тогда искомый процент равен \[\dfrac{1}{u}\cdot 100\,.\]

Мы доказали, что это число должно быть целым, чтобы выполнилось условие задачи, но тогда \(100\) должно делиться на \(u\), где \(25 < u\leqslant 35\) – целое. Легко убедиться, что подходящих \(u\) нет, следовательно, окончательный ответ: \(96\).

Ответ:

а) Да

б) Да

в) \(96\)