3. Геометрия на плоскости (планиметрия). Часть I
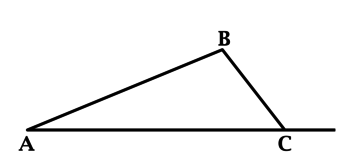
В треугольнике \(ABC\): \(\angle B = 81^{\circ}\), \(\angle C = 25^{\circ}\). Найдите внешний угол при вершине \(A\). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, \(\angle B + \angle C =\) внешнему углу при вершине \(A\), следовательно \(A_{\text{внеш}}\) \( = 81^{\circ} + 25^{\circ} = 106^{\circ}\).
Ответ: 106
В треугольнике \(ABC\): \(\angle A = 22^{\circ}\), внешний угол при вершине \(C\) равен \(130^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, \(\angle A + \angle B = C_{\text{внеш}}\), тогда \(22^{\circ} + \angle B = 130^{\circ}\), откуда находим \(\angle B = 130^{\circ} - 22^{\circ} = 108^{\circ}\).
Ответ: 108
В треугольнике \(ABC\): \(\angle C = 35^{\circ}\), внешний угол при вершине \(B\) равен \(91^{\circ}\). Найдите \(\angle A\). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, \(\angle C + \angle A = B_{\text{внеш}}\), тогда \(35^{\circ} + \angle A = 91^{\circ}\), откуда находим \(\angle A = 91^{\circ} - 35^{\circ} = 56^{\circ}\).
Ответ: 56
В треугольнике \(ABC\): \(\angle C = 70^{\circ}\), \(AB = BC\). Найдите \(\angle B\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C = 70^{\circ}\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ}\).
Ответ: 40
В треугольнике \(ABC\): \(\angle A = 47^{\circ}\), \(AB = BC\). Найдите \(\angle B\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle C = \angle A = 47^{\circ}\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - 47^{\circ} - 47^{\circ} = 86^{\circ}\).
Ответ: 86
В треугольнике \(ABC\): \(\angle C = 36^{\circ}\), \(AB = BC\). Найдите \(\angle B\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C = 36^{\circ}\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}\).
Ответ: 108
В треугольнике \(ABC\): \(\angle B = 38^{\circ}\), \(AB = BC\). Найдите \(\angle C\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 38^{\circ} + \angle A + \angle C = 38^{\circ} + 2\cdot \angle A\), откуда \(2\cdot \angle A = 142^{\circ}\), тогда \(\angle A = 71^{\circ}\).
Ответ: 71
