\(\blacktriangleright\) Сложная функция (композиция двух функций) — это функция \(f=f(x)\), представимая в виде \(f=f(t(x))\), где \(t=t(x)\) – функция, являющаяся “новой переменной” для функции \(f\).
То есть в такой функции можно ввести новую переменную \(t\) так, что функция полностью будет зависеть от этой новой переменной.
\(\blacktriangleright\) Производная такой функции ищется по правилу: \[{\Large{f'(x)=f'(t)\cdot t'(x)}}\]
Примеры:
\(1)\) Функция \(f(x)=\cos {(x^2+1)}\). Если сделать замену \(t(x)=x^2+1\), то функция примет вид \(f(t)=\cos t\).
Найдем \(f'(t)=(\cos t)'=-\sin t=(\text{переход к переменной
}x)=-\sin
{(x^2+1)}\)
Найдем \(t'(x)=(x^2+1)'=2x\)
Значит, \(f'(x)=-2x\cdot \sin{(x^2+1)}\)
\(2)\) Функция \(f(x)=x^3 +x^2\). Для этой функции не существует никакой замены, кроме тождественной (\(t(x)=x\)). Значит она – не сложная.
Ее производную можно найти обычным способом, т.к. она элементарная:
\(f'(x)=3x^2+2x\)
\(3)\) Функция \(f(x)=\sin x^2 + x\). Для этой функции не существует никакой замены, кроме тождественной (\(t(x)=x\)).
Но обычными способами вычислить ее производную не удастся. Заметим, что эта функция представлена в виде суммы двух, причем одна из них сложная (\(g(x)=\sin x^2\)), а другая – элементарная (\(h(x)=x\)).
Т.к. мы знаем, что \(f'=g'+h'\), то найдем в отдельности производные функций \(g\) и \(h\).
Тогда \(f'(x)=2x\cdot \cos x^2 + 1\)
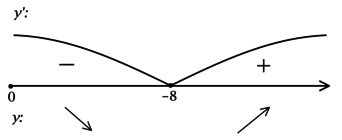
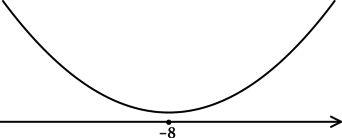
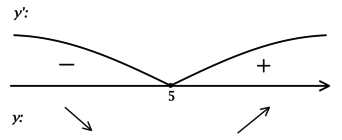
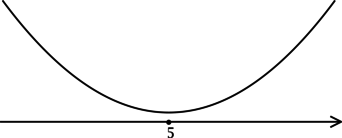
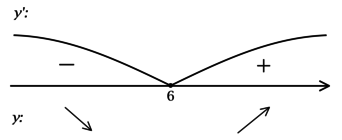
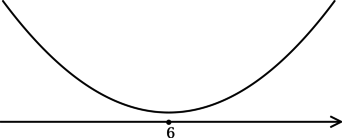
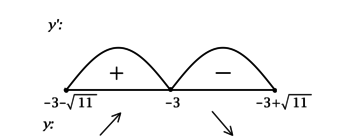
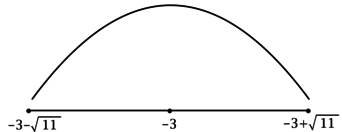
\(\blacktriangleright\) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания (\(f'>0\)) и убывания (\(f'<0\)) функции, критические точки (где \(f'=0\) или \(f'\) не существует).
\[\begin{array}{|r|c|c|}
\hline & \text{Функция } f(x) & \text{Производная } f'(x)\\
\hline
\textbf{1} & c & 0\\&&\\
\textbf{2} & x^a & a\cdot x^{a-1}\\&&\\
\textbf{3} & \ln x & \dfrac1x\\&&\\
\textbf{4} & \log_ax & \dfrac1{x\cdot \ln a}\\&&\\
\textbf{5} & e^x & e^x\\&&\\
\textbf{6} & a^x & a^x\cdot \ln a\\&&\\
\textbf{7} & \sin x & \cos x\\&&\\
\textbf{8} & \cos x & -\sin x\\[1ex]
\hline
\end{array} \quad \quad \quad \quad
\begin{array}{|r|c|c|}
\hline & \text{Функция } f(x) & \text{Производная } f'(x)\\
\hline
\textbf{9} & \mathrm{tg}\, x & \dfrac1{\cos^2 x}\\&&\\
\textbf{10} & \mathrm{ctg}\, x & -\,\dfrac1{\sin^2 x}\\&&\\
\textbf{11} & \arcsin x & \dfrac1{\sqrt{1-x^2}}\\&&\\
\textbf{12} & \arccos x & -\,\dfrac1{\sqrt{1-x^2}}\\&&\\
\textbf{13} & \mathrm{arctg}\, x & \dfrac1{1+x^2}\\&&\\
\textbf{14} & \mathrm{arcctg}\, x & -\,\dfrac1{1+x^2}\\[0.5ex]
\hline
\end{array}\]