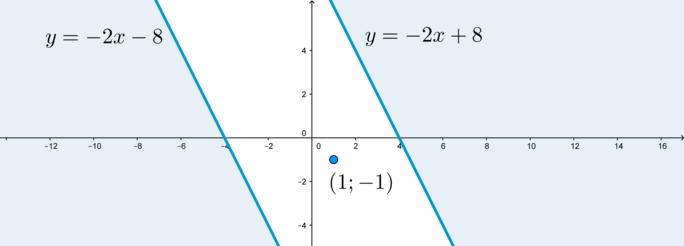Найдите все значения \(a\), при каждом из которых система уравнений \[\begin{cases} x(x^2+y^2-2y-8)=|x|\cdot (2y-8)\\ y=x+a \end{cases}\]
имеет ровно три решения.
(Задача от подписчиков)
1) Изобразим график первого уравнения.
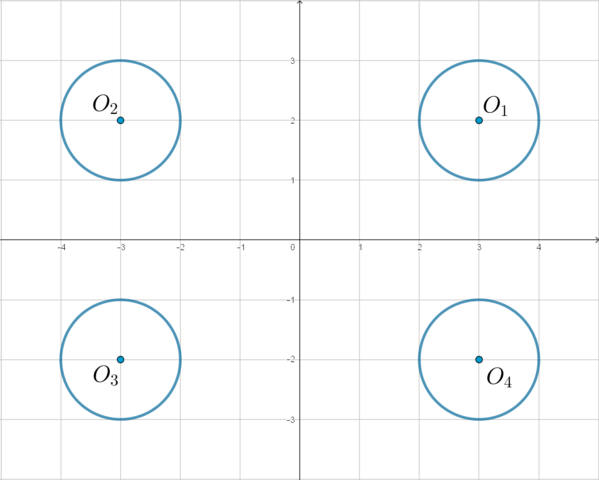
а) При \(x>0\) уравнение принимает вид: \[x(x^2+y^2-2y-8)=x(2y-8) \quad\Rightarrow\quad x^2+(y-2)^2=4\] Мы получили уравнение окружности (назовем ее \(s\)) с центром в точке \((0;2)\) и радиусом \(2\).
б) При \(x=0\) уравнение принимает вид: \[0\cdot (0+y^2-2y-8)=0\cdot (2y-8) \quad\Rightarrow\quad 0=0\] Таким образом, мы получили верное равенство. Следовательно, мы получили множество точек, абсцисса \(x\) которых равна нулю.
в) При \(x<0\) уравнение принимает вид: \[x(x^2+y^2-2y-8)=-x(2y-8) \quad\Rightarrow\quad x^2+y^2=16\] Мы получили уравнение окружности (назовем ее \(S\)) с центром в точке \((0;0)\) и радиусом \(4\).
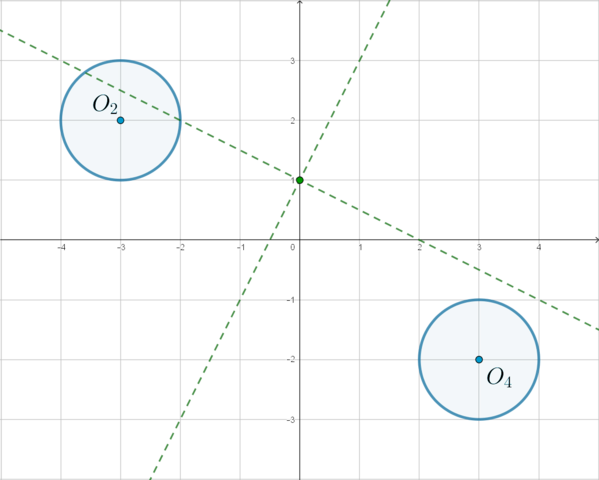
2) Уравнение \(y=x+a\) задает множество прямых, параллельных прямой \(y=x\) (это прямые, угол наклона которых к положительному направлению оси \(Ox\) равен \(45^\circ\)).
Таким образом, получаем такую картинку (голубым цветом изображен график первого уравнения):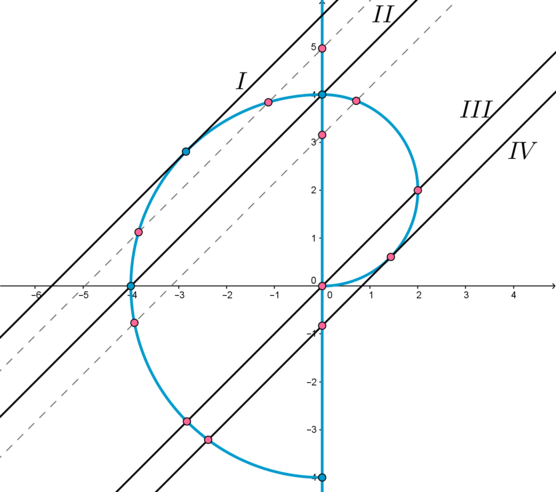
3) Для того, чтобы система имела 3 решения, нужно, чтобы при некотором фиксированном \(a\) прямая \(y=x+a\) пересекала “голубой график” ровно в трех точках.
Таким образом, нам подходят следующие случаи:
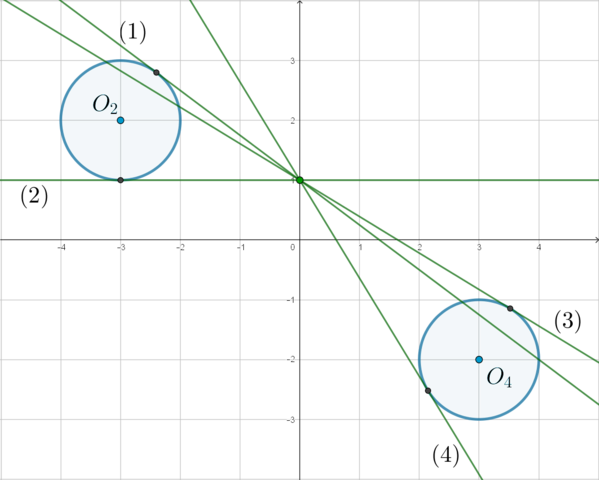
— когда прямая \(y\) находится между \(I\) и \(II\) (не включая эти случаи). Случай \(I\) – касание прямой \(y\) и окружности \(S\). Случай \(II\) – прохождение прямой \(y\) через точку пересечения окружности \(S\) и прямой \(x=0\).
— когда прямая \(y\) находится между \(II\) и \(III\) (не включая \(II\) и включая \(III\)). Случай \(III\) – прохождение прямой \(y\) через точку пересечения окружности \(s\) и прямой \(x=0\).
— когда прямая \(y\) находится в положении \(IV\) – касается окружности \(s\).
Рассмотрим каждый из этих случаев по отдельности.
Между \(I\) и \(II\).
– Найдем значение \(a\), при котором прямая \(y\) находится в положении \(I\). В этом случае \(a>0\).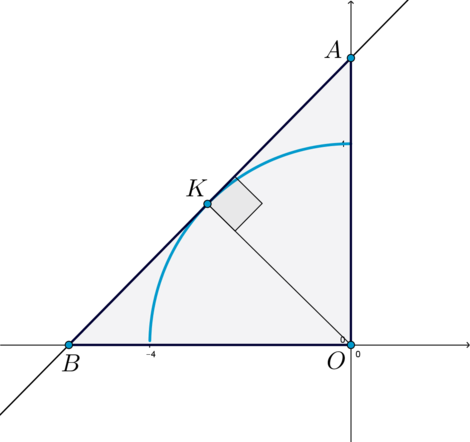
Пусть \(A(0;a), \ B(-a;0)\) – точки пересечения \(y\) с осями координат, \(K\) – точка касания. Тогда \(OK\perp AB\) (как радиус, проведенный в точку касания). Длина \(OA=a\), \(OB=a\), \(OK=4\), \(\triangle AOB\) прямоугольный. Тогда \(AB=a\sqrt2\). Тогда \[S_{\triangle AOB}=\dfrac12 OK\cdot AB=\dfrac12 OB\cdot OA
\quad\Rightarrow\quad a=4\sqrt2.\] – Найдем значение \(a\), при котором прямая \(y\) находится в положении \(II\). В этом случае \(y\) проходит через точку \((0;4)\), следовательно, \[4=0+a \quad\Rightarrow\quad a=4\]
Таким образом, нам подходят значения \(a\in (4;4\sqrt2)\).
Между \(II\) и \(III\).
– Найдем \(a\), при котором прямая \(y\) находится в положении \(III\). В этом случае она проходит через точку \((0;0)\), то есть \(a=0\).
Таким образом, нам подходят \(a\in [0;4)\).
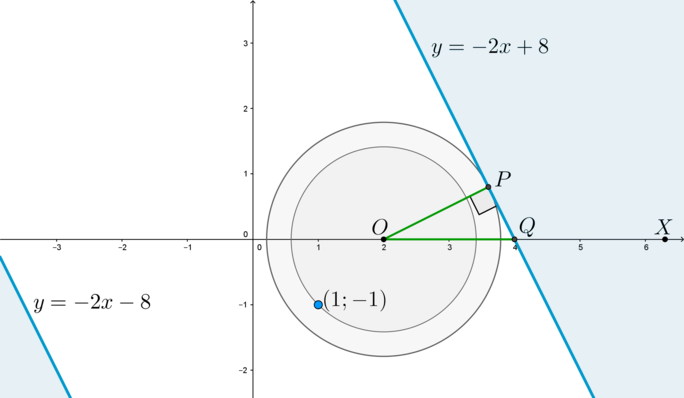
Положение \(IV\).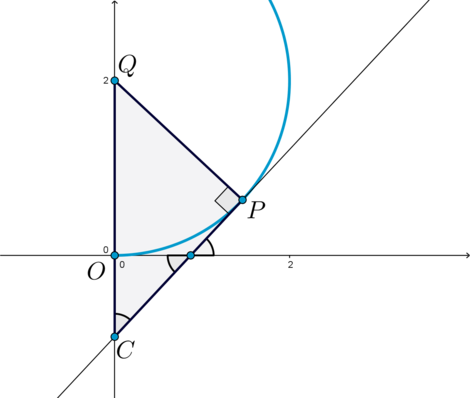
В этом случае \(a<0\). Пусть \(Q\) – центр окружности \(s\), \(P\) – точка касания, \(C\) – точка пересечения \(y\) с осью ординат. Тогда \(\triangle QPC\) – прямоугольный. Ранее мы говорили, что прямая \(y\) наклонена к положительному направлению оси \(Ox\) под углом \(45^\circ\), откуда будет следовать, что и \(\angle QCP=45^\circ\). Радиус \(QP=2\), отрезок \(OC=-a\) (так как \(a<0\)), \(QO=2\). Следовательно, \[\sin\angle QCP=\sin 45^\circ=\dfrac{\sqrt2}2=\dfrac{QP}{QC}=
\dfrac{2}{2-a}
\quad\Rightarrow\quad a=-2\sqrt2+2.\]
Таким образом, обобщая все решение, находим ответ: \[a\in \{-2\sqrt2+2\}\cup[0;4)\cup(4;4\sqrt2).\]
Ответ:
\(\{-2\sqrt2+2\}\cup[0;4)\cup(4;4\sqrt2)\)