Найдите площадь квадрата \(ABCD\), если \(AC = 10\).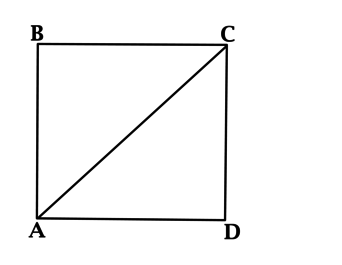
\(AD = CD\); по теореме Пифагора находим: \(AС^2 = AD^2 + CD^2 = 2\cdot AD^2\), тогда \(AD^2 = 50\), но площадь квадрата \(ABCD\) и равна \(AD^2\).
Ответ: 50
3. Геометрия на плоскости (планиметрия). Часть I
Сумма внутренних углов любого четырехугольника равна \(360^\circ\).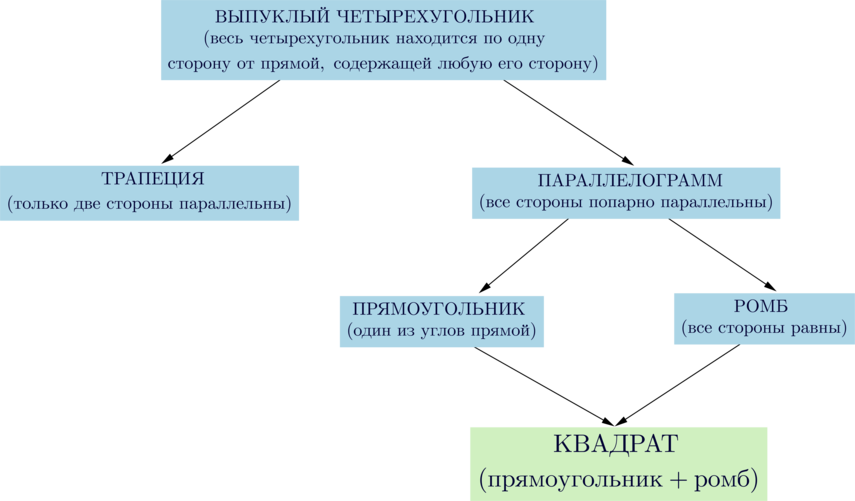
Свойства квадрата:
\(\blacktriangleright\) Те же, что и у ромба и прямоугольника:
\(\sim\) Все стороны равны;
\(\sim\) Диагонали точкой пересечения делятся пополам;
\(\sim\) Все углы прямые;
\(\sim\) Диагонали взаимно перпендикулярны и являются биссектрисами углов квадрата;
\(\sim\) Диагонали равны.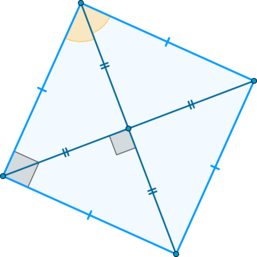
Площадь квадрата
1. Т.к. квадрат является ромбом, то его площадь также равна половине произведения диагоналей.
2. Площадь квадрата равна квадрату его стороны.
Найдите площадь квадрата \(ABCD\), если \(AC = 10\).
\(AD = CD\); по теореме Пифагора находим: \(AС^2 = AD^2 + CD^2 = 2\cdot AD^2\), тогда \(AD^2 = 50\), но площадь квадрата \(ABCD\) и равна \(AD^2\).
Ответ: 50
В квадрате \(ABCD\) расстояние от точки пересечения диагоналей до одной из его сторон равно \(5\). Найдите площадь этого квадрата.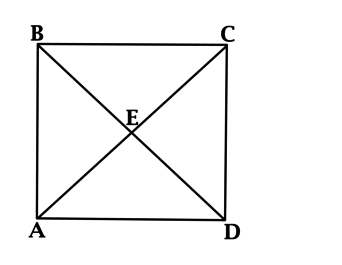
Пусть \(E\) – точка пересечения диагоналей квадрата \(ABCD\).
В квадрате диагонали равны, пересекаются и точкой пересечения делятся пополам, тогда \(AE = ED\) и \(\angle DAE = \angle EDA\).
Так как квадрат является и ромбом, то в квадрате диагонали делят углы пополам, тогда \(\angle DAE = 0,5 \cdot 90^{\circ} = 45^{\circ}\), тогда \(\angle AED = 180^{\circ} - 45^{\circ} - 45^{\circ} = 90^{\circ}\).
В треугольнике \(ADE\) опустим из \(E\) высоту \(EF\) на \(AD\) (длина \(EF\) и есть расстояние от точки \(E\) до стороны). Так как \(AE = ED\), то \(EF\) является и медианой, но в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(EF = 0,5\cdot AD\).
Аналогично остальные расстояния от \(E\) до сторон квадрата равны половине стороны квадрата, тогда \(AD = 10\), следовательно, площадь квадрата \(ABCD\) равна 100.
Ответ: 100
Сумма диагоналей квадрата равна \(2\sqrt2\). Найдите его периметр.

Если сумма диагоналей равна \(2\sqrt2\), а диагонали квадрата равны, то одна диагональ равна \(\sqrt2\). Т.к. диагональ квадрата в \(\sqrt2\) раз больше стороны, то сторона равна \(1\) \(\Rightarrow\) периметр равен \(4\).
Ответ: 4
Сумма диагоналей квадрата равна \(4\). Найдите его площадь.

Если сумма диагоналей равна \(4\), а диагонали квадрата равны, то каждая диагональ равна \(2\). Так как площадь квадрата, как и ромба, равна полупроизведению диагоналей, то площадь равна \(\frac{1}{2}\cdot2\cdot2 = 2\).
Ответ: 2
Периметр квадрата равен \(2\). Найдите его площадь.

Сторона квадрата равна \(2:4 = 0,5\) \(\Rightarrow\) его площадь равна \(0,5\cdot0,5 = 0,25\).
Ответ: 0,25
Площадь квадрата равна \(1\). Найдите его периметр.

Пусть \(AB=x\) – сторона квадрата, тогда \(x^2 = 1\) \(\Rightarrow\) \(x =
1\). Периметр квадрата равен \(4\cdot x = 4\cdot1 = 4\).
Ответ: 4
В квадрате \(ABCD\) расстояние от середины \(AB\) до середины \(AD\) равно \(3\). Найдите площадь квадрата \(ABCD\).
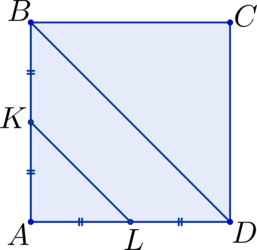
Отрезок \(KL\), соединяющий середины \(AB\) и \(AD\), является средней линией в \(\triangle ABD\) \(\Rightarrow\) \(2\cdot KL = BD\) \(\Rightarrow\) диагональ \(BD = 6 = AC\) \(\Rightarrow\) \(S_{ABCD} = \frac{1}{2}\cdot6\cdot6 = 18\).
Ответ: 18
Планиметрические задачи на тему «Квадрат» в ЕГЭ по математике включаются каждый год. Это означает, что справляться с ними должны уметь все учащиеся, независимо от того, базовый или профильный уровень экзамена они планируют сдавать. Освоив задания по теме «Квадрат», учащиеся смогут успешно выполнить ЕГЭ по математике и рассчитывать на получение конкурентных баллов по итогам прохождения аттестационного испытания.
Чтобы задачи ЕГЭ по теме «Квадрат» не вызывали сложностей, рекомендуем вспомнить основные свойства этой фигуры, а также формулу нахождения ее площади. Вся базовая информация, которая поможет выпускникам качественно подготовиться к экзамену, опубликована на образовательном портале «Школково». Наши специалисты подготовили материал и представили его в максимально доступной форме. Ознакомиться с ним можно в разделе «Теоретическая справка».
Чтобы закрепить усвоенный материал и научиться справляться с задачами ЕГЭ на нахождение площади квадрата, выпускники могут прорешать упражнения по данной теме. Большая подборка подобных заданий с подробным описанием алгоритма нахождения правильного ответа представлена в разделе «Каталог». База упражнений «Школково» постоянно обновляется.
Попрактиковаться в выполнении заданий по данной теме или, например, в решении задач на тему «Трапеция» школьники могут в онлайн-режиме, находясь в Москве или любом другом российском городе.
© 2024 Все права защищены | Карта сайта
Политика конфиденциальности
Пользовательское соглашение
