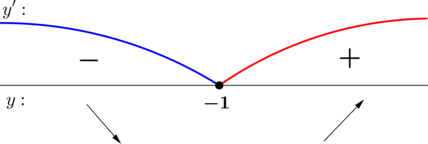
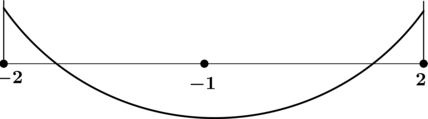
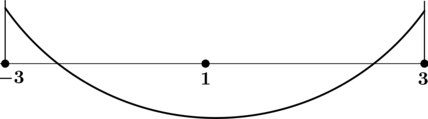
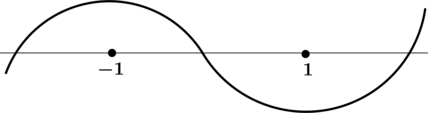
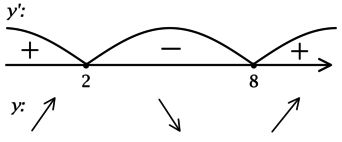
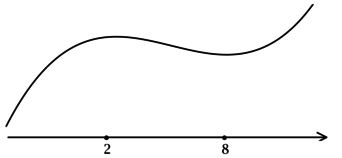
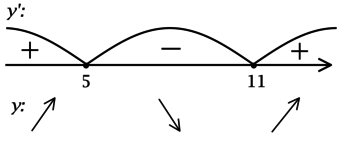
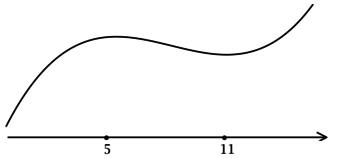
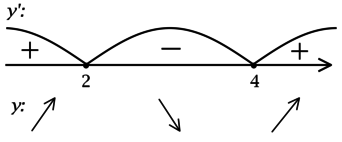
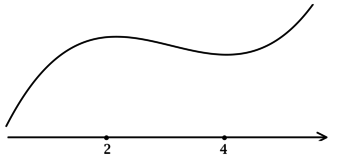
Задачи, при выполнении которых требуется найти точки экстремума у элементарных функций, в ЕГЭ по математике включаются каждый год. Уметь справляться с ними должны школьники, сдающие как базовый уровень экзамена, так и профильный. Научившись безошибочно находить максимум и минимум элементарной функции в задачах ЕГЭ, выпускники смогут выполнить задание и получить конкурентные баллы.
Восполнить пробелы в знаниях и лучше усвоить информацию вам поможет образовательный проект «Школково». Чтобы учащимся было легче справляться с задачами ЕГЭ, в которых необходимо найти минимум и максимум элементарной функции, мы предлагаем прежде всего повторить определения и основные правила. Эту информацию мы разместили в разделе «Теоретическая справка». Здесь собран материал, подготовленный нашими специалистами для выпускников средних школ.
Чтобы закрепить усвоенную информацию и научиться справляться с задачами в ЕГЭ, выполните упражнения, в которых требуется найти точки экстремума у элементарных функций. Богатая подборка задач представлена в разделе «Каталог». Задания здесь регулярно обновляются и дополняются. Выполнить упражнения на нахождение точек экстремума у элементарных функций, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.