\(\blacktriangleright\) Простейшие элементарные функции (ПЭФ) и их производные: \[\begin{array}{|r|c|c|}
\hline & \text{Функция } f(x) & \text{Производная } f'(x)\\
\hline
\textbf{1} & c & 0\\&&\\
\textbf{2} & x^a & a\cdot x^{a-1}\\&&\\
\textbf{3} & \ln x & \dfrac1x\\&&\\
\textbf{4} & \log_ax & \dfrac1{x\cdot \ln a}\\&&\\
\textbf{5} & e^x & e^x\\&&\\
\textbf{6} & a^x & a^x\cdot \ln a\\&&\\
\textbf{7} & \sin x & \cos x\\&&\\
\textbf{8} & \cos x & -\sin x\\[1ex]
\hline
\end{array} \quad \quad \quad \quad
\begin{array}{|r|c|c|}
\hline & \text{Функция } f(x) & \text{Производная } f'(x)\\
\hline
\textbf{9} & \mathrm{tg}\, x & \dfrac1{\cos^2 x}\\&&\\
\textbf{10} & \mathrm{ctg}\, x & -\,\dfrac1{\sin^2 x}\\&&\\
\textbf{11} & \arcsin x & \dfrac1{\sqrt{1-x^2}}\\&&\\
\textbf{12} & \arccos x & -\,\dfrac1{\sqrt{1-x^2}}\\&&\\
\textbf{13} & \mathrm{arctg}\, x & \dfrac1{1+x^2}\\&&\\
\textbf{14} & \mathrm{arcctg}\, x & -\,\dfrac1{1+x^2}\\[0.5ex]
\hline
\end{array}\]
\(\blacktriangleright\) Элементарные функции (ЭФ) — любые линейные комбинации простейших элементарных функций (то есть их сумма, разность, умножение на число).
Пример: \(f(x)=4\cos x +\dfrac{x^3}2\)
\(\blacktriangleright\) Основные формулы поиска производной (\(f=f(x), g=g(x)\) – функции):
1. Умножение функции на число: \[(c\cdot f)'=c\cdot f'\]
2. Сумма или разность двух функций: \[(f\pm g)'=f'\pm
g'\]
\(\blacktriangleright\) Хитрости, упрощающие поиск производной:
I. Т.к. \(\sqrt[n]{x^m}=x^{\frac mn}\), то производную этой функции можно искать по формуле (2).
Частный случай: \(\sqrt x =x^{\frac12}\): \[(\sqrt x)'=\dfrac1{2\sqrt x}\]
II. Т.к. \(\dfrac1{x^a}=x^{-a}\), то производную этой функции можно также искать по формуле (2): \[\left(\dfrac1{x^a}\right)'=-\dfrac a{x^{a+1}}\]
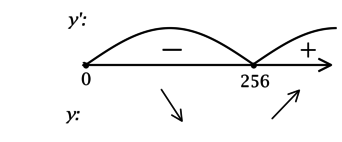
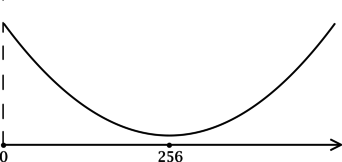
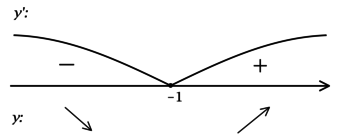
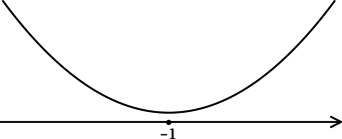
\(\blacktriangleright\) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания (\(f'>0\)) и убывания (\(f'<0\)) функции, критические точки (где \(f'=0\) или \(f'\) не существует).