\(F(x) = x^3 - 2x + 7\) – одна из первообразных функции \(f(x)\). Найдите \(f(0)\).
По определению первообразной \(f(x) = F'(x)\).
Тогда \(f(x) = 3x^2 - 2\), откуда \(f(0) = -2\).
Ответ: -2
7. Взаимосвязь функции и ее производной
\(F(x)\) – первообразная для \(f(x)\), если \(F'(x)=f(x)\) для всех \(x\) из области определения \(f(x)\).
Имеют место следующие формулы:
\(\blacktriangleright F(x)+c = \int f(x)dx,\) \(c\) — число.
\(\blacktriangleright \int_{a}^{b}f(x)dx=F(b)-F(a)\) — формула Ньютона-Лейбница.
\(\blacktriangleright \int_{a}^{b}f(x)dx=S_{\text{кр.тр.}}\) — площадь криволинейной трапеции.
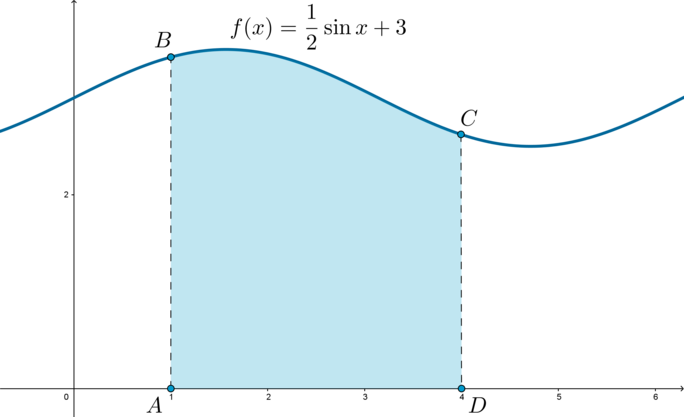
\[{\large{S_{ABCD}=\int_{1}^{4}\left(\dfrac{1}{2}\sin x+3\right)dx}}\]
\(F(x) = x^3 - 2x + 7\) – одна из первообразных функции \(f(x)\). Найдите \(f(0)\).
По определению первообразной \(f(x) = F'(x)\).
Тогда \(f(x) = 3x^2 - 2\), откуда \(f(0) = -2\).
Ответ: -2
\(F(x) = 2x^4 - x^3 + 7x - \pi\) – одна из первообразных функции \(f(x)\). Найдите \(f(1)\).
По определению первообразной \(f(x) = F'(x)\).
Тогда \(f(x) = 8x^3 - 3x^2 + 7\), откуда \(f(1) = 12\).
Ответ: 12
\(F(x) = x^5 - x^4 + x^3 - x^2 + x - 2016\) – одна из первообразных функции \(f(x)\). Найдите \(f(-1)\).
По определению первообразной \(f(x) = F'(x)\).
Тогда \(f(x) = 5x^4 - 4x^3 + 3x^2 - 2x + 1\), откуда \(f(-1) = 15\).
Ответ: 15
На рисунке изображён график функции \(y = f(x)\). Вычислите по рисунку \(F(3) - F(-1)\), где \(F(x)\) – одна из первообразных функции \(y = f(x)\).
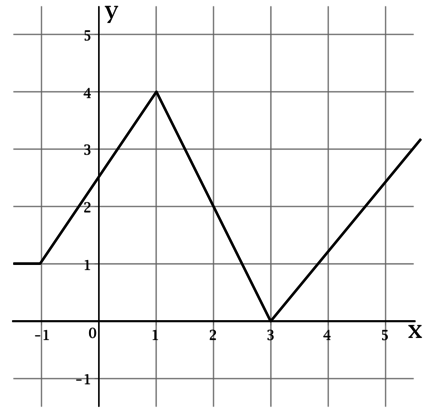
Площадь под графиком неотрицательной функции \(f(x)\) от точки \(x = a\) до точки \(x = b\) равна \(F(b) - F(a)\), где \(F(x)\) – одна из первообразных функции \(y = f(x)\).
Таким образом, \(F(3) - F(-1)\) – площадь под графиком \(y = f(x)\) от точки \(x = -1\) до точки \(x = 3\).
Площадь под графиком \(y = f(x)\) от точки \(x = -1\) до точки \(x = 3\) равна \(9\), тогда \(F(3) - F(-1) = 9\).
Ответ: 9
На рисунке изображён график функции \(y = f(x)\). Вычислите по рисунку \(F(0) - F(2)\), где \(F(x)\) – одна из первообразных функции \(y = f(x)\).
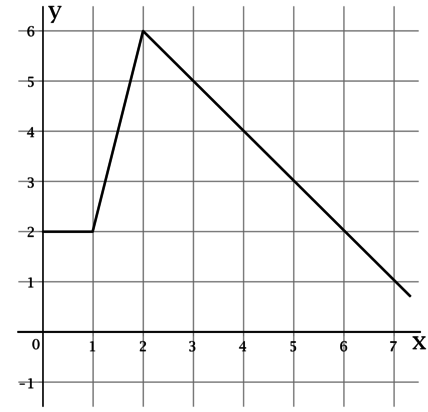
Площадь под графиком неотрицательной функции \(f(x)\) от точки \(x = a\) до точки \(x = b\) равна \(F(b) - F(a)\), где \(F(x)\) – одна из первообразных функции \(y = f(x)\).
Таким образом, \(F(0) - F(2) = -(F(2) - F(0))\) – взятая с минусом площадь под графиком \(y = f(x)\) от точки \(x = 0\) до точки \(x = 2\).
Площадь под графиком \(y = f(x)\) от точки \(x = 0\) до точки \(x = 2\) равна \(6\), тогда \(F(0) - F(2) = -6\).
Ответ: -6
На рисунке изображён график функции \(y = F(x)\) – одной из первообразных некоторой функции \(y = f(x)\), определённой на интервале \((0,2; 8,8)\). Определите по рисунку количество решений уравнения \(f(x) = 0\) на отрезке \([1,5; 7,5]\).
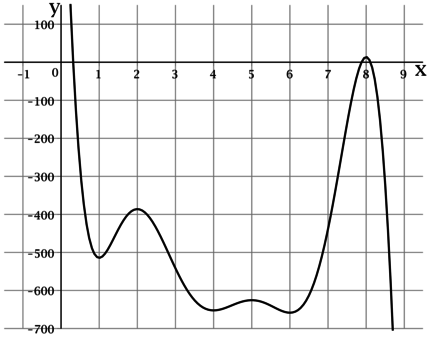
По определению первообразной \(f(x) = F'(x)\), тогда уравнение \(f(x) = 0\) равносильно \(F'(x) = 0\). Производная функции равна \(0\) в точности в тех точках, где касательная к её графику параллельна оси \(Ox\).
По рисунку видно, что на отрезке \([1,5; 7,5]\) касательная к графику \(y = F(x)\) параллельна оси \(Ox\) в \(4\) точках (в точках с абсциссами \(x = 2\), \(x = 4\), \(x = 5\), \(x = 6\)).
Ответ: 4
На рисунке изображён график функции \(y = F(x)\) – одной из первообразных некоторой функции \(y = f(x)\), определённой на интервале \((0,5; 8,5)\). Определите по рисунку количество решений уравнения \(f(x) = 0\) на отрезке \([2,5; 5,5]\).
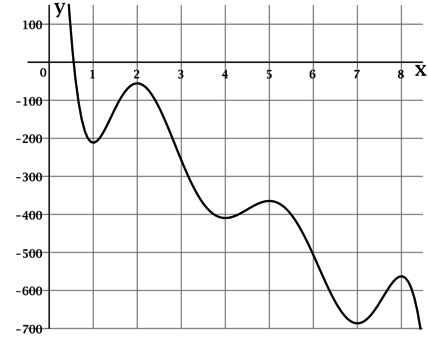
По определению первообразной \(f(x) = F'(x)\), тогда уравнение \(f(x) = 0\) равносильно \(F'(x) = 0\). Производная функции равна \(0\) в точности в тех точках, где касательная к её графику параллельна оси \(Ox\).
По рисунку видно, что на отрезке \([2,5; 5,5]\) касательная к графику \(y = F(x)\) параллельна оси \(Ox\) в \(2\) точках (в точках с абсциссами \(x = 4\), \(x = 5\)).
Ответ: 2
Тот факт, что задания ЕГЭ по теме «Функция как производная своей первообразной» вызывают у выпускников значительные сложности, подтвержден многолетней практикой. В связи с этим еще раз вспомнить базовые алгоритмы выполнения таких задач при подготовке к сдаче экзаменационного испытания просто необходимо.
Занимаясь вместе с математическим порталом «Школково», вы сможете сделать это качественно и эффективно. Чтобы задачи ЕГЭ на нахождение производной и первообразной показательной функции давались старшеклассникам без затруднений, вначале им непременно стоит освежить в памяти базовый теоретический материал. Причем для этого вовсе не обязательно искать нужный параграф в школьном учебнике. Необходимая информация по теме «Производная и первообразная логарифмической функции» уже есть в разделе «Теоретическая справка». Ее специалисты образовательного портала «Школково» подготовили и представили в максимально понятной форме.
Приобрести навык решения задач по теме «Производная и первообразная показательной и логарифмической функции» выпускники также смогут на нашем сайте. Чтобы найти соответствующие упражнения, достаточно перейти в раздел «Каталог». База заданий регулярно дополняется.
Каждое упражнение на сайте содержит алгоритм решения и правильный ответ, например, «Упражения на связь производной со скоростью и ускорением тела». Практиковаться в выполнении задач учащиеся старших классов могут в онлайн-режиме, находясь в столице или другом городе РФ.
Для того чтобы при необходимости быстро найти определенное упражнение, вы можете сохранить его в разделе «Избранное».
© 2024 Все права защищены | Карта сайта
Политика конфиденциальности
Пользовательское соглашение
