\(\blacktriangleright\) Функция \(f(x)\) называется возрастающей на промежутке \(X\), если для любых \(x_1, x_2\in
X\), таких что \(x_1<x_2\), выполнено \(f(x_1)<f(x_2)\).
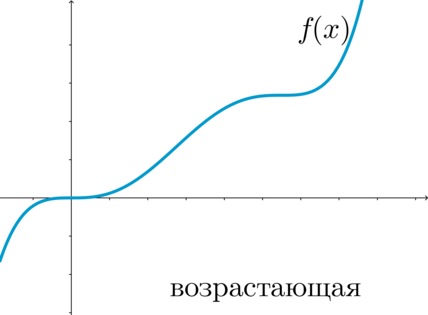
Функция называется неубывающей на промежутке \(X\), если для любых \(x_1, x_2\in X\), таких что \(x_1<x_2\), выполнено \(f(x_1)\leq f(x_2)\).
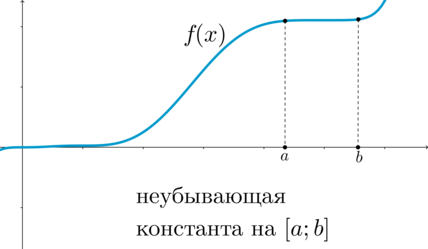
\(\blacktriangleright\) Функция \(f(x)\) называется убывающей на промежутке \(X\), если для любых \(x_1, x_2\in X\), таких что \(x_1<x_2\), выполнено \(f(x_1)>f(x_2)\).
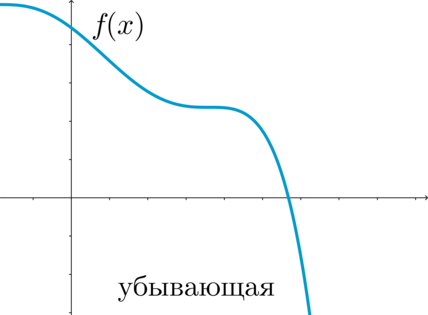
Функция называется невозрастающей на промежутке \(X\), если для любых \(x_1, x_2\in X\), таких что \(x_1<x_2\), выполнено \(f(x_1)\geq f(x_2)\).

\(\blacktriangleright\) Возрастающие и убывающие функции называют строго монотонными, а невозрастающие и неубывающие — просто монотонными.
\(\blacktriangleright\) Основные свойства:
I. Если функция \(f(x)\) — строго монотонна на \(X\), то из равенства \(x_1=x_2\) (\(x_1,x_2\in X\)) следует \(f(x_1)=f(x_2)\), и наоборот.
Пример: функция \(f(x)=\sqrt x\) является строго возрастающей при всех \(x\in [0;+\infty)\), поэтому из равенства \(\sqrt x=\sqrt 4\) следует \(x=4\).
II. Если функция \(f(x)\) — строго монотонна на \(X\), то уравнение \(f(x)=c\), где \(c\) — некоторое число, всегда имеет не более одного решения на \(X\).
Пример: функция \(f(x)=x^2\) является строго убывающей при всех \(x\in
(-\infty;0]\), поэтому уравнение \(x^2=9\) имеет на этом промежутке не более одного решения, а точнее одно: \(x=-3\).
функция \(f(x)=-\dfrac 1{x+1}\) является строго возрастающей при всех \(x\in (-1;+\infty)\), поэтому уравнение \(-\dfrac 1{x+1}=0\) имеет на этом промежутке не более одного решения, а точнее ни одного, т.к. числитель левой части никогда не может быть равен нулю.
III. Если функция \(f(x)\) — неубывает (невозрастает) и непрерывна на отрезке \([a;b]\), причем на концах отрезка она принимает значения \(f(a)=A, f(b)=B\), то при \(C\in [A;B]\) (\(C\in
[B;A]\)) уравнение \(f(x)=C\) всегда имеет хотя бы одно решение.
Пример: функция \(f(x)=x^3\) является строго возрастающей (то есть строго монотонной) и непрерывной при всех \(x\in\mathbb{R}\), поэтому при любом \(C\in (-\infty;+\infty)\) уравнение \(x^3=C\) имеет ровно одно решение: \(x=\sqrt[3]{C}\).