Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1,
\ 2, \ 3, \ 4 \ \) и т.д.
\(\bullet\) Множество целых чисел \(\mathbb{Z}\) состоит из натуральных чисел, противоположных им (\(-1, \ -2, \ -3 \) и т.д.) и нуля \(0\).
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\) (обыкновенные дроби).
Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).
Это просто термины, которые стоит запомнить, чтобы правильно понимать условия задач.
Факт 2.
Таблица умножения: 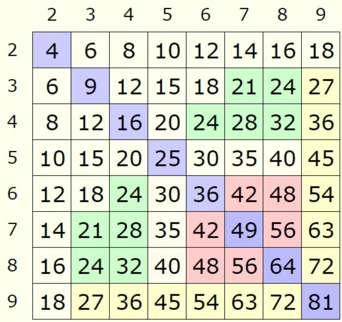
Заметим, что любое целое число можно представить в виде дроби. Например, \(3=\dfrac31\).
Также напоминаем, что при умножении на любое число (не равное нулю) числителя и знаменателя дроби значение этой дроби не меняется. Например, \(\dfrac31=\dfrac62=\dfrac93\) и т.п.
Факт 3.
\(\bullet\) Простое число – это натуральное число, имеющее ровно два делителя: \(1\) и само это число.
Пример: \(2, 3, 5, 7, 11, 13, 17\) и т.д.
Заметим, что число \(1\) не является простым, так как делится только на \(1\), то есть имеет ровно один делитель.
\(\bullet\) Признак делимости на \(2\): число \(a\) делится на \(2\), если оно заканчивается на \(0,2,4,6\) и \(8\). Например, числа \(56\) и \( 900\) делятся на \(2\), а числа \(71\) и \( 1973\) не делятся на \(2\). Числа, делящиеся на \(2\), называются четными; числа, не делящиеся на \(2\), называют нечетными.
Признак делимости на \(3\): число \(a\) делится на \(3\), если его сумма цифр делится на \(3\). Например, числа \(198\) и \( 105\) делятся на \(3\), а числа \(179\) и \( 5869\) не делятся на \(3\).
Признак делимости на \(5\): число \(a\) делится на \(5\), если оно заканчивается на \(5\) или на \(0\). Например, числа \(505\) и \( 160\) делятся на \(5\), а число \(367\) не делится на \(5\).
Признак делимости на \(9\): число \(a\) делится на \(9\), если его сумма цифр делится на \(9\). Например, числа \(198\) и \( 108\) делятся на \(9\), а числа \(149\) и \( 5109\) не делятся на \(9\).
Признак делимости на \(10\): число \(a\) делится на \(10\), если оно заканчивается на \(0\). Например, числа \(50\) и \( 160\) делятся на \(10\), а число \(367\) не делится на \(10\).
\(\bullet\) Разложение числа на простые множители – это запись этого числа в виде произведения простых чисел.
Пример: \(4200=2^3\cdot 3\cdot 5^2\cdot 7\).
Как разложить число на простые множители? Покажем на примере. Пусть нужно разложить число \(4200\) на простые множители. Видим, что число \(4200\) делится на \(100\), причем \(4200:100=42\). Следовательно, \(4200=100\cdot 42\). Так как \(100=10\cdot 10=2\cdot 5\cdot 2\cdot
5=2^2\cdot 5^2\), а \(42=6\cdot 7=2\cdot 3\cdot 7\), то получаем: \[4200=2^2\cdot 5^2\cdot 2\cdot 3\cdot 7=2^3\cdot 5^2\cdot 3\cdot 7\] Разложение на простые множители используется при сокращении дробей.
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
\(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot
2\llap{/}}{3\cdot
2\llap{/}}=\dfrac{49}3\\[2ex]
&\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot
7\llap{/}}{7\llap{/}\cdot
5}=\dfrac 85\\[2ex]
&\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot
3\cdot
2\llap{/}}=\dfrac{14}{15}\end{aligned}\)
Заметим, что если ответом к задаче является дробь, то она должна быть несократимой, то есть ее числитель и знаменатель не должны иметь общих делителей. Например, будет неправильным записать ответ к задаче как \(\dfrac{13}{65}\). Нужно заметить, что \(65=13\cdot
5\), следовательно, \[\dfrac{13}{65}=\dfrac{13\llap{/}}{5\cdot 13\llap{/}}=\dfrac15\] То есть правильным ответом будет \(\dfrac15\).
Факт 4.
\(\bullet\) Правила сложения дробей: Значит, когда мы складываем две дроби с одинаковыми знаменателями, мы получаем дробь, у которой :
– знаменатель остается таким же;
– числитель равен сумме числителей этих двух дробей.
Точно так же мы поступаем и с разностью двух дробей. Значит, когда мы складываем две дроби с разными знаменателями, мы:
– приводим их к одинаковому знаменателю, домножив первую дробь на знаменатель второй, а вторую – на знаменатель первой;
– таким образом мы получаем две дроби с одинаковыми знаменателями и их можно сложить как дроби с одинаковыми знаменателями (то есть пользуясь первой формулой).
Это первый, более сложный способ сложения двух дробей с разными знаменателями. Второй способ, который упрощает вычисления и тем самым уменьшает вероятность допустить вычислительную ошибку, будет показан чуть позже
Примеры:
1) \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)
2) \(\dfrac{17}2-\dfrac{11}2=\dfrac{17-11}2=\dfrac62\)
3) \(\dfrac12+\dfrac{11}3=\dfrac{1\cdot 3+11\cdot 2}{2\cdot
3}=\dfrac{25}{6}\)
\(\bullet\) Правила умножения дробей: Если мы умножаем две дроби, то мы получаем дробь, у которой:
– числитель равен произведению числителей двух дробей;
– знаменатель равен произведению знаменателей двух дробей.
Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)
\(\bullet\) Правила деления дробей: Данное правило часто называют так: <<чтобы разделить одну дробь на вторую, нужно первую дробь умножить на “перевернутую” вторую>>.
Пример:
1) \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\);
2) \(\dfrac 12:3=\dfrac12:\dfrac31=\dfrac12\cdot \dfrac13=\dfrac16\)
\(\bullet\) Для того, чтобы перевести дробь смешанную дробь, например, \(4\dfrac{5}{11}\), в неправильную, нужно проделать следующие действия: \[4+\dfrac5{11}=\dfrac41+\dfrac5{11}=\dfrac{4\cdot
11+5}{11}=\dfrac{49}{11}\]
\(\bullet\) Разложение чисел на простые множители, помимо сокращения дробей, необходимо для того, чтобы наиболее оптимально приводить дроби к общему знаменателю (общий знаменатель – число, которое делится на знаменатель каждой дроби).
Пусть нам нужно привести две дроби \(\dfrac1{21}\) и \(\dfrac1{15}\) к общему знаменателю. По правилу из Факта 3 можно просто перемножить их знаменатели и получить дроби \(\dfrac{15}{21\cdot 15}\) и \(\dfrac{21}{15\cdot 21}\).
Но тогда общий знаменатель этих дробей получается достаточно большим: \(15\cdot 21=315\).
Покажем другой оптимальный способ приведения дробей к общему знаменателю. Так как \(21=7\cdot 3\) и \(15=3\cdot 5\), то наименьшее число, которое делится и на \(21\), и на \(15\) – это \(7\cdot 3\cdot
5=105\). Следовательно, это и есть их наименьший общий знаменатель. Для того, чтобы дробь \(\dfrac1{21}\) имела знаменатель \(105\), нужно умножить ее числитель и знаменатель на \(5\); для того, чтобы дробь \(\dfrac1{15}\) имела знаменатель \(105\), нужно умножить ее числитель и знаменатель на \(7\). Таким образом, получаем: \(\dfrac1{21}=\dfrac5{105}\) и \(\dfrac1{15}=\dfrac7{105}\).
Покажем еще один пример, демонстрирующий, что не всегда удобно и нужно раскладывать знаменатели прямо до простых множителей. Пусть нам нужно сложить дроби \(\dfrac1{49}\) и \(\dfrac1{98}\). Замечаем,что \(98=2\cdot 49\) (для того, чтобы это заметить, нужно хорошо выучить таблицу умножения и потренировать устный счет ). Тогда можно записать \(\dfrac1{49}\) и \(\dfrac1{2\cdot 49}\). Следовательно, для того, чтобы у дробей стали одинаковые знаменатели, нужно всего лишь домножить первую дробь на \(2\): \(\dfrac2{2\cdot 49}\) и \(\dfrac1{2\cdot 49}\).
А теперь представьте, что вы пользуетесь первым способом. Тогда ваш общий знаменатель будет равен \(49\cdot 98=4802\)! Неудобно, верно?




