Задача 1
Решите уравнение \[\sin x=-a, \quad 0<a<1\]
Решение
\(\arcsin(-a)\) – это такой угол из отрезка \(\left[-\dfrac{\pi}2;
\dfrac{\pi}2\right]\), синус которого равен \(-a\): 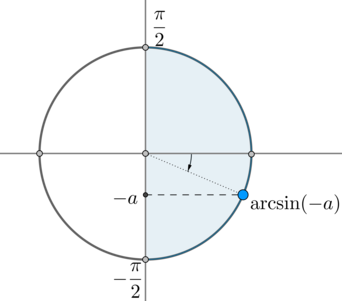
Следовательно, одна серия решений данного уравнения – это \(x=\arcsin(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, синус в которой равен \(-a\) – угол \(\alpha\): 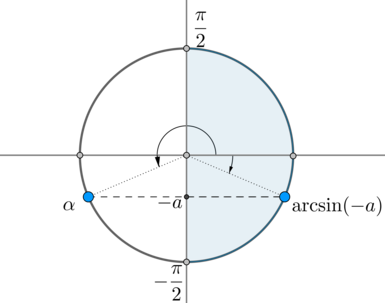
Заметим, что \(\alpha=\pi+(-\arcsin(-a))\). Так как \(\arcsin(-a)=-\arcsin a\), то \(\alpha=\pi+\arcsin a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=-\arcsin a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=\pi+\arcsin a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\]
Задача 2
Решите уравнение \[\cos x=-a, \quad 0<a<1\]
Решение
\(\arccos(-a)\) – это такой угол из отрезка \(\left[0; \pi\right]\), косинус которого равен \(-a\): 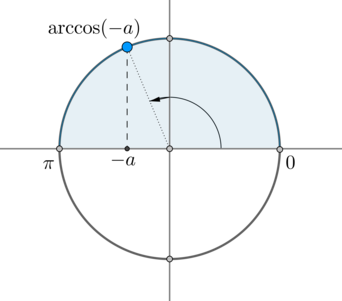
Следовательно, одна серия решений данного уравнения – это \(x=\arccos(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, косинус в которой равен \(-a\) – угол \(\alpha\): 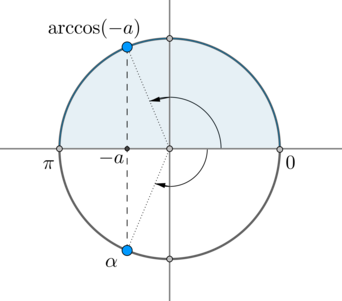
Заметим, что \(\alpha=-\arccos(-a)\). Так как \(\arccos(-a)=\pi-\arccos
a\), то \(\alpha=-\pi+\arccos a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=\pi-\arccos
a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=-\pi+\arccos a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\]
Задача 3
Решите уравнение \[\mathrm{tg}\, x=-a, a>0\]
Решение
\(\mathrm{arctg}\,(-a)\) – это такой угол из промежутка \(\left(-\dfrac{\pi}2;\dfrac{\pi}2\right)\), тангенс которого равен \(-a\): 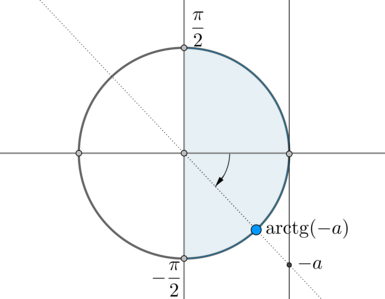
Следовательно, одна серия решений данного уравнения – это \(x=\mathrm{arctg}\,(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, тангенс в которой равен \(-a\) – угол \(\alpha\): 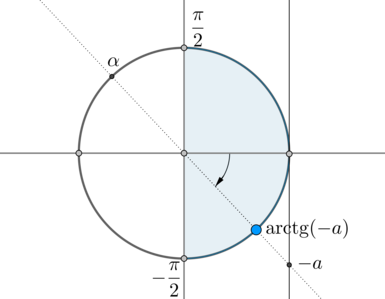
Заметим, что \(\alpha=\mathrm{arctg}\,(-a)+\pi\). Так как \(\mathrm{arctg}\,(-a)=-\mathrm{arctg}\, a\), то \(\alpha=\pi-\mathrm{arctg}\, a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=-\mathrm{arctg}\, a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=\pi-\mathrm{arctg}\, a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\] Заметим, что так как углы \(-\mathrm{arctg}\, a\) и \(\pi-\mathrm{arctg}\, a\) отличаются друг от друга на \(\pi\), то ответ можно записать в виде одной серии корней с периодом \(\pi\): \[x=-\mathrm{arctg}\, a+\pi m, m\in\mathbb{Z}\]
Задача 4
Решите уравнение \[\mathrm{ctg}\, x=-a, a>0\]
Решение
\(\mathrm{arcctg}\,(-a)\) – это такой угол из промежутка \(\left(0;\pi\right)\), котангенс которого равен \(-a\): 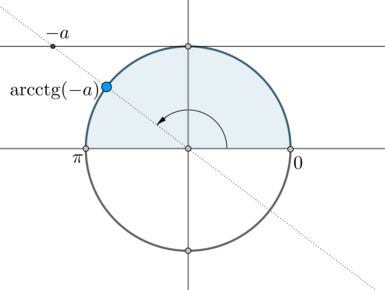
Следовательно, одна серия решений данного уравнения – это \(x=\mathrm{arcctg}\,(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, котангенс в которой равен \(-a\) – угол \(\alpha\): 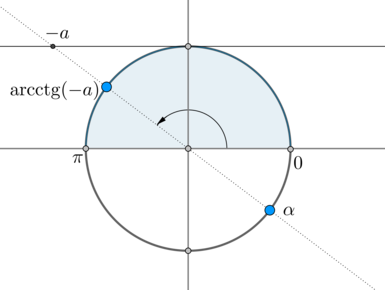
Заметим, что \(\alpha=\mathrm{arcctg}\,(-a)+\pi\). Так как \(\mathrm{arcctg}\,(-a)=\pi-\mathrm{arcctg}\, a\), то \(\alpha=2\pi-\mathrm{arcctg}\, a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=\pi-\mathrm{arcctg}\, a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=2\pi-\mathrm{arcctg}\, a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\] Заметим, что так как углы \(2\pi-\mathrm{arcctg}\, a\) и \(\pi-\mathrm{arcctg}\, a\) отличаются друг от друга на \(\pi\), то ответ можно записать в виде одной серии корней с периодом \(\pi\): \[x=\pi-\mathrm{arcctg}\, a+\pi m, m\in\mathbb{Z}\]











