\({\color{red}{\textbf{Факт 1. Про параллельность прямых}}}\)
\(\bullet\) Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
\(\bullet\) Через две параллельные прямые проходит плоскость, и притом только одна.
\(\bullet\) Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
\(\bullet\) Если прямая \(a\) параллельна прямой \(b\), а та в свою очередь параллельна прямой \(c\), то \(a\parallel c\).
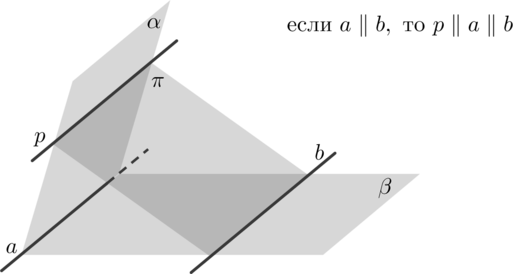
\(\bullet\) Пусть плоскость \(\alpha\) и \(\beta\) пересекаются по прямой \(a\), плоскости \(\beta\) и \(\pi\) пересекаются по прямой \(b\), плоскости \(\pi\) и \(\alpha\) пересекаются по прямой \(p\). Тогда если \(a\parallel
b\), то \(p\parallel a\) (или \(p\parallel b\)):
\({\color{red}{\textbf{Факт 2. Про параллельность прямой и плоскости}}}\)
\(\bullet\) Существует три вида взаимного расположения прямой и плоскости:
1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости);
2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость);
3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).
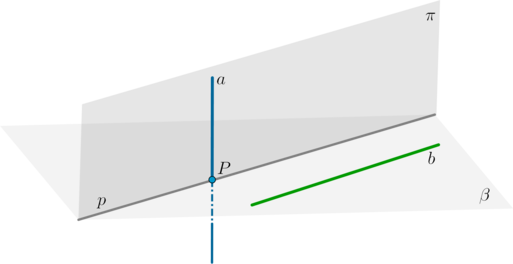
\(\bullet\) Если прямая \(a\), не лежащая в плоскости \(\pi\), параллельна некоторой прямой \(p\), лежащей в плоскости \(\pi\), то она параллельна данной плоскости.

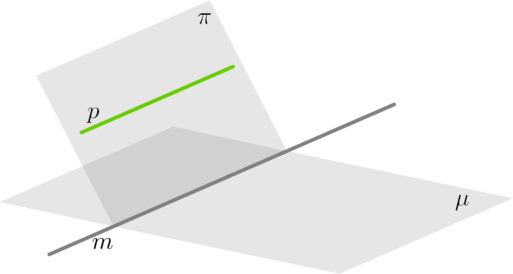
\(\bullet\) Пусть прямая \(p\) параллельна плоскости \(\mu\). Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\), то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\).
\({\color{red}{\textbf{Факт 3. Про параллельность плоскостей}}}\)
\(\bullet\) Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.
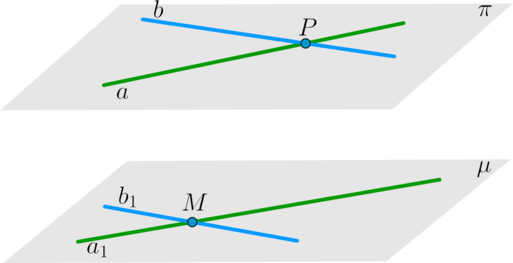
\(\bullet\) Если две пересекающиеся прямые из одной плоскости соответственно параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
\(\bullet\) Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны: \[\alpha\parallel \beta, \ \alpha\cap \gamma=a,
\ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

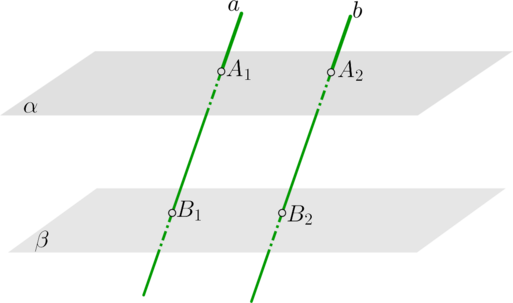
\(\bullet\) Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны: \[\alpha\parallel \beta, \ a\parallel b \Longrightarrow
A_1B_1=A_2B_2\]
\({\color{red}{\textbf{Факт 4. Про скрещивающиеся прямые}}}\)
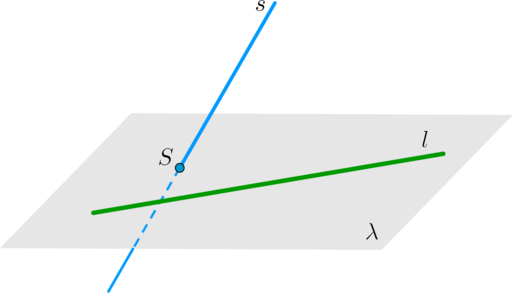
\(\bullet\) Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
\(\bullet\) Признак:
Пусть прямая \(l\) лежит в плоскости \(\lambda\). Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\), не лежащей на прямой \(l\), то прямые \(l\) и \(s\) скрещиваются.
\(\bullet\) алгоритм нахождения угла между скрещивающимися прямыми \(a\) и \(b\):
Шаг 1. Через одну из двух скрещивающихся прямых \(a\) провести плоскость \(\pi\) параллельно другой прямой \(b\). Как это сделать: проведем плоскость \(\beta\) через прямую \(b\) так, чтобы она пересекала прямую \(a\) в точке \(P\); через точку \(P\) проведем прямую \(p\parallel b\); тогда плоскость, проходящая через \(a\) и \(p\), и есть плоскость \(\pi\).
Шаг 2. В плоскости \(\pi\) найти угол между прямыми \(a\) и \(p\) (\(p\parallel b\)). Угол между ними будет равен углу между скрещивающимися прямыми \(a\) и \(b\).
\({\color{red}{\textbf{Факт 5. Про перпендикулярность прямой и плоскости}}}\)
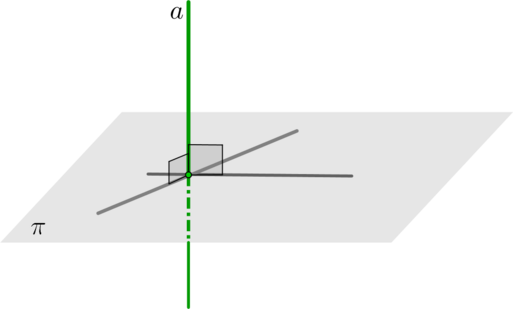
\(\bullet\) Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
\(\bullet\) Если две прямые перпендикулярны плоскости, то они параллельны.
\(\bullet\) Признак: если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
\({\color{red}{\textbf{Факт 6. Про расстояния}}}\)
\(\bullet\) Для того, чтобы найти расстояние между параллельными прямыми, нужно из любой точки одной прямой опустить перпендикуляр на другую прямую. Длина перпендикуляра и есть расстояние между этими прямыми.
\(\bullet\) Для того, чтобы найти расстояние между плоскостью и параллельной ей прямой, нужно из любой точки прямой опустить перпендикуляр на эту плоскость. Длина перпендикуляра и есть расстояние между этими прямой и плоскостью.
\(\bullet\) Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.
\(\bullet\) алгоритм нахождения расстояния между скрещивающимися прямыми \(a\) и \(b\):
Шаг 1. Через одну из двух скрещивающихся прямых \(a\) провести плоскость \(\pi\) параллельно другой прямой \(b\). Как это сделать: проведем плоскость \(\beta\) через прямую \(b\) так, чтобы она пересекала прямую \(a\) в точке \(P\); через точку \(P\) проведем прямую \(p\parallel b\); тогда плоскость, проходящая через \(a\) и \(p\), и есть плоскость \(\pi\).
Шаг 2. Найдите расстояние от любой точки прямой \(b\) до плоскости \(\pi\). Это расстояние и есть расстояние между скрещивающимися прямыми \(a\) и \(b\).
\({\color{red}{\textbf{Факт 7. Про теорему о трех перпендикулярах (ТТП)}}}\)
\(\bullet\) Пусть \(AH\) – перпендикуляр к плоскости \(\beta\). Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\). Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции: \[\begin{aligned}
&1. AH\perp \beta, \ AB\perp x\quad \Rightarrow\quad BH\perp x\\[2ex]
&2. AH\perp \beta, \ BH\perp x\quad\Rightarrow\quad AB\perp
x\end{aligned}\] 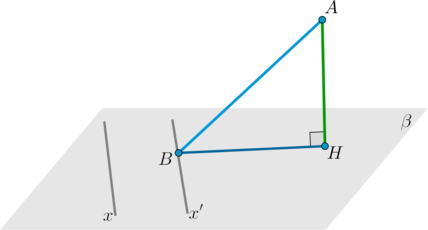
Заметим, что прямая \(x\) необязательно должна проходить через точку \(B\). Если она не проходит через точку \(B\), то строится прямая \(x'\), проходящая через точку \(B\) и параллельная \(x\). Если, например, \(x'\perp BH\), то и \(x\perp BH\).
\({\color{red}{\textbf{Факт 8. Про угол между прямой и плоскостью,
а также угол между плоскостями}}}\)
\(\bullet\) Угол между наклонной прямой и плоскостью — это угол между этой прямой и ее проекцией на данную плоскость. Таким образом, данный угол принимает значения из промежутка \((0^\circ;90^\circ)\).
Если прямая лежит в плоскости, то угол между ними считается равным \(0^\circ\). Если прямая перпендикулярна плоскости, то, исходя из определения, угол между ними равен \(90^\circ\).
\(\bullet\) Чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку \(A\) на этой прямой и провести перпендикуляр \(AH\) к плоскости. Если \(B\) – точка пересечения прямой с плоскостью, то \(\angle ABH\) и есть искомый угол.
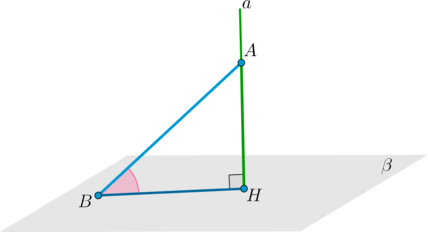
\(\bullet\) Для того, чтобы найти угол между плоскостями \(\alpha\) и \(\beta\), можно действовать по следующему алгоритму:
Отметить произвольную точку \(A\) в плоскости \(\alpha\).
Провести \(AH\perp h\), где \(h\) — линия пересечения плоскостей.
Провести \(AB\) перпендикулярно плоскости \(\beta\).
Тогда \(AB\) – перпендикуляр к плоскости \(\beta\), \(AH\) – наклонная, следовательно, \(HB\) – проекция. Тогда по ТТП \(HB\perp h\).
Следовательно, \(\angle AHB\) — линейный угол двугранного угла между плоскостями. Градусная мера этого угла и есть градусная мера угла между плоскостями.
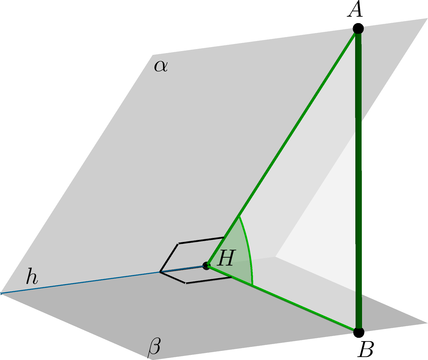
Заметим, что мы получили прямоугольный треугольник \(\triangle AHB\) (\(\angle B=90^\circ\)). Как правило, находить \(\angle AHB\) удобно из него.
\({\color{red}{\textbf{Факт 9. Про перпендикулярность плоскостей}}}\)
\(\bullet\) Признак: если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости. \[a\perp \beta, \ a\in \alpha\quad\Rightarrow\quad \alpha\perp \beta\] 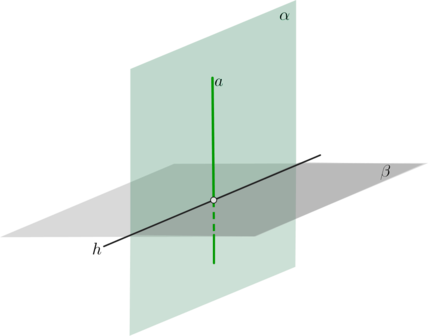
\(\bullet\) Заметим, что так как через прямую \(a\) можно провести бесконечное множество плоскостей, то существует бесконечное множество плоскостей, перпендикулярных \(\beta\) (и проходящих через \(a\)).
















