\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad
\mathrm{tg}\,x=b,\quad
\mathrm{ctg}\,x=b\), которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb{R}\).
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\)).
\[{\color{red}{\text{Решение простейших тригонометрических уравнений}}}\]
Рассмотрим несколько примеров:
Пример 1. Решить уравнение \(\sin x=\dfrac12\).
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\), где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
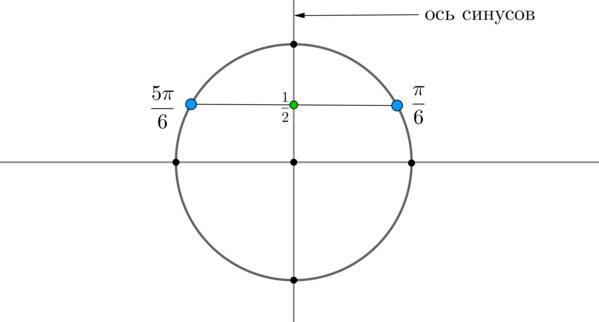
Таким образом, решением являются \(x_1=\dfrac{\pi}6+2\pi n,\
x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}\).
Пример 2. Решить уравнение \(\cos x=-\dfrac{\sqrt2}{2}\).
Найдем на оси косинусов точку \(-\dfrac{\sqrt2}{2}\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac{\sqrt2}{2}\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{3\pi}4\) и \(-\dfrac{3\pi}4\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число.
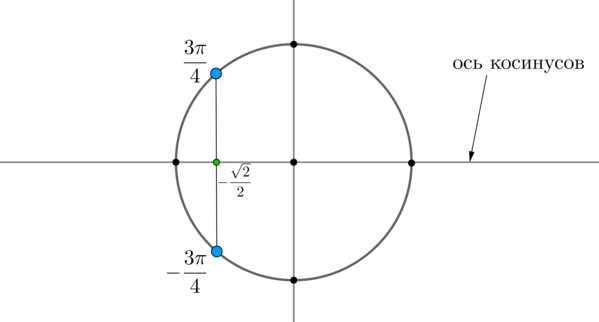
Таким образом, решением являются \(x_1=\dfrac{3\pi}4+2\pi n,\
x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\,x=\dfrac{\sqrt3}3\).
Найдем на оси тангенсов точку \(\dfrac{\sqrt3}3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac{\sqrt3}3\).Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi
n\).
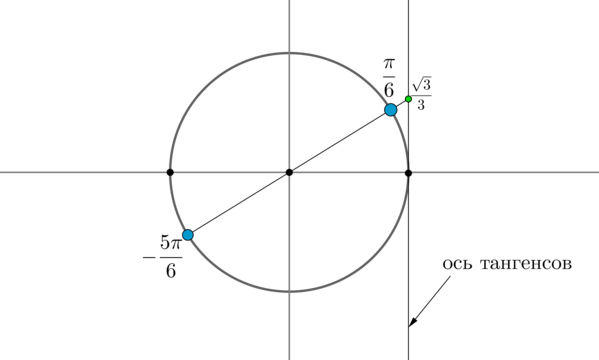
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
Пример 4. Решить уравнение \(\mathrm{ctg}\,x=\sqrt3\).
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi
n\).
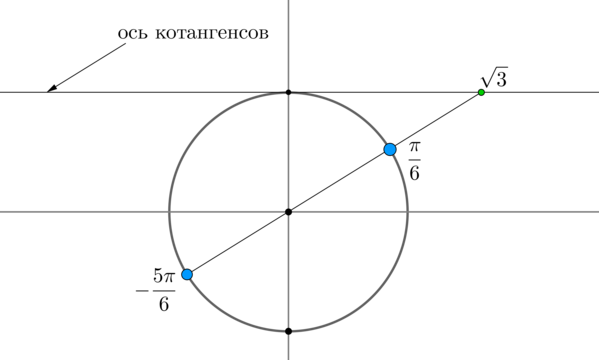
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin{array}{l|c|c}
\hline \text{Уравнение} & \text{Ограничения} & \text{Решение}\\
\hline &&\\
\sin x=a & -1\leq a\leq 1 & \left[
\begin{gathered}
\begin{aligned}
&x=\arcsin a+2\pi n\\
&x=\pi -\arcsin a+2\pi n
\end{aligned}
\end{gathered}
\right. \ \ , \ n\in \mathbb{Z}\\&&\\
\hline &&\\
\cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{tg}\, x=b & b\in \mathbb{R} & x=\mathrm{arctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{ctg}\,x=b & b\in \mathbb{R} & x=\mathrm{arcctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline
\end{array}\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}\).
\(\blacktriangleright\) Любые уравнения вида \(\mathrm{G}\,\big(f(x)\big)=a\), (где \(\mathrm{G}\) — одна из функций \(\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}\), а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\).
Пример 5. Решить уравнение \(\sin{(\pi
x+\dfrac{\pi}3)}=1\).
Сделав замену \(t=\pi x+\dfrac{\pi}3\), мы сведем уравнение к виду \(\sin t=1\). Решением данного уравнения являются \(t=\dfrac{\pi}2+2\pi
n, n\in\mathbb{Z}\).
Теперь сделаем обратную замену и получим: \(\pi
x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n\), откуда \(x=\dfrac16+2n,\
n\in\mathbb{Z}\).
\[{\color{red}{\text{Объединение корней}}}\]
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}\), где \(\alpha\) — один из этих углов.
Рассмотрим данную ситуацию на примере:
Пример 6. Допустим, решением системы являются \(x_1=\pm
\dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \
n\in\mathbb{Z}\). Отметим эти точки на окружности:
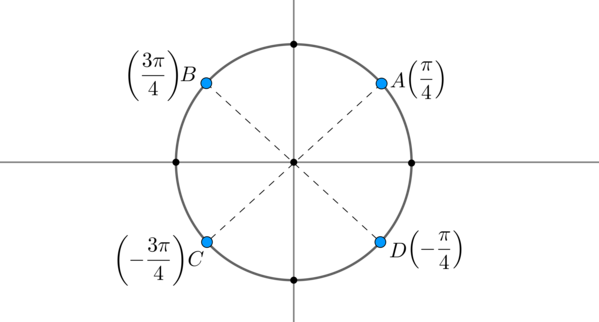
Заметим, что длины дуг \(\buildrel\smile\over{AB},
\buildrel\smile\over{BC}, \buildrel\smile\over{CD},
\buildrel\smile\over{DA}\) равны \(\dfrac{\pi}2\), то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac{\pi}4+\dfrac{\pi}2n, \
n\in\mathbb{Z}\).
\[{\color{red}{\text{Геометрическая интерпретация решений неравенств
вида }\mathrm{G}\,(x) \lor a,}}\]
где \(\lor\) — один из знаков \(\leq,\ <,\ >,\ \geq\).
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x
>\dfrac12\).
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, синус которых больше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
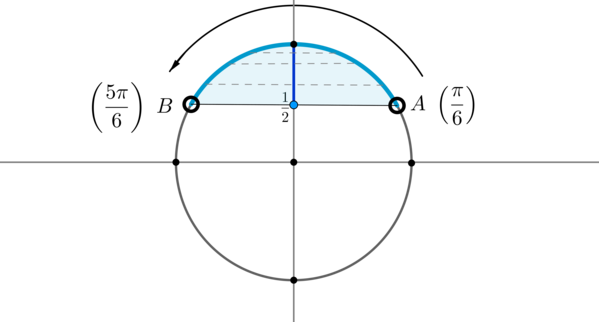
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}6\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}6\), но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}6\). Тогда все числа из промежутка \(\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi
n\right), n\in\mathbb{Z}\), т.к. у синуса период \(2\pi\).
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x
<\dfrac12\).
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, косинус которых меньше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
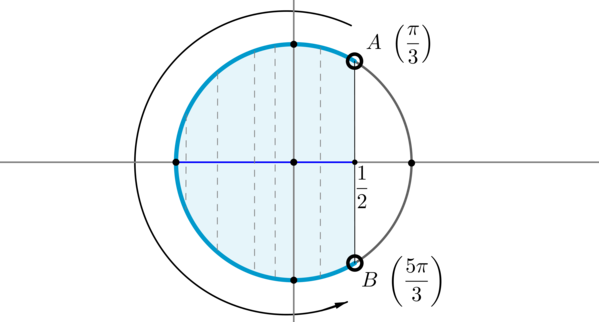
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}3\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}3\), но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}3\). Тогда все числа из промежутка \(\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi
n\right), n\in\mathbb{Z}\), т.к. у косинуса период \(2\pi\).
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm{tg}\, x
\geq \dfrac{\sqrt{3}}3\).
Для начала отметим на окружности корни уравнения \(\mathrm{tg}\, x =
\dfrac{\sqrt{3}}3\). Это точки \(A\) и \(B\). Все точки, тангенс которых больше или равен \(\dfrac{\sqrt{3}}3\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.
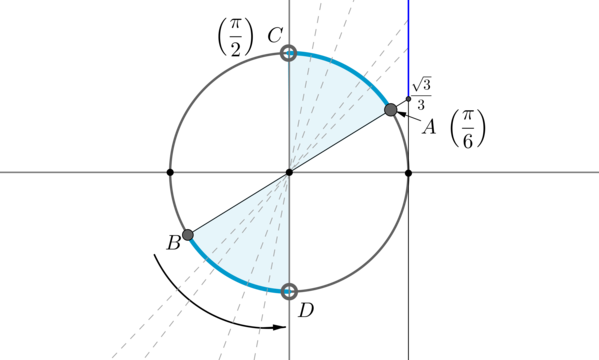
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac{\pi}2\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\dfrac{\pi}2\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\dfrac{\pi}2+\pi n\Big),
n\in\mathbb{Z}\), т.к. у тангенса период \(\pi\).
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm{ctg}\, x
\leq \sqrt{3}\).
Для начала отметим на окружности корни уравнения \(\mathrm{ctg}\, x =
\sqrt{3}\). Это точки \(A\) и \(B\). Все точки, котангенс которых меньше или равен \(\sqrt{3}\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.
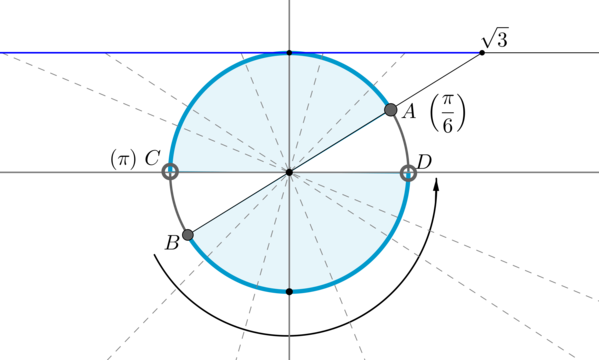
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\pi\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\pi\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\pi+\pi n\Big), n\in\mathbb{Z}\), т.к. период котангенса \(\pi\).
\[{\color{red}{\text{Отбор корней}}}\]
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\), если \(\cos x\ne \dfrac{\sqrt3}2\).
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac{\pi}6+2\pi n,\
x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}\), решением второго являются \(x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}\). Отметим эти точки на окружности:
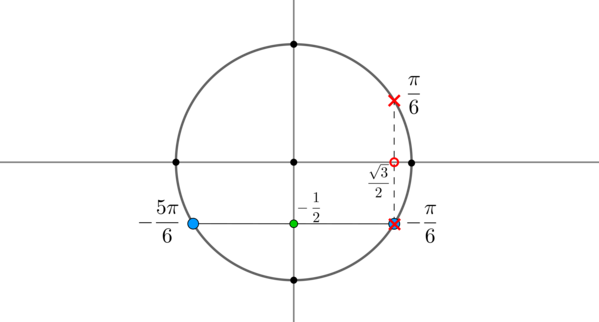
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac{\pi}6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}\).
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin{aligned}
&\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n -
\text{ четном}\\ -\sin \alpha, \text{при } n - \text{ нечетном}
\end{cases}\\
&\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n -
\text{ четном}\\ -\cos \alpha, \text{при } n - \text {нечетном}
\end{cases}\\
&\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\
&\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\
&\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\
&\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\
&\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\
&\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha
\end{aligned}\]
Пример 12. Решить систему \(\begin{cases} \cos x=\dfrac12\\
\sin x+\cos x>0\end{cases}\)
Решением уравнения являются \(x_1=\dfrac{\pi}3+2\pi n,\
x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}\). Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:
\(\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0\), следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0\), следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac{\pi}3+2\pi
n,\ n\in\mathbb{Z}\).
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac{\sqrt2}2\), принадлежащие отрезку \([0;\pi]\).
Решением уравнения являются \(x_1=\dfrac{\pi}4+2\pi n, \
x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}\). Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq
x_2\leq\pi\):
\(0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq
n\leq\dfrac38\). Таким образом, единственное целое значение \(n\), удовлетворяющее этому неравенству, это \(n=0\). При \(n=0\) \(x_1=\dfrac{\pi}4\) — входит в отрезок \([0;\pi]\).
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac{3\pi}4\).
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
\[ax+by=c, \quad a,b,c - \text{целые числа}\]
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\).
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\). Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\), то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\). Т.к. \(НОД(3,5)=1\), то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\):
\[x=\dfrac{2-5y}3=\dfrac{2-2y}3-y\]
Число \(\dfrac{2-2y}3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\): \(0\), \(1\) или \(2\).
Если \(y\) при делении на \(3\) имеет остаток \(0\), то оно записывается как \(y=3p+0\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2\cdot
3p}3=\dfrac23-2p\ne \text{целому числу}\]
Если \(y\) при делении на \(3\) имеет остаток \(1\), то оно записывается как \(y=3p+1\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\), а \(x=\dfrac{2-2y}3-y=-5p-1\).
Ответ: \((-5p-1; 3p+1), p\in\mathbb{Z}\).
Перейдем к примеру:
Пример 14. Решить систему \[\begin{cases}
\sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt]
\cos \dfrac x2=1
\end{cases}\]
Решим первое уравнение системы:
\[\left[ \begin{gathered} \begin{aligned}
&\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt]
&\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered}
\right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[
\begin{gathered} \begin{aligned}
&x=\pi+6\pi n\\
&x=2\pi +6\pi m
\end{aligned} \end{gathered}
\right.\quad n,m\in\mathbb{Z}\]
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}\]
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\), при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\):
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\), то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\), при которых совпадают решения в сериях \(2\pi
+6\pi m\) и \(4\pi k\):
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac{3m+1}2=m+\frac{m+1}2\).
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\).
Если \(m=2p+0\), то \(\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\), то \(\frac{m+1}2=\frac{2p+1+1}2=p+1= \) целому числу.
Значит, \(m=2p+1\), тогда \(k=3p+2\), \(p\in\mathbb{Z}\).
Подставим либо \(m\), либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p,
p\in\mathbb{Z}\).













