Определения
Окружность \(S\) вписана в угол \(\alpha\), если \(S\) касается сторон угла \(\alpha\).
Окружность \(S\) вписана в многоугольник \(P\), если \(S\) касается всех сторон \(P\).
В этом случае многоугольник \(P\) называется описанным около окружности.
Теорема
Центр вписанной в угол окружности лежит на его биссектрисе.
Доказательство
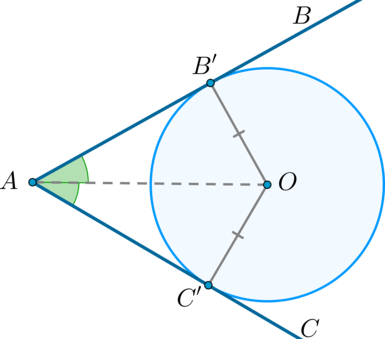
Пусть \(O\) – центр некоторой окружности, вписанной в угол \(BAC\). Пусть \(B'\) – точка касания окружности и \(AB\), а \(C'\) – точка касания окружности и \(AC\), тогда \(OB'\) и \(OC'\) – радиусы, проведённые в точки касания, следовательно, \(OC'\perp AC\), \(OB'\perp
AB\), \(OC' = OB'\).
Значит, треугольники \(AC'O\) и \(AB'O\) – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда \(\angle CAO = \angle BAO\), что и требовалось доказать.
Теорема
В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.
Доказательство
Проведем биссектрисы углов \(\angle A\) и \(\angle B\). Пусть они пересеклись в точке \(O\).
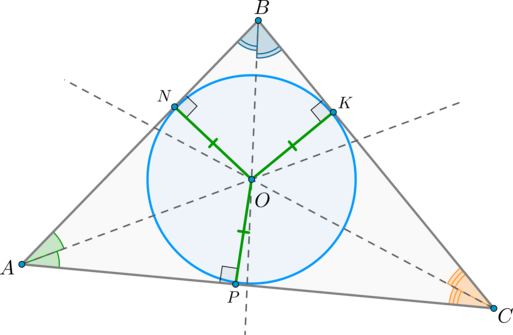
Т.к. \(O\) лежит на биссектрисе \(\angle A\), то расстояния от точки \(O\) до сторон угла равны: \(ON=OP\).
Т.к. \(O\) также лежит на биссектрисе \(\angle B\), то \(ON=OK\). Таким образом, \(OP=OK\), следовательно, точка \(O\) равноудалена от сторон угла \(\angle C\), следовательно, лежит на его биссектрисе, т.е. \(CO\) – биссектриса \(\angle C\).
Таким образом, точки \(N, K, P\) равноудалены от точки \(O\), то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.
Данная окружность единственна, т.к. если предположить, что существует другая вписанная в \(\triangle ABC\) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.
Таким образом, попутно была доказана следующая теорема:
Следствие
Биссектрисы треугольника пересекаются в одной точке.
Теорема о площади описанного треугольника
Если \(a,b,c\) – стороны треугольника, а \(r\) – радиус вписанной в него окружности, то площадь треугольника \[S_{\triangle}=p\cdot r\] где \(p=\dfrac{a+b+c}2\) – полупериметр треугольника.
Доказательство
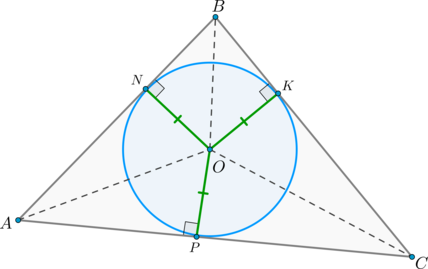
\(S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle AOB}+S_{\triangle
BOC}=\frac12OP\cdot AC+\frac12 ON\cdot AB+\frac12 OK\cdot BC\).
Но \(ON=OK=OP=r\) – радиусы вписанной окружности, следовательно,
\[S_{\triangle ABC}=\frac12 r (AC+AB+BC)=p\cdot r\]
Следствие
Если в многоугольник вписана окружность и \(r\) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на \(r\): \[S_{\text{опис.мног-к}}=p\cdot r\]
Теорема
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство
Необходимость. Докажем, что если в \(ABCD\) вписана окружность, то \(AB+CD=BC+AD\).
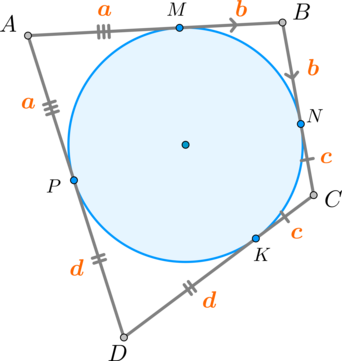
Пусть \(M,N,K,P\) – точки касания окружности и сторон четырехугольника. Тогда \(AM, AP\) – отрезки касательных к окружности, проведенные из одной точки, следовательно, \(AM=AP=a\). Аналогично, \(BM=BN=b, \ CN=CK=c, \ DK=DP=d\).
Тогда: \(AB+CD=a+b+c+d=BC+AD\).
Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Проведем биссектрисы углов \(\angle A\) и \(\angle B\), пусть они пересекутся в точке \(O\). Тогда точка \(O\) равноудалена от сторон этих углов, то есть от \(AB, BC, AD\). Впишем окружность в \(\angle A\) и \(\angle B\) с центром в точке \(O\). Докажем, что эта окружность будет касаться и стороны \(CD\).
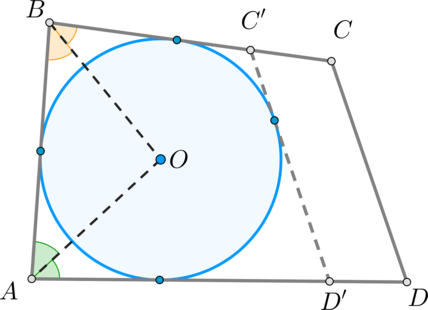
Предположим, что это не так. Тогда \(CD\) либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).
Проведем касательную прямую \(C'D' \parallel CD\) (как показано на рисунке). Тогда \(ABC'D'\) – описанный четырехугольник, следовательно, \(AB+C'D'=BC'+AD'\).
Т.к. \(BC'=BC-CC', \ AD'=AD-DD'\), то:
\[AB+C'D'=BC-CC'+AD-DD' \Rightarrow C'D'+CC'+DD'=BC+AD-AB=CD\]
Получили, что в четырехугольнике \(C'CDD'\) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, \(CD\) касается окружности.
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.
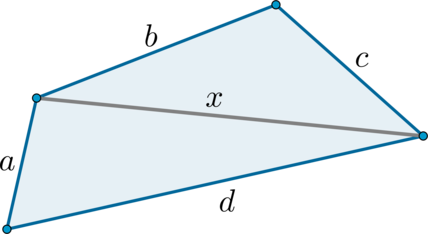
Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то \(a+x>d\) и \(b+c>x\). Складывая данные неравенства, получим: \(a+x+b+c>d+x \Rightarrow a+b+c>d\). Следовательно, сумма любых трех сторон всегда больше четвертой стороны.
Теоремы
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).
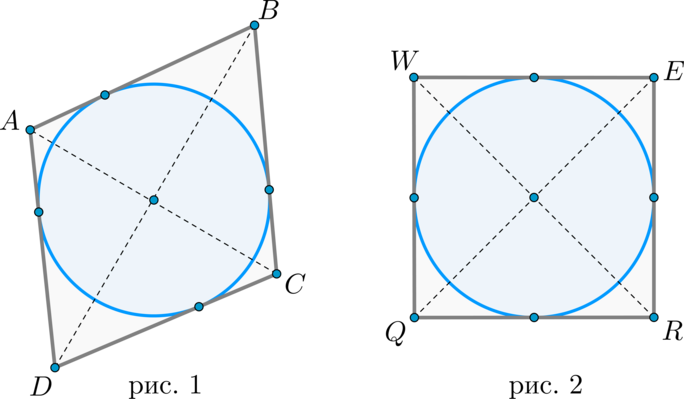
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.
Доказательство
1) Рассмотрим параллелограмм \(ABCD\), в который вписана окружность. Тогда \(AB+CD=BC+AD\). Но в параллелограмме противоположные стороны равны, т.е. \(AB=CD, \ BC=AD\). Следовательно, \(2AB=2BC\), а значит, \(AB=BC=CD=AD\), т.е. это ромб.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.
2) Рассмотрим прямоугольник \(QWER\). Т.к. прямоугольник является параллелограммом, то согласно первому пункту \(QW=WE=ER=RQ\), т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.










